20190531考试总结

第一题出锅有点惨~
拿到题后从头看了一下五道题，做题顺序基本和给出的顺序无异，不过最后一题看起来有点吓人

T1

问题描述

给出一个正整数 n，现在问存在多少个 x，使得 x在十进制下的每一位之和加上 x 等于 n。

分析

（老刘说关键在审题。。。）
言简意赅的题目描述非常讨喜，但是我看到题目就蒙了，更恐怖的是我把十进制看成了二进制，然后。。。
言归正传，这道题的解法还是很多的，你可以选择将数拆分再进行求解，更方便的你能用9重循环的暴力求解（因为是十进制每个数字都是0~9,且n<=1000000000）,注意100000000要特判，就像这样……

    if(n==1000000000)
	{ 
	 	cout<<1<<endl<<999999932<<endl;
	 	return 0;
	}
	for(int a=0;a<=9;a++)
	 for(int b=0;b<=9;b++)
	  for(int c=0;c<=9;c++)
	   for(int d=0;d<=9;d++)
	    for(int e=0;e<=9;e++)
	     for(int f=0;f<=9;f++)
	      for(int g=0;g<=9;g++)
	       for(int h=0;h<=9;h++)
	        for(int i=0;i<=9;i++)
	        {
	        	int s=a*100000000+b*10000000+c*1000000+d*100000+e*10000+f*1000+g*100+h*10+i;
	        	if(s>=n)
	        	 break;
	        	if(s+a+b+c+d+e+f+g+h+i==n)
	        	{
	        		cnt++;
	        		ans[cnt]=s;
				}
			}

考试的时候我的代码就是根据这思路写的，只不过用了结构体简化代码，结果。。只有20分，至今没有找到错误……

T2

题目描述

蓝月商城出新技能书了！！
如果古天乐想购买“旋风斩”，则他需要花费A元；如果古天乐想买“半月弯刀”，则需要B元；如果古天乐两个一起买，则需要C元。
蓝月的设计师非常有头脑，每样商品的利润都是相同的。即假设旋风斩和半月弯刀的成本为a,b元，则A-a=B-b=C-a-b。
给出A，B，C求出利润，数据保证为正数。

分析

其实这道题我考试的时候并没有完全理解，但是题目非常的良心，给出了“A-a=B-b=C-a-b”，那么其实根据这个等式结果也出来了（考试的时候我只是看了三个样例然后发现了规律……）

scanf("%d",&t);
	for(int i=1;i<=t;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		int d=a+b-c;
		printf("%d\n",d);
	}
	return 0;

理论上的高能从这里开始

T3

题目描述

古天乐在搭积木，积木图可以抽象为一个n*m的网格图，其中第(i,j)的位置有A[i][j]个积木。求表面积。
格式
输入第一行两个数n,m，接下来n行每行m个数，表示A[i][j]。
输出一个数，表示表面积。

分析

最先看到这道题我最开始以为将每行每列的最大值都求出来就可以求出四周的表面积从而求出答案，但是首先不符合样例，原因是会有重叠，当一行内有一个格子比它的前或后方高但它并不是最高的时候，就会有高起部分被遮挡，虽然这不难想到，但是考试的时候脑子就跟短路了一样。
最终考场上写出的正解是求每个格子所贡献的表面积来计算总值来计算表面总值。以a[i][j]和它的前方格子为例，如果没有任何方块和该列靠在一起，那么贡献应该是a[i][j]*4+2,被前方格子遮挡的面积为min(a[i][j],a[i+1][j]),其他方向同理，减去四个方向的遮挡就可以算出这个格子实际贡献的表面积。

#include
using namespace std;
int n,m,a[111][111],b[111][111],ans;
int main()
{
	freopen("surface.in","r",stdin);
	freopen("surface.out","w",stdout);
	scanf("%d%d",&n,&m);
	  
	for(int i=1;i<=n;i++)
	 for(int j=1;j<=m;j++)
	{
		scanf("%d",&b[i][j]);
		a[i][j]=4*b[i][j]+2;
	}
	for(int i=1;i<=n;i++)
	 for(int j=1;j<=m;j++)
	 {
	 	int left=min(b[i][j],b[i][j-1]);
	 	int right=min(b[i][j],b[i][j+1]);
	 	int qian=min(b[i][j],b[i+1][j]);
	 	int hou=min(b[i][j],b[i-1][j]);
	 	a[i][j]=a[i][j]-left-right-qian-hou;
	 	ans+=a[i][j];
	 }
	printf("%d",ans);
	return 0;
}

T4

（本场考试中最让我欣慰的题，不仅考了我比较喜欢的bfs，并且我A了）
给定一个n*n的棋盘，行和列标号为0,1,2,….,n-1。在棋盘的(i_start,j_start)位置上有一位红皇后，每次红皇后可以往六个方向走，如图所示：
现在红皇后想去(i_end,j_end)点，求最短距离，并且输出一条路径。
显然最短路径有无穷条，请按照以下顺序来搜索：UL, UR, R, LR, LL, L。
如果无解，输出Impossible

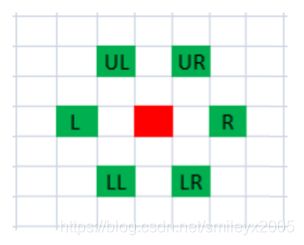
分析

（考试的时候调了半年。。。最后发现是手贱少打了逗号，没看清题目规定的搜索顺序，哎~）
搜索应该不用解释了对吧（其实最短路也没问题，只是会多做一些无用的步骤），这道题多了对搜索顺序的限制，其实这没什么关系，只要将方向数组的顺序与题目要求的顺序相对应就能满足要求，我认为这题的难点应该是输出方案，但是恰好，刘老师不久前刚说过一句话“输出顺序就只要开个数组把它是从哪个状态转移来的记录下来就行了”（原话忘了），所以我在代码中搜索的时候多记录了每一个状态的前继，最后通过递归的方式输出方案即可。

#include
using namespace std;
int n,sti,stj,edi,edj;
int dis[222][222],vis[222][222];
struct mm 
{
	int x;int y;
}pre[222][222];
int dx[6]={-2,-2,0,2,2,0};
int dy[6]={-1,1,2,1,-1,-2};
string dl[6]={"UL","UR","R","LR","LL","L"};
queue<mm>q;
void spfa()
{
	memset(dis,10,sizeof(dis));
	dis[sti][stj]=0;
	vis[sti][stj]=0;
	mm k;
	k.x=sti;
	k.y=stj;
	q.push(k);
	while(!q.empty())
	{
		k=q.front();
		q.pop();
		vis[k.x][k.y]=0;
		for(int i=0;i<=5;i++)
		{
			mm kk;
			kk.x=k.x+dx[i];
			kk.y=k.y+dy[i];
			if(kk.x<0||kk.x>=n||kk.y<0||kk.y>=n)
			 continue;
			if(dis[k.x][k.y]+1<dis[kk.x][kk.y])
			{
				dis[kk.x][kk.y]=dis[k.x][k.y]+1;
				pre[kk.x][kk.y].x=k.x;
				pre[kk.x][kk.y].y=k.y;
				if(!vis[kk.x][kk.y])
				{
					vis[kk.x][kk.y]=1;
					q.push(kk);
				}
			}
		}
	}
}
void dfs(int x,int y,int lx,int ly)
{
	if(x==0&&y==0)
	 return ;
	
	dfs(pre[x][y].x,pre[x][y].y,x,y);
	for(int i=0;i<=5;i++)
	{
		if(x+dx[i]==lx&&y+dy[i]==ly)
		{
			cout<<dl[i]<<' ';
			break;
		} 
	}
	return ;
}
int main()
{
	freopen("redqueen.in","r",stdin);
	freopen("redqueen.out","w",stdout);
	cin>>n;
	cin>>sti>>stj>>edi>>edj;
	spfa();
	if(dis[edi][edj]==168430090)
	 cout<<"Impossible"<<endl;
	else
	{
		cout<<dis[edi][edj]<<endl;
	    dfs(edi,edj,0,0);
	}
	return 0;
}

真正的高能在这里！！！

T5

（一道披着DP外皮的递推，虽然我看起来像排列组合）

题目描述

有一个长度为n的序列A，其中A[1]=1,A[n]=x，A[2…n-1]可以是1至k间任意一个正整数。求有多少个不同的序列，使得相邻两个数不同。
答案对10^9+7取模。

分析

（这题我考场上的时候没写，最后只剩一个小时不到来不及再推导数学公式）
DP版的没听懂，只理解了递推的思路，代码极其简单~~~
同时考虑两个限制条件有点困难，因此我们用两个数组来求解。设f[i]表示只满足a[1]=1的前i个数的排列种数，然后再用ans[i]表示第i个数是x的前i个数的排列数，具体讨论见代码分析

#include
using namespace std;
const long long kk=1000000007;
long long ans[111111];//表示第i个数是x的方案数
long long f[111111];//表示前i个数中a[1]=1的方案数 
int n,k,x; 
int main()
{
	freopen("construct.in","r",stdin);
	freopen("construct.out","w",stdout);
	cin>>n>>k>>x;
	f[2]=k-1;
	for(int i=3;i<=n;i++)
	 f[i]=f[i-1]*(k-1)%kk;//相邻两个不能相同，因此a[i]的位置不能填a[i-1]位置上的数字
	if(x==1)//相邻两数不相等，而a[1]必须是1，因此x==1时ans[2]为0，否则就有一种情况 
	 ans[2]=0;
	else
	 ans[2]=1; 
	for(int i=3;i<=n;i++)
	 ans[i]=(f[i-1]-ans[i-1]+kk)%kk;//前i-1个数共有f[i-1]种方案，而i-1的位置是x的有ans[i-1],又因为相邻两数不能相等，因此要减去 
	cout<<ans[n]<<endl;
	return 0;
}

最后总结：
1.暴力挺好，不要花里胡哨地化简。。。
2.在做一些简单的题的时候可以稍微慢一点，不要有手贱的错误，否则会花更多时间
3.审清题目最重要！！！
另外，DP千万别忘了初值。