Java链表
一.线性表与链表:
线性表是我们在编程里会经常用到也是必须掌握的一种数据结构,即零或多个数据元素的有限序列,我们熟知的栈,队列这些结构也可以用线性表来实现,而线性表的物理结构又分为两种:顺序存储结构和链式存储结构,对于线性表的顺序存储结构我们最直观的概念就是一维数组**(用一段地址连续的存储单元依次存储线性表的数据元素)**,而线性表的链式存储结构就是我们所要提到的链表了,其中最常用的就是单链表了,链表中每个元素包含一个称为节点的结构,其中的结点是由数据域和指针域构成的,其存储结构在物理存储单元上是非连续,非顺序的
1.5数组与单链表的比较:
数组(前三条是相对于单链表的缺点):
1)数组需要开发者自己维护下标
2)数组开辟时必须指定数组的长度,如果存放的元素过多,需要开发者自己扩容数组
3)当在数组的某些位置增加和删除元素时,还要编写代码处理元素的移动
4)时间性能:查找O(1)、插入和删除O(n)
5)空间性能:需要预分配存储空间,分大了浪费,小了容易溢出
单链表:
1)长度可变,扩展性好
2)内存利用高(可以不连续)
3)时间性能:查找O(n)、插入和删除O(1)
4)空间性能:不需要分配存储空间,只要有就可以分配,元素个数不受限制
对比可以看出数组和单链表的查找与插删时间复杂度刚好是相反的,正因为数组内存空间是连续的而且可以通过下标随机访问所以它的查找效率高,而链表内存空间不连续并且只能通过指针依次访问,所以查找效率低
相反数组内存大小是固定的,不方便动态插入删除,效率低,而链表的插入删除的效率就比较高
我们可以根据实际的需求选择合适的结构
二.链表的基本实现:
1.带头结点的单链表:
class SingleLinkedListTakedHead<E>{
protected Node<E> head;
class Node<E>{
protected E element;
protected Node<E> next;
public Node(E data){
this.element = data;
}
}
public SingleLinkedListTakedHead(){
head = new Node<>((E)new Object());
}
//头插法 head之后去添加元素
public void addHead(E data){
//创建新节点
Node<E> newNode = new Node<>(data);
//绑定新节点的next
newNode.next = head.next;
//head.next指向新节点
head.next = newNode;
}
//尾插法
public void addTail(E data){
//创建新节点
Node<E> newNode = new Node<>(data);
//遍历当前链表,找到最后一个节点
Node<E> tmp = head;
while(tmp.next != null){
tmp = tmp.next;
}
//绑定最后的一个节点的next
tmp.next = newNode;
}
public boolean delete(E data){
//head节点需要单独处理
if(head.element == data){
head = head.next;
return true;
}
//删除某一个正常节点
Node<E> tmp = head;
while(tmp.next != null){
if(tmp.next.element == data){
tmp.next = tmp.next.next;
return true;
}
tmp = tmp.next;
}
return false;
}
//返回指定位置的节点
public Node<E> findValue(int index){
if(index < 0) return null;
Node<E> tmp = head;
while(tmp.next != null && index-- > 0){
tmp = tmp.next;
}
if(index <= 0) {
return tmp;
}
return null;
}
//得到当前链表的长度
public int getLength(){
int size = 0;
Node<E> tmp = head;
while(tmp.next != null){
size++;
tmp = tmp.next;
}
return size;
}
//遍历链表
public String toString(){
StringBuilder sb = new StringBuilder();
Node<E> tmp = head;
while(tmp.next != null){
sb.append(tmp.next.element+" ");
tmp = tmp.next;
}
return sb.toString();
}
}
2.不带头结点的单链表:
class SingleLinkedList<E>{
protected Node<E> head; //永远指向第一个有效节点
//节点类
class Node<E>{
protected E element; //数据域
protected Node<E> next;//引用域,用来连接链表中的节点
public Node(E data){
this.element = data;
}
}
//添加
public void add(E data){
//创建一个新的节点
Node<E> newNode = new Node<>(data);
//分情况:空链表 head == null
if(head == null){
head = newNode;
}else{
//链表不为空,遍历至尾节点
Node<E> tmp = head;
while(tmp.next != null){
tmp = tmp.next;
}
//绑定新节点
tmp.next = newNode;
}
}
//添加一个新节点至指定位置
public boolean addPos(E data, int pos){
if(pos < 0 || pos > getLength()+1){
return false;
}
//创建新节点
Node<E> newNode = new Node<>(data);
//插入0号位置需要特殊处理
if(pos == 0){
newNode.next = head;
head = newNode;
return true;
}
//找到pos位置
Node<E> tmp = head;
for(int i=0; i<pos-1; i++){
tmp = tmp.next;
}
//tmp指向pos-1位置的节点
//绑定新节点
newNode.next = tmp.next;
tmp.next = newNode;
return true;
}
public boolean delete(E data){
//head节点需要单独处理
if(head.element == data){
head = head.next;
return true;
}
//删除某一个正常节点
Node<E> tmp = head;
while(tmp.next != null){
if(tmp.next.element == data){
tmp.next = tmp.next.next;
return true;
}
tmp = tmp.next;
}
return false;
}
public int getLength(){
int length = 0;
Node<E> tmp = head;
while(tmp != null){
length ++ ;
tmp = tmp.next;
}
return length;
}
public Node<E> getHead() {
return head;
}
public void setHead(Node<E> head) {
this.head = head;
}
public void show(){
Node<E> tmp = head;
while(tmp != null){
System.out.print(tmp.element + " ");
tmp = tmp.next;
}
System.out.println();
}
}
3.循环单链表:
即头尾相接能让指针在链表中不停的循环起来
class LoopSingleLinkedList<E>{
protected Node<E> head;
class Node<E>{
protected E element;
protected Node<E> next;
public Node(E data){
this.element = data;
}
}
public LoopSingleLinkedList(){
head = new Node((E)new Object());
head.next = head;
}
}
三.单链表经典例题:
1.逆序输出与逆置单链表:
//逆序输出单链表
public static <E> void reversePrintList(SingleLinkedList<E>.Node<E> head){
//递归终止条件
if(head == null){
return;//处理办法
}
//提取重复逻辑,缩小问题规模
reversePrintList(head.next);
System.out.println(head.element + " ");
}
//逆置单链表
public static <E> SingleLinkedList<E>.Node<E> reverseList(SingleLinkedList<E>.Node<E> head){
SingleLinkedList<E>.Node<E> current = head; //当前节点
SingleLinkedList<E>.Node<E> prev = null;//当前节点的前一个
SingleLinkedList<E>.Node<E> newHead = null;//逆置后链表的头节点
while(current != null){
//当前节点的下一个
SingleLinkedList<E>.Node<E> next = current.next;
if(next == null){
newHead = current;
}
current.next = prev;
prev = current;
current = next;
}
return newHead;
}
逆序输出当然用递归啦,简单粗暴,当函数自调到最后一层也就是头指针指向到最后一个节点,开始逐级return,从最后一个节点输出到头结点
对于逆置单链表设置cur指向当前链表的头结点,prev作为指向它的前一个节点的指针,next作为指向它后一个节点的指针,以cur节点不为空进行循环,每次循都调整cur的指向为prev,并且prev、cur、next都继续前移
2.合并两个有序的单链表,保证合并之后依然有序
public static <E extends Comparable<E>> SingleLinkedList<E>.Node<E> mergeLinkedList(
SingleLinkedList<E>.Node<E> head1, SingleLinkedList<E>.Node<E> head2){
//确定新链表的头节点
SingleLinkedList<E>.Node<E> curHead = null;
if(head1.element.compareTo(head2.element) < 0) {
curHead = head1;
head1 = head1.next;
}else{
curHead = head2;
head2 = head2.next;
}
SingleLinkedList<E>.Node<E> tmp = curHead;
while(head1 != null && head2 != null){
if(head1.element.compareTo(head2.element) < 0){
tmp.next = head1;
head1 = head1.next;
}else{
tmp.next = head2;
head2 = head2.next;
}
tmp = tmp.next;
}
if(head1 == null){
tmp.next = head2;
}
if(head2 == null){
tmp.next = head1;
}
return curHead;
}
3.不允许遍历链表, 在 pos之前插入
public static <E> boolean insertPosBefore(
SingleLinkedList<E> list,SingleLinkedList<E>.Node<E> pos, E data){
if(list.getHead() == null || pos == null) return false;
//创建新节点
SingleLinkedList<E>.Node<E> newNode = list.createNode(pos.element);
//插入新节点至pos之后
newNode.next = pos.next;
pos.next = newNode;
//改变pos位置的element为data
pos.element = data;
return true;
}
这个也是个非常值得总结,思路巧妙的题目,虽然不能遍历链表但题目所给的pos位置的参数直接是结点类型的,代表这个位置的结点我可以直接用的,拿到pos位置的结点,如果要在pos位置之前插入新的结点,那就要让pos位置的前一个节点的next引用指向这个新结点,再将这个新结点的next引用绑定到pos结点上,但在这里只能拿到pos.next也就是pos位置的下一个结点,无法获取到pos位置的前一个结点的信息的,那就索然直接在pos位置之后插入新的结点,这很容易办到,如果想要达到插入在pos位置之前的效果只需将新插入的结点的数据域与pos结点的数据域交换即可(当然要事先保存pos位置的数据域)
4.两个链表相交,输出相交节点
public static <E> SingleLinkedList<E>.Node<E> commonNode(
SingleLinkedList<E> list1, SingleLinkedList<E> list2){
if(list1.getHead() == null || list2.getHead() == null) return null;
//计算两个链表的差值
int length1 = list1.getLength();
int length2 = list2.getLength();
int lengthDif = Math.abs(length1-length2);
SingleLinkedList<E>.Node<E> longHead = list1.getHead();
SingleLinkedList<E>.Node<E> shortHead = list2.getHead();
if(length1 < length2){
longHead = list2.getHead();;
shortHead = list1.getHead();
}
//长链表先走
for(int i=0; i<lengthDif; i++){
longHead = longHead.next;
}
//两个指针同时走
while(longHead != shortHead){
longHead = longHead.next;
shortHead = shortHead.next;
}
return longHead;
}
使用栈,创建两个栈 空间复杂度 O(n) 时间复杂度O(n)
Stack<SingleLinkedList<E>.Node<E>> stack1 = new Stack<>();
Stack<SingleLinkedList<E>.Node<E>> stack2 = new Stack<>();
while(head1 != null){
stack1.push(head1);
head1 = head1.next;
}
while(head2 != null){
stack2.push(head2);
head2 = head2.next;
}
//获取栈顶元素进行比较
//比较栈顶元素,如果相等,将该元素移除,继续比较下一个栈顶
SingleLinkedList<E>.Node<E> commonNode = null;
while(stack1.peek() == stack2.peek()){
commonNode = stack1.peek();
stack1.pop();
stack2.pop();
}
return commonNode;
}
要注意,这里的链表相交不是简单的节点上的数据相等,是两条链表完全的共用后面的节点,节点在内存上的地址要完全相同。
当然还有一种更简单粗暴的方式那就是利用栈的特性,如果把链表按顺序入栈的话那么再获取栈顶元素刚好是从链表尾端开始(如果相交那就是那些公有的节点),把两条链表分别入栈,再一个一个比较栈顶元素看它们是否是相等的即可。
5.查找单链表中倒数第K个元素
public static <E> SingleLinkedList<E>.Node<E> lastK(SingleLinkedList<E>.Node<E> head, int k){
if(head == null || k<0) return null;
//控制时间复杂度为O(n),只需要遍历链表一次实现
SingleLinkedList<E>.Node<E> front = head;
SingleLinkedList<E>.Node<E> behind = head;
for(int i=0; i<k-1; i++){
if(front.next != null){
front = front.next;
}else{
return null;
}
}
while(front.next != null){
front = front.next;
behind = behind.next;
}
return behind;
}
做这个题的方法很多,但如果要效率最高,只能遍历一次,那还是用快慢指针的方法,其实在解决单链表很多问题的时候都会引入快慢指针这个理念,只要能找出问题的逻辑与指针之间的关系即可,这个问题很简单:当快指针走到链表最后一个结点的时候,慢指针恰好走到倒数第K个结点位置,用数理只是很容易知道两个指针之间相差K-1步(都从头结点出发并且每次都走一步),那就从头结点开始快指针先跑K-1步呗,然后开始同时走,快指针走到头了慢指针自然而然就走到我们想要的位置了
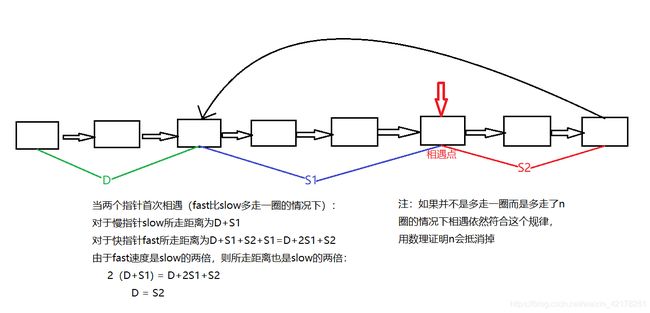
6.单链表是否有环,环的入口节点是哪个
public static <E> SingleLinkedList<E>.Node<E> ringNode(
SingleLinkedList<E>.Node<E> head){
//判断是否存在环,如果存在,则已知环中任意节点
SingleLinkedList<E>.Node<E> meeetingNode = isRing(head);
//说明环不存在
if(meeetingNode == null){
return null;
}
fast = head;
while(fast != slow){
fast = fast.next;
solw = slow.next;
}
return fast;
}
public static <E> SingleLinkedList<E>.Node<E> isRing(SingleLinkedList<E>.Node<E> head){
if(head == null) return null;
SingleLinkedList<E>.Node<E> slow = head.next;
//链表中只有一个头节点
if(slow == null) return null;
SingleLinkedList<E>.Node<E> fast = slow.next;
while(fast != null && slow != null && fast.next != null){
if(fast == slow){
return fast;
}
slow = slow.next;
fast = fast.next.next;
}
return null;
}
快慢指针的使用对这个题的求解非常有用,我们定义快指针fast每次走两步,慢指针slow每次走一步,如果链表有环,那两个指针从环的入口进入环后会一直在里面循环然后相遇,就跟我们在操场上跑步的追击问题一样,跑的快的人在多跑一圈的情况下会和跑的慢的人相遇,所以所以当快慢指针相等的时候则链表一定是有环的,当快慢指针相遇的时候就会有一个相遇点,让其中一个指针继续从相遇点开始跑,并且设立计数器记录指针跑的步数,当指针再次回到相遇点时候通过计数器就能拿到环的长度了