波仕顿房价预测的AI修正(增加去噪手段)
一、Boston方案选择与优化(增加了清洗噪声的手段)
1. 准备Boston房价数据(data为初始数据,data_new为修剪后的数据)
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import sklearn.datasets as ds
%matplotlib inline
# 创建一条直线y=ax+b
def createline(a=0,b=0,r = (0,100) , s= 100):
"""
Return y=ax+b.
r=range(x)
s=x.shape
"""
x = np.linspace(r[0] , r[1] , s)
y = a * x + b
return x,y
# remove data from DataFrame by ax+b
# d=0,remove above rows
# d=1,remove below rows
def removedata(data, column , target , a=0,b=0,d=0):
data["sub"] = data[target] - (data[column] * a + b)
if d == 0:
data["flag"] = data["sub"] < 0
else:
data["flag"] = data["sub"] > 0
data2 = data[data["flag"]]
del data2["sub"]
del data2["flag"]
return data2.copy()
boston = ds.load_boston()
targetname = "MEDV"
# 修剪噪音数据
data = pd.DataFrame(boston.data , columns = boston.feature_names)
#data = pd.read_csv('../data/housing2.data')
data[targetname] = boston.target
plt.figure(figsize=[20,5])
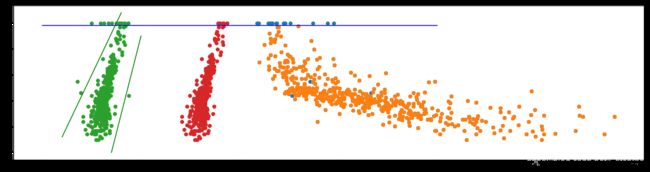
plt.scatter(data["LSTAT"] + 20 , data[targetname])
#根据观察,删除噪声数据(仅试验,不考虑删除LSTAT噪声数据)
data3 = removedata(data , "RM" , targetname , 8 , -10 , 0)
data4 = removedata(data3 , "RM" , targetname , 15 , -105 , 1)
data5 = removedata(data4 , "LSTAT" , targetname , 0 , 49 , 0)
plt.scatter(data5["LSTAT"] + 20 , data5[targetname])
data["sub"] = data[targetname] - (data["RM"] * 8 - 10)
data["sub2"] = data[targetname] - (data["RM"] * 15 - 105)
#print(data[["RM","target","sub"]])
data["flag"] = (data["sub"] < 0) & (data["sub2"] > 0)
del data["flag"]
plt.scatter(data["RM"] , data[targetname])
x,y = createline(8 , -10 , (2,8) , 100)
plt.plot(x,y , c='g')
x,y = createline(15 , -105 , (7,10))
plt.plot(x,y ,c='g' )
x,y = createline(0 , 49 , (0 , 40) , 50)
plt.plot(x,y ,c='b' )
data2 = data[(data["sub"] < 0) & (data["sub2"] > 0)]
plt.scatter(data2["RM"] + 10 , data2[targetname])
del data["sub"]
del data["sub2"]
del data2["sub"]
del data2["sub2"]
#删除列的等价函数
#1. DF= DF.drop('column_name', 1)
#2. DF.drop('column_name',axis=1, inplace=True)
#3. DF.drop([DF.columns[[0,1, 3]]], axis=1,inplace=True) # Note: zero indexed
#data_new = data2.T[0:14].T
#data = data.T[0:14].T
data_new = data2
print('feature names =' , boston.feature_names)
feature names = ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']
2.通过图形化查看所有数据与标签的关系
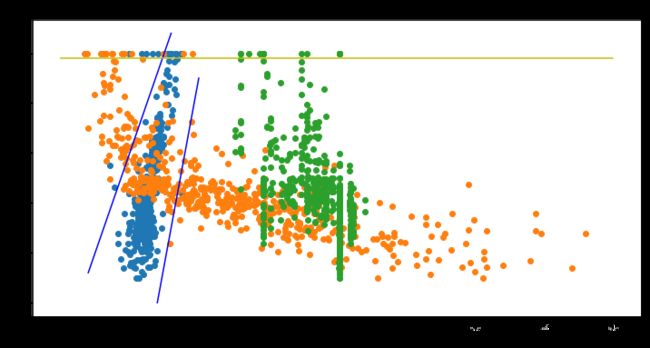
def showmodel(data , column_i):
plt.scatter(data[data.keys()[column_i]] , data.MEDV)
x_label = 'column_i=%d'%(column_i)
plt.xlabel(x_label)
plt.ylabel('MEDV')
plt.title(data.keys()[column_i] + ' - MEDV')
plt.figure(figsize=[12 , 6])
showmodel(data , 5) #RM-MEDV
showmodel(data , 12) #LSTAT-MEDV
showmodel(data , 10) #PTRADIO-MEDV
x,y = createline(8 , -10 , (2,8) , 100)
plt.plot(x,y, c='b')
x,y = createline(15 , -105 , (7,10))
plt.plot(x,y ,c='b' )
x,y = createline(0 , 49 , (0 , 40) , 50)
plt.plot(x,y ,c='y' )
[]
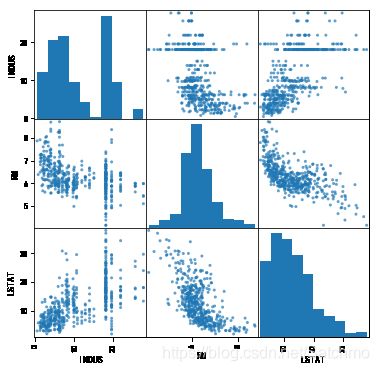
查看各个特征的散点分布
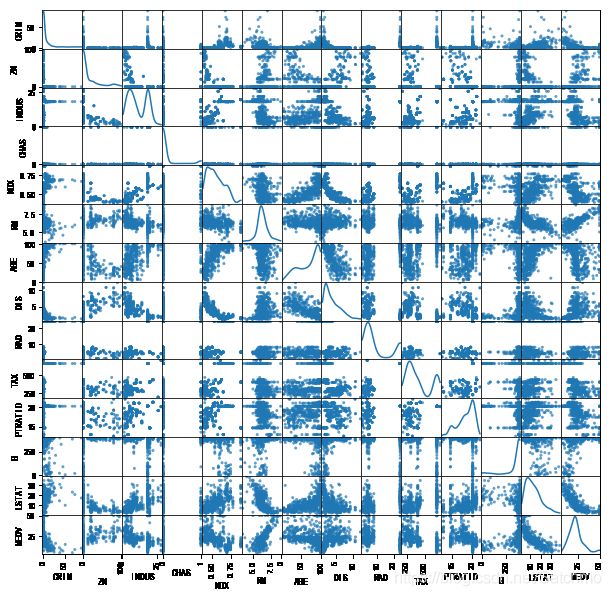
pd.plotting.scatter_matrix(data, alpha=0.7, figsize=(10,10), diagonal='kde')
pd.plotting.scatter_matrix(data_new, alpha=0.7, figsize=(10,10), diagonal='kde')
特征选择
特征维度较大,为了保证模型的高效预测,需要进行特征选择。每种特征都有自己含义和数据量级,单纯地依靠方差来判断可能效果不好,直接使用与目标变量的相关性强的变量作为最终的特征变量。
通过相关系数法进行特征选择from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
# select feature from DataFrame
def selectbest(data,k=3):
corr = data.corr()
#x = data[['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX','PTRATIO', 'B', 'LSTAT']]
#y = data[['MEDV']]
x = data[data.columns[0:data.columns.size - 1]]
y = data[data.columns[data.columns.size - 1,]]
#print('y=',y)
selectKBest = SelectKBest(f_regression, k=k)
bestFeature = selectKBest.fit_transform(x,y)
#print('SelectKBest=',SelectKBest.get_support())
return x.columns[selectKBest.get_support()]
best = selectbest(data,k=3)
best_new = selectbest(data_new,k=3)
print('best feature is' , best)
print('new best feature is', best_new)
best feature is Index(['RM', 'PTRATIO', 'LSTAT'], dtype='object') new best feature is Index(['INDUS', 'RM', 'LSTAT'], dtype='object')
- 这里我们看出和波士顿房价相关性最强的三个因素,分别是,RM(每栋住宅的房间数),PTRATIO(城镇中的教师学生比例),LSTAT(地区中有多少房东属于低收入人群)。 还是具备一定逻辑性的,首先,房子越大房价自然高(不管在哪个地域),其次,师生比与房价成反比,教育的重视,教育资源越是富裕的地方,生源就会大,师生比自然会降低,周边的房价会升高,这就是所谓的“学区房”概念吧。关于有多少房东属于低收入人群和房价的负相关关系,这个也比较好理解,各种原因吧。
- 经过降噪后,则采用INDUS(城镇非零售业用地比例)、RM(每栋住宅的房间数)、LSTAT(地区中有多少房东属于低收入人群)等三个字段,验证一下,预测效果是否有所提升。
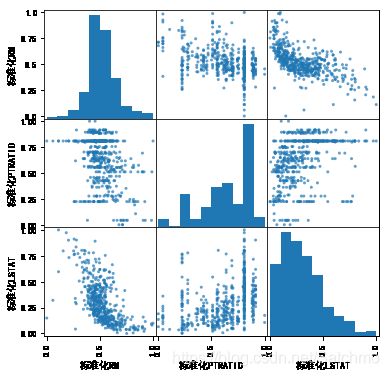
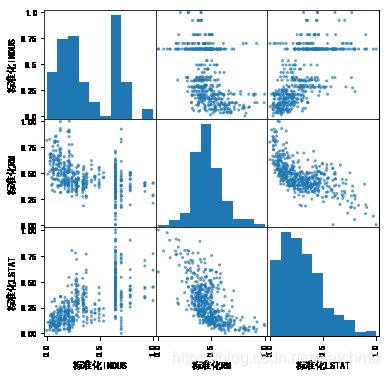
best_mix = ['RM','PTRATIO','LSTAT','INDUS'] features = data[best] features_new = data_new[best_new] features_mix = data_new[best_mix] pd.plotting.scatter_matrix(features, alpha=0.7, figsize=(6,6), diagonal='hist') pd.plotting.scatter_matrix(features_new, alpha=0.7, figsize=(6,6), diagonal='hist')
array([[, , ], [ , , ], [ , , ]], dtype=object)
特征归一化处理
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
fc = features.copy()
fc_copy = features.copy()
for feature in fc_copy.columns:
feature_std = '标准化'+feature
fc[feature_std] = scaler.fit_transform(fc[[feature]])
del fc[feature]
fc_new = features_new.copy()
fc_new_copy = features_new.copy()
for feature in fc_new_copy.columns:
feature_std = '标准化'+feature
fc_new[feature_std] = scaler.fit_transform(fc_new[[feature]])
del fc_new[feature]
#散点可视化,查看特征归一化后的数据
font={
'family':'SimHei'
}
mpl.rc('font', **font)
pd.plotting.scatter_matrix(fc, alpha=0.7, figsize=(6,6), diagonal='hist')
pd.plotting.scatter_matrix(fc_new, alpha=0.7, figsize=(6,6), diagonal='hist')
模型选择与优化
将数据拆分为训练数据及测试数据。
from sklearn.cross_validation import train_test_split x_train, x_test, y_train, y_test = train_test_split(fc, data[targetname], test_size=0.3,random_state=33) x_train_new, x_test_new, y_train_new, y_test_new = train_test_split(fc_new, data_new[targetname], test_size=0.3,random_state=33)
模型选择
采用交叉验证的方法对模型进行评估
from sklearn.model_selection import cross_val_predict from sklearn.model_selection import cross_val_score
房价预测方面,打算尝试以下方法:
- 线性回归
- 这应该是最简单也是最好理解的一种方法。
- 使用支持向量回归模型SVR
- 之前仅仅是用SVM做过一些二分类问题(SVC),这次尝试下解决回归问题。
- KNN模型
- 思路上感觉KNN可以做,但是不确定效果,可以尝试下。
- 决策树模型
- 和KNN一样,感觉是可以做,但是具体效果不太确定。
- 线性回归模型预测房价
# 1.线性回归
from sklearn import linear_model
def linear_meanscore(x_train , y_train , cv=5):
lr = linear_model.LinearRegression()
lr_predict = cross_val_predict(lr,x_train, y_train, cv=cv)
lr_y_score = cross_val_score(lr, x_train, y_train, cv=cv)
lr_meanscore = lr_y_score.mean()
return lr_predict , lr_y_score , lr_meanscore
print('columns old =',fc.columns)
print('columns new =',fc_new.columns)
print('by linear')
lr_predict , lr_y_score , lr_meanscore = linear_meanscore(x_train , y_train ,cv=3)
print('old:y_score=' , lr_y_score,'meanscore=' , lr_meanscore)
lr_predict_new , lr_y_score_new , lr_meanscore_new = linear_meanscore(x_train_new , y_train_new , cv=3)
print('new:y_score=' , lr_y_score_new,'meanscore=' , lr_meanscore_new)
# 2.SVR(尝试三种核,'linear', 'poly', 'rbf')
from sklearn.svm import SVR
def svr_meanscore(x_train , y_train , kernel = 'linear', cv=5):
linear_svr = SVR(kernel = kernel)
linear_svr_predict = cross_val_predict(linear_svr, x_train, y_train, cv=cv)
linear_svr_score = cross_val_score(linear_svr, x_train, y_train, cv=cv)
linear_svr_meanscore = linear_svr_score.mean()
return linear_svr_predict , linear_svr_score , linear_svr_meanscore
linear_svr_predict , linear_svr_score , linear_svr_meanscore = svr_meanscore(x_train , y_train , kernel='linear' , cv=3)
linear_svr_predict_new , linear_svr_score_new , linear_svr_meanscore_new = svr_meanscore(x_train_new , y_train_new , kernel='linear' , cv=3)
print('by svr linear , meanscore = ' , linear_svr_meanscore , linear_svr_meanscore_new)
poly_svr_predict , poly_svr_score , poly_svr_meanscore = svr_meanscore(x_train , y_train , kernel='poly' , cv=3)
poly_svr_predict_new , poly_svr_score_new , poly_svr_meanscore_new = svr_meanscore(x_train_new , y_train_new , kernel='poly' , cv=3)
print('by svr poly , meanscore = ' , poly_svr_meanscore , poly_svr_meanscore_new)
rbf_svr_predict , rbf_svr_score , rbf_svr_meanscore = svr_meanscore(x_train , y_train , kernel='rbf' , cv=3)
rbf_svr_predict_new , rbf_svr_score_new , rbf_svr_meanscore_new = svr_meanscore(x_train_new , y_train_new , kernel='rbf' , cv=3)
print('by svr rbf , meanscore = ' , rbf_svr_meanscore , rbf_svr_meanscore_new)
# 3.KNN模型
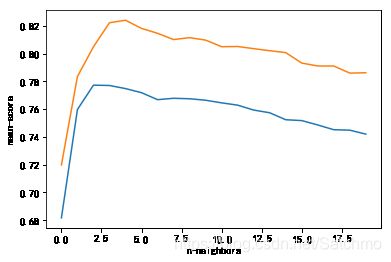
# 在KNN的回归模型当中,我们没法确定n_neighbors,因此需要最优化这个参数。
# 分别计算n_neighbors=[1,2,...,19,20]
from sklearn.neighbors import KNeighborsRegressor
def knn_meanscore(x_train , y_train , r=range(1,21) , cv=5):
score=[]
for n_neighbors in r:
knn = KNeighborsRegressor(n_neighbors, weights = 'uniform' )
knn_predict = cross_val_predict(knn, x_train, y_train, cv=cv)
knn_score = cross_val_score(knn, x_train, y_train, cv=cv)
knn_meanscore = knn_score.mean()
score.append(knn_meanscore)
plt.xlabel('n-neighbors')
plt.ylabel('mean-score')
plt.plot(score)
arr = np.array(score)
maxindex = np.where(arr == arr.max())[0][0]
return score , maxindex
score , maxindex = knn_meanscore(x_train , y_train , cv=3)
print('max score is' , np.max(score) , 'and index is', maxindex)
score_new , maxindex_new = knn_meanscore(x_train_new , y_train_new , cv=3)
print('new max score is' , np.max(score_new) , 'and index is' , maxindex_new)
columns old = Index(['标准化RM', '标准化PTRATIO', '标准化LSTAT'], dtype='object') columns new = Index(['标准化INDUS', '标准化RM', '标准化LSTAT'], dtype='object') by linear old:y_score= [ 0.73430728 0.53362851 0.72903428] meanscore= 0.665656690656 new:y_score= [ 0.67521085 0.71038091 0.77089473] meanscore= 0.718828828604 by svr linear , meanscore = 0.545647684369 0.563034847543 by svr poly , meanscore = 0.105275730495 0.0716698787245 by svr rbf , meanscore = 0.443863788545 0.476138364541 max score is 0.777201661825 and index is 2 new max score is 0.82394361143 and index is 4
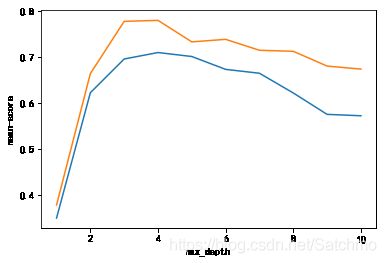
# 从上图可以发现,随着n_neighbors的逐渐增大,模型预测能力逐渐增强,但是当n_neighbors大于2以后,模型评分趋于下降。因此我们选取n_neighbors=2。
n_neighbors=2
def knn_meanscore_n(x_train , y_train , neighbors=2 , cv=5):
knn = KNeighborsRegressor(neighbors, weights = 'uniform' )
knn_predict = cross_val_predict(knn, x_train, y_train, cv=cv)
knn_score = cross_val_score(knn, x_train, y_train, cv=cv)
knn_meanscore = knn_score.mean()
return knn_score, knn_meanscore
knn_score , knn_meanscore = knn_meanscore_n(x_train , y_train , neighbors=n_neighbors , cv=3)
knn_score_new , knn_meanscore_new = knn_meanscore_n(x_train_new , y_train_new , neighbors=4 , cv=3)
print('neighbors=' , n_neighbors , ',mean-score=' , knn_meanscore , ',new mean-score=' , knn_meanscore_new)
neighbors= 2 ,mean-score= 0.759700125449 ,new mean-score= 0.822140512037
- 决策树预测房价 和KNN类似,这里没法确定决策树的深度,因此令最大深度分别是1至10。
#Decision Tree
from sklearn.tree import DecisionTreeRegressor
def dt_meanscore(x_train , y_train , r=range(1,11) , cv=5):
score=[]
for n in r:
dtr = DecisionTreeRegressor(max_depth = n)
dtr_predict = cross_val_predict(dtr, x_train, y_train, cv=cv)
dtr_score = cross_val_score(dtr, x_train, y_train, cv=cv)
dtr_meanscore = dtr_score.mean()
score.append(dtr_meanscore)
plt.plot(np.linspace(1,10,10), score)
plt.xlabel('max_depth')
plt.ylabel('mean-score')
arr = np.array(score)
maxindex = np.where(arr == arr.max())[0][0]
return score , maxindex
dtr_score , maxindex = dt_meanscore(x_train , y_train)
print('max score is' , np.max(dtr_score) , 'and index is', maxindex + 1)
dtr_score_new , maxindex_new = dt_meanscore(x_train_new , y_train_new)
print('new max score is' , np.max(dtr_score_new) , 'and index is' , maxindex_new + 1)
max score is 0.708923278648 and index is 4 new max score is 0.778810156847 and index is 4
发现当max_depth为[3, 4, 5]时,决策时模型评分处于极值的样子。 因此取max_depth为4。
n=4
def dt_meanscore_n(x_train , y_train , n=4 , cv=5):
dtr = DecisionTreeRegressor(max_depth = n)
dtr_predict = cross_val_predict(dtr, x_train, y_train, cv=cv)
dtr_score = cross_val_score(dtr, x_train, y_train, cv=cv)
dtr_meanscore = dtr_score.mean()
return dtr_score , dtr_meanscore
dtr_score , dtr_meanscore = dt_meanscore_n(x_train , y_train , n=n ,cv=3)
print('n=' , n , 'dtr meanscore is' , dtr_meanscore)
dtr_score_new , dtr_meanscore_new = dt_meanscore_n(x_train_new , y_train_new , n=3 ,cv=3)
print('n=' , 3 , 'new dtr meanscore is' , dtr_meanscore_new)
n= 4 dtr meanscore is 0.767570351249 n= 3 new dtr meanscore is 0.77836000644
模型评估
接下来,汇总下评分。
evaluating = {
'lr':lr_y_score,
'linear_svr':linear_svr_score,
'poly_svr':poly_svr_score,
'rbf_svr':rbf_svr_score,
'knn':knn_score,
'dtr':dtr_score
}
evaluating = pd.DataFrame(evaluating)
evaluating.plot.kde(alpha=1.0,figsize=(15,7))
evaluating.hist(color='k',alpha=1.0,figsize=(15,7))
evaluating_new = {
'lr':lr_y_score_new,
'linear_svr':linear_svr_score_new,
'poly_svr':poly_svr_score_new,
'rbf_svr':rbf_svr_score_new,
'knn':knn_score_new,
'dtr':dtr_score_new
}
evaluating_new = pd.DataFrame(evaluating_new)
evaluating_new.plot.kde(alpha=1.0,figsize=(15,7))
evaluating_new.hist(color='k',alpha=1.0,figsize=(15,7))
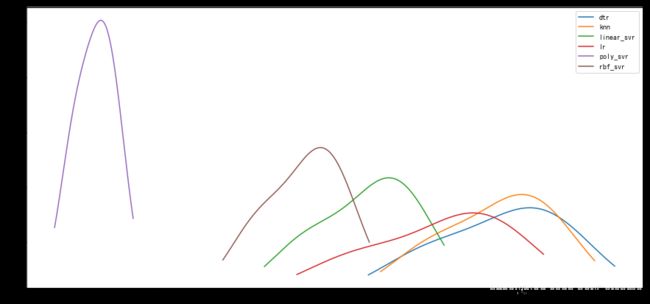
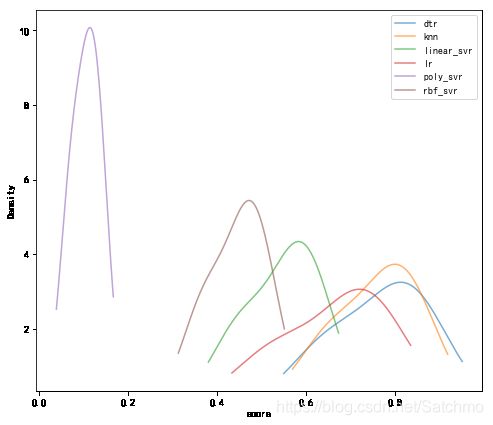
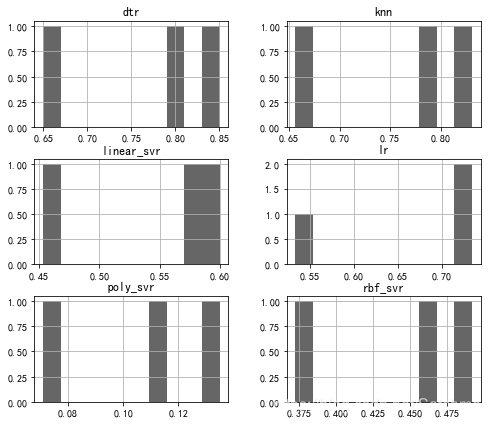
从以上两张图发现,kernerl为poly的SVR得分受数据影响明显,而且得分偏低,其他的几个模型类似linear/rbf的SVR,dtr,都呈现出相同的趋势,KNN模型应该是算是截至在现在得分最高的模型。(降噪后的其他几个参数的值也有所发散)
模型优化
接下来想想办法,看看SVR还能不能被拯救。
首先对线性核进行最优化。
线性核我们通过更改惩罚系数C来查看对模型的影响。def linear_svr_c(x_train , y_train , c=[1,10,1e2,1e3,1e4] ,cv=5):
lSVR_score=[]
for i in c:
ii = int(i)
linear_svr = SVR(kernel = 'linear', C=ii)
linear_svr_predict = cross_val_predict(linear_svr, x_train, y_train, cv=cv)
linear_svr_score = cross_val_score(linear_svr, x_train, y_train, cv=cv)
linear_svr_meanscore = linear_svr_score.mean()
lSVR_score.append(linear_svr_meanscore)
plt.plot(lSVR_score)
arr = np.array(lSVR_score)
maxindex = np.where(arr == arr.max())[0][0]
return lSVR_score,maxindex
c=[1,10,1e2,1e3,1e4]
lSVR_score , maxindex = linear_svr_c(x_train , y_train , c=c)
print('svr score is' , lSVR_score , ',max index=' , maxindex)
lSVR_score_new , maxindex_new = linear_svr_c(x_train_new , y_train_new , c=c)
print('new svr score is' , lSVR_score_new , ',max index=' , maxindex_new)
svr score is [0.56090298681915218, 0.6631724150869216, 0.66367998548720231, 0.66228115108382268, 0.66208974927596076] ,max index= 2 new svr score is [0.58595736894624917, 0.69215903959423841, 0.69852890948926805, 0.6988919799405221, 0.69889079786398545] ,max index= 3
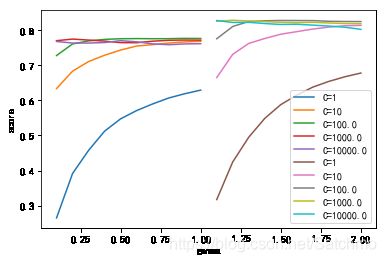
观察C为[1,10,100,1000]时对模型的影响,发现当C为10时,模型评分处于极值状态,随着C的增大,模型得分趋于稳定变化不大,因此认为C为10时模型最优。而sklearn关于线性核的默认状态C为1。
def linear_svr_cn(x_train , y_train , n=10 ,cv=cv):
linear_svr = SVR(kernel = 'linear', C=n)
linear_svr_predict = cross_val_predict(linear_svr, x_train, y_train, cv=cv)
linear_svr_score = cross_val_score(linear_svr, x_train, y_train, cv=cv)
linear_svr_meanscore = linear_svr_score.mean()
return linear_svr_meanscore
linear_svr_meanscore = linear_svr_cn(x_train , y_train , n=10)
linear_svr_meanscore_new = linear_svr_cn(x_train_new , y_train_new , n=10)
print('linear svr meanscore is' , linear_svr_meanscore , ',new score is' , linear_svr_meanscore_new)
linear svr meanscore is 0.663172415087 ,new score is 0.692159039594
'poly'核优化,通过尝试修改惩罚系数C和degree。
def poly_svr_c(x_train , y_train , c=[1,10,1e2,1e3,1e4], d=[1,2,3,4,5,6,7,8,9,10] ,cv=5):
polySVR_score=[]
for i in c:
for j in d:
poly_svr = SVR(kernel = 'poly', C=i, degree=j)
poly_svr_predict = cross_val_predict(poly_svr, x_train, y_train, cv=cv)
poly_svr_score = cross_val_score(poly_svr, x_train, y_train, cv=cv)
poly_svr_meanscore = poly_svr_score.mean()
polySVR_score.append(poly_svr_meanscore)
plt.plot(polySVR_score)
poly_svr_c(x_train , y_train , d= np.linspace(1,10,10))
从上图看出,对变量C来说,当C>10时,poly核模型得分普遍较高,当degree=2时,模型得分最高。我们查看SVR的API,发现,poly核默认的degree为3,C为1,可以从图中看出,优化后的模型得分增加不少。
def poly_svr_cd(x_train , y_train , n=1000 , d=2 ,cv=5):
poly_svr = SVR(kernel = 'poly', C=n, degree=d)
poly_svr_predict = cross_val_predict(poly_svr, x_train, y_train, cv=cv)
poly_svr_score = cross_val_score(poly_svr, x_train, y_train, cv=cv)
poly_svr_meanscore = poly_svr_score.mean()
return poly_svr_meanscore
poly_svr_meanscore = poly_svr_cd(x_train , y_train)
poly_svr_meanscore_new = poly_svr_cd(x_train_new , y_train_new)
print('poly svr meanscore is' , poly_svr_meanscore , ',new score is' , poly_svr_meanscore_new)
poly svr meanscore is 0.772448196646 ,new score is 0.828494071678
‘rbf'核优化,优化惩罚系数C和gamma。
def rbf_svr_c(x_train , y_train , c=[1,10,1e2,1e3,1e4], d=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1] ,do=1.0 ,cv=5):
for i in [1,10,1e2,1e3,1e4]:
rbfSVR_score=[]
for j in d:
rbf_svr = SVR(kernel = 'rbf', C=i, gamma=j)
rbf_svr_predict = cross_val_predict(rbf_svr, x_train, y_train, cv=cv)
rbf_svr_score = cross_val_score(rbf_svr, x_train, y_train, cv=cv)
rbf_svr_meanscore = rbf_svr_score.mean()
rbfSVR_score.append(rbf_svr_meanscore)
dd = np.array(d) + do
plt.plot(dd,rbfSVR_score,label='C='+str(i))
plt.legend()
plt.xlabel('gamma')
plt.ylabel('score')
rbf_svr_c(x_train , y_train , do=0)
rbf_svr_c(x_train_new , y_train_new , do=1)
从上图发现,gamma从0.1递增到1.0,步长为0.1,模型得分有递增的趋势,当C>=10时,gamma对模型的影响较小,当C=100时,gamma=0.5时,’rbf‘模型评分更高。
def rbf_svr_cg(x_train , y_train , n=100 , d=0.5 ,cv=5):
rbf_svr = SVR(kernel = 'rbf', C=n, gamma=d)
rbf_svr_predict = cross_val_predict(rbf_svr, x_train, y_train, cv=cv)
rbf_svr_score = cross_val_score(rbf_svr, x_train, y_train, cv=cv)
rbf_svr_meanscore = rbf_svr_score.mean()
return rbf_svr_meanscore
rbf_svr_meanscore = rbf_svr_cg(x_train , y_train)
rbf_svr_meanscore_new = rbf_svr_cg(x_train_new , y_train_new)
print('rbf score is' , rbf_svr_meanscore , ',new score is' , rbf_svr_meanscore_new)
rbf score is 0.775660090946 ,new score is 0.827778159004
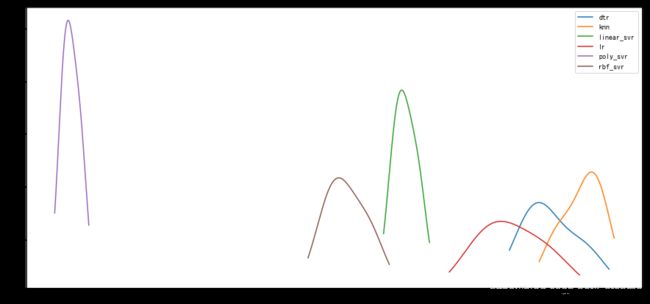
接下来,对最优化的模型进行二次归类。
#print(lr_y_score)
#print(linear_svr_score)
#print(poly_svr_score)
#print(rbf_svr_score)
#print(knn_score)
#print(dtr_score)
optimizer = {
'lr':lr_y_score,
'linear_svr':linear_svr_score,
'poly_svr':poly_svr_score,
'rbf_svr':rbf_svr_score,
'knn':knn_score,
'dtr':dtr_score
}
optimizer= pd.DataFrame(optimizer)
optimizer.plot.kde(alpha=0.6,figsize=(8,7))
plt.xlabel('score')
optimizer.hist(color='k',alpha=0.6,figsize=(8,7))
最优模型确定
对每个经过优化后的模型进行得分对比
此时发现,rbf核的SVR模型在优化后变成了最好的模型。线性核的SVR和线性回归因为策略的局限性,模型能力排在最后。
模型预测
接下来对测试数据集进行预测。
def predict_score(x_train , y_train , x_test , y_test):
#rbf
rbf_svr = SVR(kernel = 'rbf', C=100, gamma=0.5)
rbf_svr.fit(x_train,y_train)
rbf_svr_y_predict = rbf_svr.predict(x_test)
rbf_svr_y_predict_score=rbf_svr.score(x_test, y_test)
#KNN
knn.fit(x_train,y_train)
knn_y_predict = knn.predict(x_test)
knn_y_predict_score = knn.score(x_test, y_test)
#poly_svr
poly_svr = SVR(kernel = 'poly', C=1000, degree=2)
poly_svr.fit(x_train,y_train)
poly_svr_y_predict = poly_svr.predict(x_test)
poly_svr_y_predict_score = poly_svr.score(x_test, y_test)
#dtr
dtr = DecisionTreeRegressor(max_depth = 4)
dtr.fit(x_train, y_train)
dtr_y_predict = dtr.predict(x_test)
dtr_y_predict_score = dtr.score(x_test, y_test)
#lr
lr.fit(x_train, y_train)
lr_y_predict = lr.predict(x_test)
lr_y_predict_score = lr.score(x_test, y_test)
#linear_svr
linear_svr.fit(x_train, y_train)
linear_svr_y_predict = linear_svr.predict(x_test)
linear_svr_y_predict_score = linear_svr.score(x_test, y_test)
predict_score = {
'lr':lr_y_predict_score,
'linear_svr':linear_svr_y_predict_score,
'poly_svr':poly_svr_y_predict_score,
'rbf_svr':rbf_svr_y_predict_score,
'knn':knn_y_predict_score,
'dtr':dtr_y_predict_score
}
predict_score = pd.DataFrame(predict_score, index=['score']).transpose()
predict_score.sort_values(by='score',ascending = False)
return predict_score , rbf_svr_y_predict , knn_y_predict , poly_svr_y_predict , dtr_y_predict , lr_y_predict , linear_svr_y_predict
predict_score1 , rbf_svr_y_predict , knn_y_predict , poly_svr_y_predict , dtr_y_predict , lr_y_predict , linear_svr_y_predict = predict_score(x_train , y_train , x_test , y_test)
print('predict score is ')
print(predict_score1)
predict_score2 , rbf_svr_y_predict2 , knn_y_predict2 , poly_svr_y_predict2 , dtr_y_predict2 , lr_y_predict2 , linear_svr_y_predict2 = predict_score(x_train_new , y_train_new , x_test_new , y_test_new)
print('new predict score is ')
print(predict_score2)
predict score is
score
dtr 0.710227
knn 0.728427
linear_svr 0.620570
lr 0.618017
poly_svr 0.708969
rbf_svr 0.737578
new predict score is
score
dtr 0.758771
knn 0.785633
linear_svr 0.690345
lr 0.684686
poly_svr 0.847218
rbf_svr 0.842004
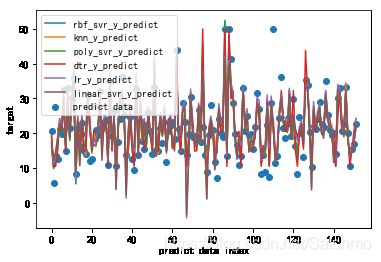
对各个模型的预测值整理
plt.scatter(np.linspace(0,151,152),y_test, label='predict data')
labelname=[
'rbf_svr_y_predict',
'knn_y_predict',
'poly_svr_y_predict',
'dtr_y_predict',
'lr_y_predict',
'linear_svr_y_predict']
y_predict={
'rbf_svr_y_predict':rbf_svr_y_predict,
'knn_y_predict':knn_y_predict,
'poly_svr_y_predict':poly_svr_y_predict,
'dtr_y_predict':dtr_y_predict,
'lr_y_predict':lr_y_predict,
'linear_svr_y_predict':linear_svr_y_predict
}
y_predict=pd.DataFrame(y_predict)
for name in labelname:
plt.plot(y_predict[name],label=name)
plt.xlabel('predict data index')
plt.ylabel('target')
plt.legend()
综合表现来看,rbf_svr的鲁棒性更强一点。
2018/09/01
关于特征选择过程的思考:在上述步骤中,通过将特征与目标变量进行相关系数并作为依据,选出三个具有强相关性的特征作为模型的输入。但是似乎忽略了弱相关变量对目标变量的影响。将在以下部分进行讨论。
各个特征之间虽然没有很强的一对一字面上理解的因果关系,但是,根据各个单一特征之间的皮尔森相关系数,尝试排除彼此有很强线性相关的变量,保证特征之间都是相互独立非线性因果的关系。这样做的目的也是为了避免多重共线性的过拟合问题。corr = data.corr()
corr_new = data_new.corr()
for column in corr.columns:
inxs = (abs(corr[column])<1) & (abs(corr[column])>0.6)
for inx in corr.index[inxs]:
print(column+'<-->'+inx)
corr['MEDV'].abs().sort_values(ascending=False)
CRIM<-->RAD ZN<-->DIS INDUS<-->NOX INDUS<-->AGE INDUS<-->DIS INDUS<-->TAX INDUS<-->LSTAT NOX<-->INDUS NOX<-->AGE NOX<-->DIS NOX<-->RAD NOX<-->TAX RM<-->LSTAT RM<-->MEDV AGE<-->INDUS AGE<-->NOX AGE<-->DIS AGE<-->LSTAT DIS<-->ZN DIS<-->INDUS DIS<-->NOX DIS<-->AGE RAD<-->CRIM RAD<-->NOX RAD<-->TAX TAX<-->INDUS TAX<-->NOX TAX<-->RAD LSTAT<-->INDUS LSTAT<-->RM LSTAT<-->AGE LSTAT<-->MEDV MEDV<-->RM MEDV<-->LSTAT
MEDV 1.000000 LSTAT 0.737663 RM 0.695360 PTRATIO 0.507787 INDUS 0.483725 TAX 0.468536 NOX 0.427321 CRIM 0.385832 RAD 0.381626 AGE 0.376955 ZN 0.360445 B 0.333461 DIS 0.249929 CHAS 0.175260 Name: MEDV, dtype: float64
. 根据各个特征与目标变量的相关系数绝对值的排名,依次对强相关的特征进行最优筛选。
. 最终获得的特征为:['LSTAT','PTRATIO','TAX','ZN','B','CHAS']
. 以上六个特征是与目标变量最相关最独立的几个特征。
. 总的特征我们在以上基础上,将其余的按照与目标变量的相关系数依次导入。['LSTAT','PTRATIO','TAX','ZN','B','CHAS','RM','INDUS','NOX','RAD','AGE','CRIM','DIS']
. 在这里,将最少特征数量设定为1,最大特征数设为已知的6,其实这也算是一种贪心算法,仅作为探索的尝试吧。
. 通过上边的结果,我们选取效果比较好的几个模型,决策树模型,knn模型,和'rbf'核的SVR模型。from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
def feature_print(data):
knn_meanscore = []
dtr_meanscore = []
rbf_svr_meanscore = []
features2 = data.copy()
for feature in data.columns:
features2['标准化'+feature] = scaler.fit_transform(data[[feature]])
new = features2[
['标准化LSTAT','标准化PTRATIO',\
'标准化TAX','标准化ZN','标准化B',\
'标准化CHAS','标准化RM',\
'标准化INDUS','标准化NOX',\
'标准化RAD','标准化AGE','标准化CRIM','标准化DIS']]
for m in range(1,14):
#print('feature num: %d\r\n' %m)
selectKBest = SelectKBest(f_regression, k=int(m))
bestFeature = selectKBest.fit_transform(new,data[targetname])
xx = new[new.columns[selectKBest.get_support()]]
#print("features' name: ", xx.columns.tolist())
x_train, x_test, y_train, y_test = train_test_split(xx,data[targetname],test_size=0.3,random_state=33)
#knn
n_neighbors=2
knn = KNeighborsRegressor(n_neighbors, weights = 'uniform' )
knn_score = cross_val_score(knn, x_train, y_train, cv=5)
knn_meanscore.append(knn_score.mean())
#Decision Tree
dtr = DecisionTreeRegressor(max_depth = 4)
dtr_score = cross_val_score(dtr, x_train, y_train, cv=5)
dtr_meanscore.append(dtr_score.mean())
#rbf
rbf_svr = SVR(kernel = 'rbf',C=100,gamma=0.5)
rbf_svr_score = cross_val_score(rbf_svr, x_train, y_train, cv=5)
rbf_svr_meanscore.append(rbf_svr_score.mean())
evaluating = {
'rbf_svr':rbf_svr_meanscore,
'knn':knn_meanscore,
'dtr':dtr_meanscore
}
evaluating = pd.DataFrame(evaluating)
evaluating.plot()
plt.xticks(evaluating.index,range(1, 13))
plt.xlabel("features' number")
plt.ylabel('Model score')
return new
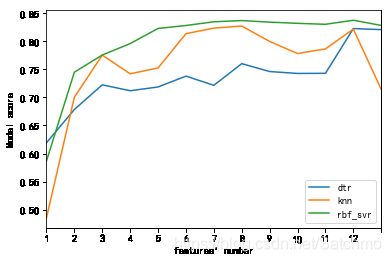
new = feature_print(data)
#feature_print(data_new)
从以上可以看出三种模型在随着排序好的特征数逐渐增加的过程中,模型得分逐渐趋于稳定。
实际相互独立的特征只有6个,我们看出,从第7个特征开始,模型的评分就趋于稳定,这和我们开始假设是吻合的,冗余的特征对于模型并没有特别的贡献。对于决策树来说,似乎特征数量愈多,模型得分越高。
对于rbf核的SVR来说,它的得分是最高的,0.83,这比之前只选取强相关的三个特征的模型得分高出10%。
接下来,我们确定特征数为6,对test数据进行预测。def feature_ok(data , new):
selectKBest = SelectKBest(f_regression, k=6)
bestFeature = selectKBest.fit_transform(new,data[targetname])
xx = new[new.columns[selectKBest.get_support()]]
print("features' name: ", xx.columns.tolist())
#knn
n_neighbors=2
knn = KNeighborsRegressor(n_neighbors, weights = 'uniform' )
knn.fit(x_train, y_train)
knn_y_predict = knn.predict(x_test)
knn_y_predict_score = knn.score(x_test, y_test)
#Decision Tree
dtr = DecisionTreeRegressor(max_depth = 4)
dtr.fit(x_train, y_train)
dtr_y_predict = dtr.predict(x_test)
dtr_y_predict_score = dtr.score(x_test, y_test)
#rbf
rbf_svr = SVR(kernel = 'rbf',C=100,gamma=0.5)
rbf_svr.fit(x_train,y_train)
rbf_svr_y_predict = rbf_svr.predict(x_test)
rbf_svr_y_predict_score=rbf_svr.score(x_test, y_test)
predict_score = {
'rbf_svr':rbf_svr_y_predict_score,
'knn':knn_y_predict_score,
'dtr':dtr_y_predict_score
}
predict_score = pd.DataFrame(predict_score, index=['score']).transpose()
predict_score.sort_values(by='score',ascending = False)
return predict_score
predict_score = feature_ok(data,new)
predict_score
features' name: ['标准化LSTAT', '标准化PTRATIO', '标准化TAX', '标准化RM', '标准化INDUS', '标准化NOX']
| score | |
|---|---|
| dtr | 0.710227 |
| knn | 0.695671 |
| rbf_svr | 0.737578 |
可以看出rbf核的SVR比之前的模型预测得分高了3%。
其实运算的时间成本上也需要考虑,这里先不写了。二、Boston房价估计(随机森林)
#!/usr/bin/python
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import ElasticNetCV
import sklearn.datasets
from pprint import pprint
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
from sklearn.metrics import f1_score
from sklearn.ensemble import RandomForestRegressor
import warnings
def not_empty(s):
return s != ''
warnings.filterwarnings(action='ignore') #忽略警告信息
np.set_printoptions(suppress=True) #设置打印选项,将输出以小数的形式呈现,默认为False,即以科学计数法
file_data = pd.read_csv('../data/housing.data', header=None) #header=None 表示原始数据中没有列索引
# a = np.array([float(s) for s in str if s != ''])
def predict_boston(file_data):
data = np.empty((len(file_data), 14))
#print(file_data) #把数据读取出来
#print(data) #形成一个以file_data 的长度为行,14为列的数组
#print(file_data.shape) #506*1的数组
#print(data.shape) #形成一个506*14的数组
#print(file_data.values)
#print(file_data.values.shape) #打印出对应的值,506*1
for i, d in enumerate(file_data.values):
#print('i=',i,'d=',d)
#print('d[0]=',list(filter(not_empty,d)))
#filter()函数接收一个函数 f 和一个list,这个函数 f 的作用是对每个元素进行判断,返回 True或 False,filter()根据判断结果自动过滤掉不符合条件的元素,返回由符合条件元素组成的新list
#首先过滤掉非空元素,然后将列表中的每个元素转换成float类型
#d = list(map(float, list(filter(not_empty, d[0].split(' ')))))
# map()是 Python 内置的高阶函数,它接收一个函数 f 和一个 list,并通过把函数 f 依次作用在 list 的每个元素上,得到一个新的 list 并返回
data[i] = d
#print('data=' ,data)
x, y = np.split(data, (13, ), axis=1) #指定进行列操作,将数据中13列进行分割,x是前13列数据,y是后面的数据
# # data = sklearn.datasets.load_boston()
# # x = np.array(data.data)
# # y = np.array(data.target)
print('样本个数:%d, 特征个数:%d' % x.shape)
print('标记列Shape:%d , %d' % y.shape)
y = y.ravel()
#构建训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=0)
"""
#Pipeline可以将许多算法模型串联起来,比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。主要带来两点好处:
#1. 直接调用fit和predict方法来对pipeline中的所有算法模型进行训练和预测。
#2. 可以结合grid search对参数进行选择开始建模...
"""
# model = Pipeline([
# ('ss', StandardScaler()),
# ('poly', PolynomialFeatures(degree=3, include_bias=True)),
# ('linear', ElasticNetCV(l1_ratio=[0.1, 0.3, 0.5, 0.7, 0.99, 1], alphas=np.logspace(-3, 2, 5),
# fit_intercept=False, max_iter=1e3, cv=3))
# ])
model = RandomForestRegressor(n_estimators=50, criterion='mse')
print('开始建模...')
model.fit(x_train, y_train)
# linear = model.get_params('linear')['linear']
# print u'超参数:', linear.alpha_
# print u'L1 ratio:', linear.l1_ratio_
# print u'系数:', linear.coef_.ravel()
#
order = y_test.argsort(axis=0)
y_test = y_test[order]
#print('y_test=')
#print(y_test)
x_test = x_test[order, :]
y_pred = model.predict(x_test)
#print('y_pred=')
#print(y_pred)
r2 = model.score(x_test, y_test)
mse = mean_squared_error(y_test, y_pred)
#f1 = f1_score(y_test , y_pred)
print('R2:', r2)
print('均方误差:', mse)
#print('f1 score=' , f1)
#
t = np.arange(len(y_pred))
mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(facecolor='w')
plt.plot(t, y_test, 'r-', lw=2, label='真实值')
plt.plot(t, y_pred, 'g-', lw=2, label='估计值')
plt.legend(loc='best') #将标签放在最好的位置,当我改为loc='upper left'时,图形出现的结果是一致的。
plt.title('波士顿房价预测', fontsize=18)
plt.xlabel('样本编号', fontsize=15)
plt.ylabel('房屋价格', fontsize=15)
plt.grid()
plt.show()
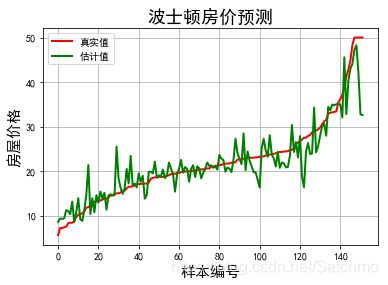
predict_boston(data)
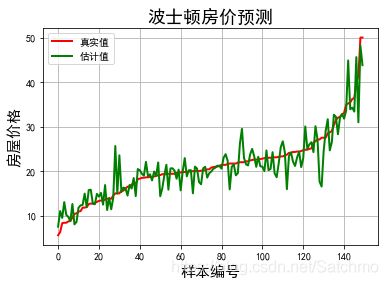
predict_boston(data_new)
样本个数:506, 特征个数:13 标记列Shape:506 , 1 开始建模... R2: 0.839296800768 均方误差: 13.3810325
样本个数:497, 特征个数:13 标记列Shape:497 , 1 开始建模... R2: 0.823018556692 均方误差: 9.56596256