测试开发基础之算法(11):二叉树的三种遍历算法及典型题解

树是一种非线性表数据结构，相比数组、链表、队列、栈、散列表等线性数据结构要复杂一些。树根据存储的数据特点，形成了很多有特点的树，比如典型的二叉树，在很多场景具有应用。二叉树在面试中也是经常会被考到的点。本篇文章就来全面认识二叉树，并学会在二叉树的各种操作。

1.树和二叉树的核心概念

用图来展示树的概念，最为直观，下面5幅图中第一个不是树，其余四个是树。

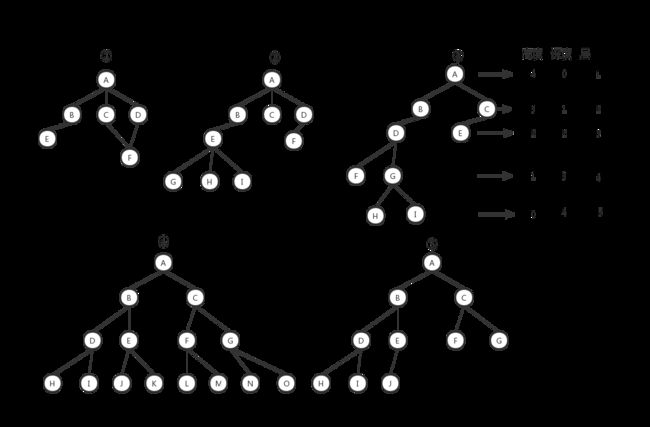
树这种数据结构很像现实生活中的树。图中的每个点，叫做“节点”，节点之间的连线叫做“父子关系”。以上面的第②个图为例，A叫根节点，A是B的父节点，B是A的子节点，B、C、D之间互称兄弟节点。G H I叫作叶子节点。

“树”还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level），上面第三幅图展示了三者之间的区别。

树的结构很多，但是常用的还是二叉树。二叉树顾名思义是只有两个叉，也就是有左右两个节点，如上面的③④⑤都是二叉树，而②是三叉树。上图第④幅图，除了叶子节点，其他节点都有两个子节点，这样的数叫做满二叉树。上图的第⑤幅图，叶子节点都落在最下面两层，最后一层的叶子节点都靠左排列，其它层节点的个数都达到了最大个数，这样的数叫做完全二叉树。

2.二叉树的存储方式

满二叉树的特点比较明显，但是完全二叉树的特点并不明显，为啥会特别提出完全二叉树的概念呢。这主要与二叉树的存储方式相关，完全二叉树的数组储存方式最省空间。下面我们详细看下二叉树的存储方式。二叉树有两种常用的存储方式：二叉链式存储法和数组顺序存储法。

• 二叉链式存储
  二叉链式存储是比较直观、常用和简单的存储法。如下图
  
  树中的每一个字段都有三个字段，分别是数据，左子节点指针和右子节点指针。从根节点开始，使用左右子节点指针，就可以遍历整个树了。

• 数组的顺序存储法

基于数组的顺序存储法，是将树中的所有结点存放到数组中。根节点存放到数组下标i=1的位置，左子节点存放到下标为2i的位置，右子节点存放下标为2i+1的位置。以下图完全二叉树为例：

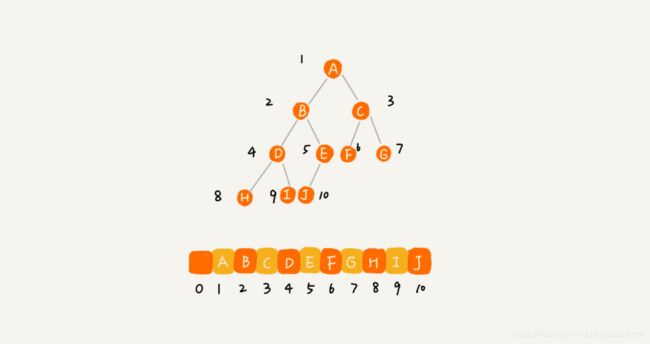
可以见完全二叉树在数组中的存储方式比较紧凑，仅浪费了一个下标为0的空间。而非完全二叉树，采用数字的顺序存储法则会浪费比较多的空间。

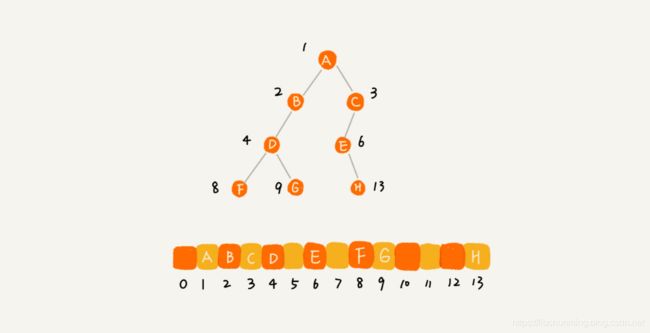
3.前中后序遍历二叉树

遍历是二叉树的重要操作，比较经典的遍历方法有：前序遍历、中序遍历和后续遍历。前中后代表是遍历时，当前节点与左右子节点的先后顺序。

• 前序遍历，指的是先打印当前节点，再打印左子树，最后打印右子树。
• 中序遍历，指的是先打印左子树，再打印当前节点，最后打印右子树。
• 后续遍历，指的是先打印左子树，再打印右子树，最后打印当前节点。

上面三种遍历方式，用图来表示就是：

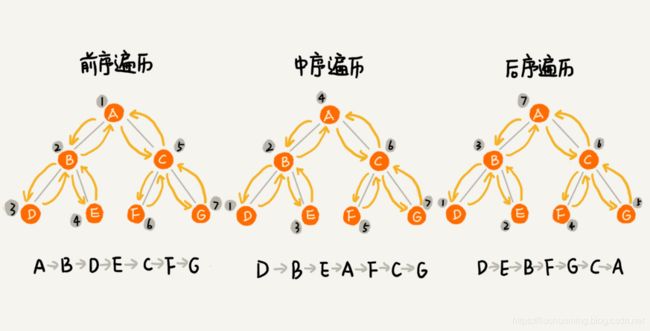
实际上，二叉树的遍历就是一个递归过程。比如前序遍历，就是先打印当前节点，接着递归打印左子树，最后递归打印右子树，遍历的时间复杂度是 O(n)。

前序遍历的递推公式：
preOrder (node) = print node->preOrder(node->left)->preOrder(node->right)

中序遍历的递推公式：
inOrder(node) = inOrder(node->left)->print node->inOrder(node->right)

后序遍历的递推公式：
postOrder(node) = postOrder(node->left)->postOrder(node->right)->print node

有了递归公式，我们看看代码的实现。

from typing import TypeVar, Generic, Optional, Generator

T = TypeVar("T")


class TreeNode(Generic[T]):
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None


def pre_order(root: Optional[TreeNode[T]]) -> Generator[T, None, None]:
    """
    :param root:根节点
    :return:生成器
    """
    if root:
        yield root.value  # 先打印当前节点
        yield from pre_order(root.left)  # 再打印左子树
        yield from pre_order(root.right)  # 再打印右子树


def in_order(root: Optional[TreeNode[T]]) -> Generator[T, None, None]:
    if root:
        yield from in_order(root.left)
        yield root.value
        yield from in_order(root.right)


def post_order(root: Optional[TreeNode[T]]) -> Generator[T, None, None]:
    if root:
        yield from post_order(root.left)
        yield from post_order(root.right)
        yield root.value


if __name__ == '__main__':
    b_tree = TreeNode("root_node")

    second_layer_left = TreeNode("second_layer_left")
    second_layer_right = TreeNode("second_layer_right")

    first = TreeNode("first")
    second = TreeNode("second")
    third = TreeNode("third")
    fourth = TreeNode("fourth")
    fifth = TreeNode("fifth")
    sixth = TreeNode("sixth")

    # 拼接成树
    b_tree.left = second_layer_left
    b_tree.right = second_layer_right

    second_layer_left.left = first
    second_layer_left.right = second

    second_layer_right.left = third
    second_layer_right.right = fourth

    first.left = fifth
    second.left = sixth

    # 前序遍历
    print(list(pre_order(b_tree)))
    # 中序遍历
    print(list(in_order(b_tree)))
    # 后续遍历
    print(list(post_order(b_tree)))

4.按层遍历二叉树

按层次遍历二叉树，就是即逐层地从左到右访问所有节点。

例如：
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal
采用递归方法，先处理一层，然后递归处理下一层，最终输出一个包含所有节点的列表。

def layer_order(root: Optional[TreeNode[T]]) -> list:
    layers = []  # 输出结果列表

    def layer_order_dfs(node, layer):
        if not node:  # 递归终止条件
            return layers

        # 处理当前层
        if len(layers) <= layer:  # 当前节点所在层大于等于输出列表长度时，给当前节点所在层新创建一个列表
            layers.append([])
        layers[layer].append(node.value)  # 当前节点加入当前层的列表中

        # 递归处理下一层
        layer_order_dfs(node.left, layer + 1)
        layer_order_dfs(node.right, layer + 1)

    layer_order_dfs(root, 0)  # 从第1层开始处理
    return layers

5.练习题：求二叉树最大最小深度

题目类似https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

本文的第一小节介绍了树的高度和深度概念，它们都是从0开始计数，只是高度从叶子节点层开始计数，深度从根节点所在层开始计数。
题目要求的最大深度表示从根节点到最近叶子节点的最长路径上的节点数量。
题目要求的最小深度表示从根节点到最近叶子节点的最短路径上的节点数量。

每个节点的深度与它左右子树的深度有关，且最大深度等于其左右子树最大深度值加上 1。
用递归公式表示，可以写作：
max_depth(node) = max(max_depth(node.left), max_depth(node.right)) + 1

当输入的节点为空节点时，我们无需继续计算其子树的深度，此时可以直接结束递归函数，并返回空节点的深度为 0。因此递归的终止条件是：

 if node is None:
    return 0

有了递归公式，和终止条件，代码就比较容易写了：

def max_depth(node: Optional[TreeNode[T]]) -> int:
    if node is None:  # 当输入的节点为空节点时，我们无需继续计算其子树的深度，直接返回0，结束递归函数
        return 0
    if node.right is None:  # 当前节点不为空，但是右子树为空，直接返回左子树的最大深度
        return max_depth(node.left) + 1
    if node.left is None:  # 当前结点不为空，右子树不为空，但是左子树为空，直接返回右子树的最大深度
        return max_depth(node.right) + 1
    # 当前节点不为空，左右子节点也不为空，返回左右子树最大深度
    return max(max_depth(node.left), max_depth(node.right)) + 1 

完整解答请参考：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/solution/tu-jie-104-er-cha-shu-de-zui-da-shen-du-di-gui-pyt/

与求最大深度类似，求最小深度也可以采用递归办法。直接上代码：

def min_depth(node: Optional[TreeNode[T]]) -> int:
    if node is None:
        return 0
    if node.left is None:
        return min_depth(node.right) + 1
    if node.right is None:
        return min_depth(node.left) + 1
    return min(min_depth(node.left), min_depth(node.right)) + 1

因为每个节点都需要被访问一次，因此时间复杂度为 O(n)。对于空间复杂度，主要考虑到递归时调用栈的空间情况。
最坏情况：树完全不平衡。例如每个节点都只有右节点或者左节点，此时将递归 n 次，需要保持调用栈的存储为 O(n)。
最好情况：树完全平衡。即树的高度为 log(n)，此时空间复杂度为 O(log(n))