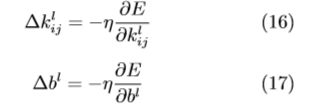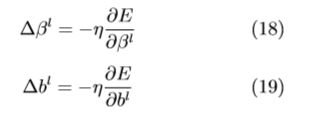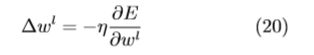卷积神经网络(CNN)探究
卷积神经网络(CNN)探究
- 1、CNN介绍
- 1.1 卷积层简谈
- 1.2池化层简谈
- 1.3全连接层简谈
- 2、CNN原理剖析
- 2.1 网络结构
- 2.1.1 卷积层
- 2.1.2 池化层
- 2.1.3 全连接层
- 2.2 反向传播算法
- 2.2.1 卷积层
- 2.2.2 池化层
- 2.2.3 全连接层
- 2.2.4 网络参数的更新过程
- 3、CNN网络实例
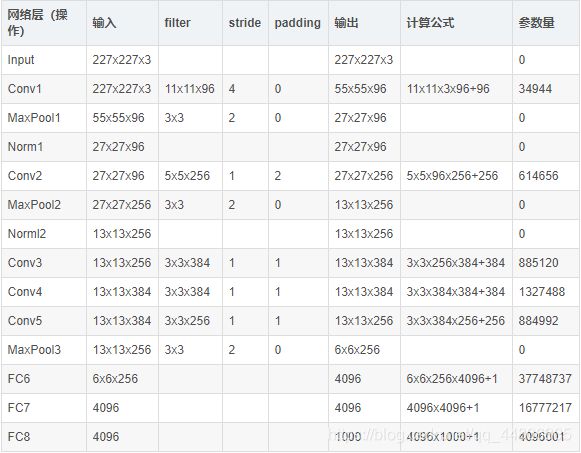
- 3.1 部分代表性CNN网络结构介绍
- 3.2 部分具有代表性的图像分类和物体检测CNN模型对比
- 4、CNN实现mnist数据集的分类
- 4.1 使用CNN模型的结构介绍
- 4.2 代码实现
- 文献参考
1、CNN介绍
CNN的基本结构由输入层、卷积层、池化层(取样层)、全连接层及输出层构成。卷积层和池化层一般会取若干个,采用卷积层和池化层交替设置,即一个卷积层连接一个池化层,池化层之后再连接一个卷积层,一次类推。由于卷积层中输出特征面的每个神经元与其输入进行局部连接,并通过对应的连接权值与局部输入进行加权求和再加偏置项,得到该神经元的输出值,该过程等同于卷积过程,卷积神经网络也由此而得名。

1.1 卷积层简谈
卷积层(convolutional layer)由多个特征面(feature map)组成,每个特征面由多个神经元(人工神经网络基本处理单位)组成,它的每个神经元通过卷积核(一种多维的权值矩阵)与上一层特征面的局部区域相连。CNN的卷积层通过卷积操作提取输入的不同特征。多层的卷积将会使特征逐步高度抽象,并被高层的卷积层所提取。如前面所说,卷积层的每个神经元通过一组权值被连接到上一层特征面的局部区域,该局部加权和通常会传递给一个非线性函数如relu函数、tanh函数等,这些非线性函数被称作激活函数。在同一个输入特征面和同一个输出特征面中,CNN的权值共享,权值共享基于一个合理的假设,即如果一个特征在计算某个空间位置时候是有用的,那么它在计算另一个位置时也应是游泳的。基于这个假设,权值共享可以显著的减少参数量。
1.2池化层简谈
池化层(pooling layer)紧跟在卷积层之后,同样由多个特征面组成,它的每一个特征面唯一对应于其上一层的一个特征面,不会改变特征面的个数(即不会改变上一层的深度),通常会周期性的加在卷积层后面。池化层起到二次提取特征、减小神经网络数据体空间尺寸的作用,常用的池化方法有最大池化(max pooling)即取局部接受域中值最大的点、均值池化(mean pooling)即对局部接受域中所有值求均值、随机池化(stachastic pooling)等,池化操作通常会由一个取样核在上一层按照特定步长滑动计算来完成。
1.3全连接层简谈
在CNN结构中,经过多个卷积层和池化层之后,连接着一个或多个全连接层。全连接层的每个神经元与其前一层的所有神经元进行全连接。全连接层可以整合卷积层和池化层中具有类别区分性的局部信息。最后一层全连接层的输出值将被传递给输出层,用以最后的分类。
2、CNN原理剖析
2.1 网络结构
2.1.1 卷积层
在卷积层,上一层的特征图被一个可学习的卷积核进行卷积,然后通过一个激活函数就可以得到输出特征图。每个输出特征图可以组合卷积多个特征图的值:
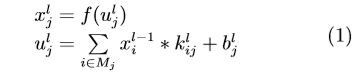
其中, ulj 称为卷积层 l 的第 j 个通道的净激活 (Net activation), 它通过对前一层输出特征图 xlj进行 卷积求和与偏置后得到的,xlj是卷积层 l 的第 j 个 通道的输出. f(·) 称为激活函数,通常可使用 relu 和 tanh 等函数. Mj 表示用于计算 ulj的输入 特征图子集,klij 是卷积核矩阵, blj是对卷积后特征 图的偏置。对于一个输出特征图 xlj,每个输入特征图 xl-1j对应的卷积核 klij 可能不同,“*”是卷积符号。
2.1.2 池化层
池化层将每个输入特征图通过下面的公式计算输出特征图:
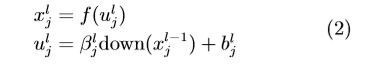
其中, ulj 称为下池化层 l 的第 j 通道的净激活,它 由前一层输出特征图 xl-1j 进行下采样加权、偏置后 得到,β 是下池化层的权重系数, blj 是下池化层的偏 置项.。符号 down(·) 表示下池化函数,它通过对输入 特征图 xl-1j 通过滑动窗口方法划分为多个不重叠的 n×n 图像块,然后对每个图像块内的像素求和、求 均值或最大值,于是输出图像在两个维度上都缩小 了 n 倍。
2.1.3 全连接层
在全连接网络中,将所有二维图像的特征图拼接为一维特征座位全连接网络的输入。全连接层l的输出可通过对输入加权求和并通过激活函数得到:
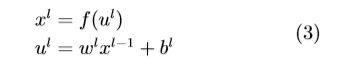
其中ul称为全连接层l 的净激活,它由前一层输出 特征图 xl−1 进行加权和偏置后得到的。wl 是全连 接网络的权重系数,bl 是全连接层 l 的偏置项。
2.2 反向传播算法
反向传播传播算法是神经网络有监督学习中的一种常用方法,其目标是根据训练样本和期望输出来估计网络参数,对于卷积神经网络而言,主要优化卷积核参数k、池化层网络权重 β、全连接层网络权 重 w 和各层的偏置参数 b 等。反向传播算法的本质 在于允许我们对每个网络层计算有效误差,并由此 推导出一个网络参数的学习规则,使得实际网络输 出更加接近目标值。
我们以平方误差损失函数的多分类问题为例介 绍反向传播算法的思路。考虑一个多分类问题的训 练总误差,定义为输出端的期望输出值和实际输出 值的差的平方:

其中,tn是第 n 个样本的类别标签真值,yn 是第 n 个样本通过前向传播网络预测输出的类别标签。对 于多分类问题,输出类别标签常用一维向量表示,即 输入样本对应的类别标签维度为正数,输出类别标 签的其他维为 0 或负数,这取决于选择的激活函数 类型,当激活函数选为 relu, 输出标签为 0,当激 活函数为 tanh, 输出标签为−1。
反向传播算法主要基于梯度下降方法,网络参 数首先被初始化为随机值, 然后通过梯度下降法向 训练误差减小的方向调整。接下来,我们以多个 “卷 积层–池化层” 连接多个全连接层的卷积神经网络 为例介绍反向传播算法。首 先 介 绍 网 络 第 l 层 的 灵 敏 度 (Sensitivity):

其中,δl 描述了总误差 E 怎样随着净激活 ul 而变 化。反向传播算法实际上通过所有网络层的灵敏度建立总误差对所有网络参数的偏导数,从而得到使 得训练误差减小的方向。
2.2.1 卷积层
为计算卷积层 l 的灵敏度, 需要用下一层下池化层 l +1 的灵敏度表示卷积层 l 的灵敏度, 然后计 算总误差 E 对卷积层参数 (卷积核参数 k、偏置参 数 b) 的偏导数。由于下池化层的灵敏度尺寸小于卷积层的灵敏 度尺寸,因此需要将下池化层 l +1 的灵敏度上池化 到卷积层 l 的灵敏度大小,然后将第 l 层净激活的激 活函数偏导与从第 l + 1 层的上池化得到的灵敏度 逐项相乘。分别由式 (1) 和 (2),通过链式求导可得 第 l 层中第 j 个通道的灵敏度:
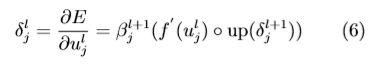
其中,up(·) 表示一个上池化操作,符号◦ 表示每个 元素相乘。若下池化因子为 n, 则 up(·) 将每个像素 在水平和垂直方向上复制 n 次,于是就可以从 l +1 层的灵敏度上池化成卷积层 l 的灵敏度大小。 函数 up(·) 可以用 Kronecker 乘积 up(x)≡ x⊗1n×n 来 实现。
然后,使用灵敏度对卷积层 l 中的参数计算偏 导。对于总误差 E 对偏移量 bl j 的偏导,可以对卷积 层 l 的灵敏度中所有节点进行求和来计算:

其中, (pi l−1)u,v 是在计算 xl j时,与 kl ij逐元素相乘 的 xl-1 i 元素。
2.2.2 池化层
&emsp: 为计算下池化层 l 的灵敏度,需要用下一层卷 积层 l +1 的灵敏度表示下池化层 l 的灵敏度,然后 计算总误差 E 对下池化参数权重系数 β、偏置参数 b 的偏导数。为计算我们需要下池化层 l 的灵敏度,我们必 须找到当前层的灵敏度与下一层的灵敏度的对应点,这样才能对灵敏度 δ 进行递推。另外,需要乘以输入 特征图与输出特征图之间的连接权值, 这个权值实 际上就是卷积核的参数。 分别由式 (1) 和 (2),通过 链式求导可得第 l 层第 j 个通道的灵敏度:
![]()
其中,对卷积核旋转 180 度使用卷积函数计算互相关,对卷积边 界进行补零处理.。
然后, 总误差对偏移量 b 的偏导与前面卷积层 的一样,只要对灵敏度中所有元素的灵敏度求和即 可:
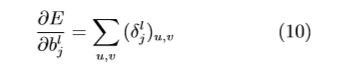
对于下采样权重 β, 我们先定义下采样算子
dl j = down(xl−1 j ),然后可通过下面的公式计算总误 差 E 对 β 的偏导::
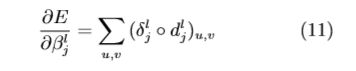
这里我们假定下采样层的下一层为卷积层,如 果下一层为全连接层,也可以做类似的推导。
2.2.3 全连接层
全连接层 l 的灵敏度可通过下式计算:
![]()
输入层的神经元灵敏度可由下面的公式计算:
![]()
总误差对偏移项的偏导如下:

接下来可以对每个神经元运用灵敏度进行权值更新。对一个给定的全连接层l,权值更新方向可用该层的输入xl-1和灵敏度 δl 的内积来表示:

2.2.4 网络参数的更新过程
卷积层参数可用下式子更新:
3、CNN网络实例
3.1 部分代表性CNN网络结构介绍
3.2 部分具有代表性的图像分类和物体检测CNN模型对比
| 网络模型 | 输入 | 优点 | 缺点 |
|---|---|---|---|
| AlexNet | 整张图像(需要对图像缩放到固定大小) | 网络简单易于训练,对图像分类有较强的鉴别力 | 网络输入要求固定大小,容易破坏物体的纵横比和上下文信息 |
| GoogLeNet | 整张图像(需要对图像缩放到固定大小) | 对图像分类拥有非常强的鉴别力,参数相对AlexNet较少 | 网络复杂,对样本数量要求较高,训练耗时 |
| VGG | 整张图像(需要对图像缩放到固定大小) | 对图像分类拥有非常强的鉴别力 | 网络复杂,对样本数量要求过高,训练耗时,需要多次对网络参数微调 |
| DPM | 整张图像 | 对物体的检测具有较强的鉴别力,对形变和遮挡具有一定的处理能力 | 使用人工设计的HOG特征;对物体检测的精度通常比本表中其他的CNN网络低 |
| R-CNN | 图像区域 | 对物体检测拥有很强的鉴别力;使用包围盒回归(Bounding box regression)提高物体的定位精度 | 依赖于区域选择算法,网络输入图像要求固定大小,容易破坏物体的纵横比和上下文信息,训练是多阶段过程;在特定检测数据集上对网络参数进行微调、提取特征、训练 SVM (Support vector machine) 分类器、包围盒回归 (Bounding box regression); 训练时间耗时、 耗存储空间 |
| SPP-net | 整张图像(不要求固定大小) | 对物体检测拥有很强的鉴别力, 输入图像可以任意大小, 可保证图像的比例信息训练速度比 R-CNN 快 3 倍左右, 测试比 R-CNN快 10∼100 倍 | 网络结构复杂时, 池化对图像造成一定的信息丢失; SPP 层前的卷积层不能进行网络参数更新; 训练是多阶段过程: 在特定检测数据集上对网络参数进行微调、提取特征、训练 SVM 分类器、包围盒回归; 训练时间耗时、 耗存储空间 |
| Fast R-CNN | 整张图像(不要求固定大小) | 训练和测试都明显快于 SPP-net (除了候选区域提取以外的环节接近于实时), 对物体检 测拥有很强的鉴别力, 输入图像可以任意大 小, 保证图像比例信息, 同时进行分类与定位 | 依赖于候选区域选择, 它仍是计算瓶颈 |
| Faster R-CNN | 整张图像(不要求固定大小) | 比 Fast R-CNN 更加快速, 对物体检测拥有很强的鉴别力; 不依赖于区域选择算法; 输入 间; 难以解决被遮挡物体的识别问题图 像可以任意大小, 保证图像比例信息, 同时 进行区域选择算法、分类与定位 | 训练过程较复杂; 计算流程仍有较大优化空 |
4、CNN实现mnist数据集的分类
4.1 使用CNN模型的结构介绍
| 网络层(操作) | 输入 | filter | stride | padding | 输出 | 参数计算 | 参数量 |
|---|---|---|---|---|---|---|---|
| input | 28x28x1 | 28x28x1 | 0 | ||||
| Conv1_1 | 28x28x1 | 3x3x16 | 1 | 0 | 28x28x16 | 3x3x1x16+16 | 160 |
| Conv1_2 | 28x28x16 | 3x3x16 | 1 | 0 | 28x28x16 | 3x3x1x16+16 | 160 |
| MaxPool1 | 28x28x16 | 2x2 | 2 | 0 | 14x14x16 | 0 | |
| Conv2_1 | 14x14x16 | 5x5x32 | 1 | 0 | 14x14x32 | 5x5x1x32+32 | 832 |
| Conv2_2 | 14x14x32 | 5x5x32 | 1 | 0 | 14x14x32 | 5x5x1x32+32 | 832 |
| MaxPool2 | 14x14x32 | 2x2 | 2 | 0 | 7x7x32 | 0 | |
| FC1 | 7x7x32 | 1000 | 7x7x32x1000+1000 | 1569000 | |||
| FC2 | 1000 | 10 | 1000x10+10 | 10010 |
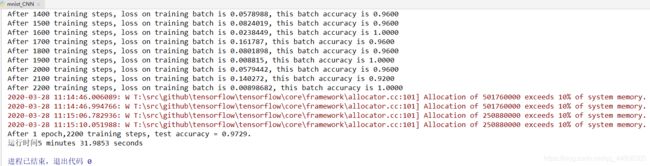
4.2 代码实现
运行环境windows10 + python3.6 + tensorflow1.8.0
# coding:utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
import os
import time
IMAGE_SIZE = 28
NUM_CHANNELS = 1
CONV1_1_SIZE = 3
CONV1_1_KERNEL_NUM = 16
CONV1_2_SIZE = 3
CONV1_2_KERNEL_NUM = 16
CONV2_1_SIZE = 5
CONV2_1_KERNEL_NUM = 32
CONV2_2_SIZE = 5
CONV2_2_KERNEL_NUM = 32
FC_SIZE = 1000
OUTPUT_NODE = 10
BATCH_SIZE = 25
LEARNING_RATE_BASE = 0.01
LEARNING_RATE_DECAY = 0.96
epoch = 1
MOVING_AVERAGE_DECAY = 0.99
MODEL_SAVE_PATH="./model/"
MODEL_NAME="mnist_model"
def get_weight(shape):
w = tf.Variable(tf.truncated_normal(shape, stddev=0.1))
return w
def get_bias(shape):
b = tf.Variable(tf.zeros(shape))
return b
def conv2d(x, w):
return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
def forward(x):
conv1_1_w = get_weight([CONV1_1_SIZE, CONV1_1_SIZE, NUM_CHANNELS, CONV1_1_KERNEL_NUM])
conv1_1_b = get_bias([CONV1_1_KERNEL_NUM])
conv1_1 = conv2d(x, conv1_1_w)
# 采用relu激活函数
relu1_1 = tf.nn.relu(tf.nn.bias_add(conv1_1, conv1_1_b))
conv1_2_w = get_weight([CONV1_2_SIZE, CONV1_2_SIZE, CONV1_1_KERNEL_NUM, CONV1_2_KERNEL_NUM])
conv1_2_b = get_bias([CONV1_2_KERNEL_NUM])
conv1_2 = conv2d(relu1_1, conv1_2_w)
relu1_2 = tf.nn.relu(tf.nn.bias_add(conv1_2, conv1_2_b))
pool1 = max_pool_2x2(relu1_2)
conv2_1_w = get_weight([CONV2_1_SIZE, CONV2_1_SIZE, CONV1_2_KERNEL_NUM, CONV2_1_KERNEL_NUM])
conv2_1_b = get_bias([CONV2_1_KERNEL_NUM])
conv2_1 = conv2d(pool1, conv2_1_w)
relu2_1 = tf.nn.relu(tf.nn.bias_add(conv2_1, conv2_1_b))
conv2_2_w = get_weight([CONV2_2_SIZE, CONV2_2_SIZE, CONV2_1_KERNEL_NUM, CONV2_2_KERNEL_NUM])
conv2_2_b = get_bias([CONV2_2_KERNEL_NUM])
conv2_2 = conv2d(relu2_1, conv2_2_w)
relu2_2 = tf.nn.relu(tf.nn.bias_add(conv2_2, conv2_2_b))
pool2 = max_pool_2x2(relu2_2)
pool_shape = pool2.get_shape().as_list()
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
reshaped = tf.reshape(pool2, [pool_shape[0], nodes])
fc1_w = get_weight([nodes, FC_SIZE])
fc1_b = get_bias([FC_SIZE])
fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_w) + fc1_b)
fc2_w = get_weight([FC_SIZE, OUTPUT_NODE])
fc2_b = get_bias([OUTPUT_NODE])
y = tf.matmul(fc1, fc2_w) + fc2_b
return y
def from_tensor_slices(x,y,batch):
r = []
for i in range(batch,len(y)+1,batch):
tumple=(x[i-batch:i],y[i-batch:i])
r.append(tumple)
return r
def backward():
x = tf.placeholder(tf.float32,[BATCH_SIZE,IMAGE_SIZE * IMAGE_SIZE * NUM_CHANNELS])
x_image= tf.reshape(x, [-1, IMAGE_SIZE, IMAGE_SIZE, NUM_CHANNELS])
y_ = tf.placeholder(tf.float32,[None, OUTPUT_NODE])
y = forward(x_image)
global_step = tf.Variable(0, trainable=False)
# 函数tf.ragmax(张量名,axis=操作轴)返回特定张量指定维度最大值的索引号,用法:tf.argmax
# 函数tf.reduce_mean(张量名,axis=操作轴)返回特定张量指定维度的平均值
# 交叉熵损失函数
ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_,1))
loss = tf.reduce_mean(ce)
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE,
global_step,
mnist.train.num_examples/ BATCH_SIZE,
LEARNING_RATE_DECAY,
staircase=True)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)
ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
ema_op = ema.apply(tf.trainable_variables())
with tf.control_dependencies([train_step,ema_op]):
train_op = tf.no_op(name='train')
saver = tf.train.Saver()
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
ckpt = tf.train.get_checkpoint_state(MODEL_SAVE_PATH)
if ckpt and ckpt.model_checkpoint_path:
saver.restore(sess,ckpt.model_checkpoint_path)
train_image, train_label = mnist.train.images, mnist.train.labels
# 实现训练集batch级图片与标签的配对
# train_db = tf.data.Dataset.from_tensor_slices((train_image, train_label)).batch(BATCH_SIZE)
train_db = from_tensor_slices(train_image, train_label,BATCH_SIZE)
# batch = mnist.train.next_batch(BATCH_SIZE)
for i in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for index, (x_train, y_train) in enumerate(train_db): # batch级别的循环
_, loss_value, step, acc = sess.run([train_op, loss, global_step,accuracy], feed_dict={x: x_train, y_: y_train})
if step % 100 == 0:
print("After %d training steps, loss on training batch is %g, this batch accuracy is %.4f"%(step, loss_value,acc))
saver.save(sess,os.path.join(MODEL_SAVE_PATH, MODEL_NAME),global_step=global_step)
def test():
with tf.Graph().as_default() as g:
images_test, labels_test = mnist.test.images, mnist.test.labels
# 随机选取1000张进行准确率测试
# idx = np.random.choice(mnist.test.num_examples,size=1000,replace=False)
# xs = images_test[idx, :]
# ys = labels_test[idx, :]
x = tf.placeholder(tf.float32,[len(images_test),IMAGE_SIZE * IMAGE_SIZE * NUM_CHANNELS])
x_image= tf.reshape(x, [-1, IMAGE_SIZE, IMAGE_SIZE, NUM_CHANNELS])
y_ = tf.placeholder(tf.float32,[None,OUTPUT_NODE])
y = forward(x_image)
saver = tf.train.Saver()
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
ckpt = tf.train.get_checkpoint_state(MODEL_SAVE_PATH)
if ckpt and ckpt.model_checkpoint_path:
# 加载训练好的模型参数
saver.restore(sess, ckpt.model_checkpoint_path)
global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
accuracy_score = sess.run(accuracy, feed_dict={x:xs, y_:ys})
print("After %s training steps, test accuracy = %g."%(global_step,accuracy_score))
else:
print("No checkpoint file found.")
if __name__ == '__main__':
# 加载数据集,由于网络原因,多数情况下自动创建数据集会失败,可手动创建MNIST_data文件夹,
# 并把mnist的四个数据集压缩包下载到此文件夹
start_time = time.time()
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
backward()
test()
end_time = time.time()
time_cost = end_time-start_time
print("运行时间%d minutes %g seconds"%(int((time_cost-time_cost%60)/60),time_cost%60))
文献参考
-[1] ZHOU Fei-Yan, JIN Lin-Peng, DONG Jun, Review of Convolutional Neural Network, 2017,Vol.40,Online Publishing No.7
-[2]常亮, 邓小明, 周明全, 武仲科, 袁野, 杨硕, 王宏安. 图像理解中的卷积神经网络. 自动化学报, 2016, 42(9): 1300−1312