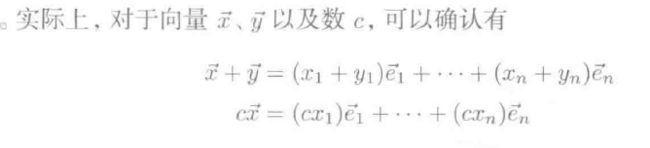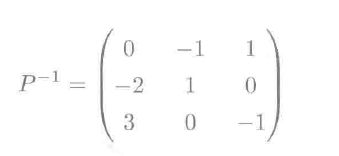读(程序员的数学 3 线性代数)-记录
目录
第一章:用空间的语言表达向量、矩阵和行列式
(向量,矩阵性质以及运算,行列式性质以及运算)
第二章:秩、逆矩阵、线性方程组(溯因原理)
(初等行变换解线性方程组、逆矩阵、秩,以及逆矩阵和相关不相关问题)
第三章:特征值、对角化
(对角化介绍,求解特征值、特征向量、可逆的特征矩阵)
第一章:用空间的语言表达向量、矩阵和行列式
1.向量
列向量:
向量的运算:(加法和乘法就是向量长度的一个变化!)
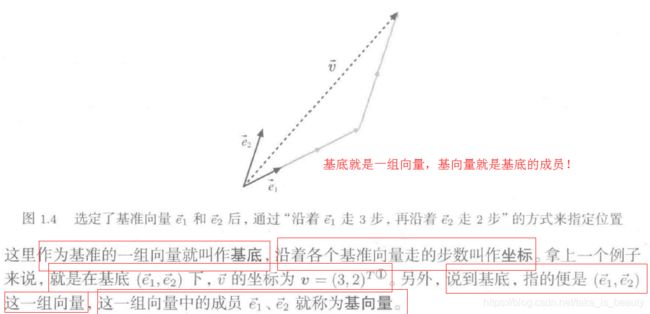
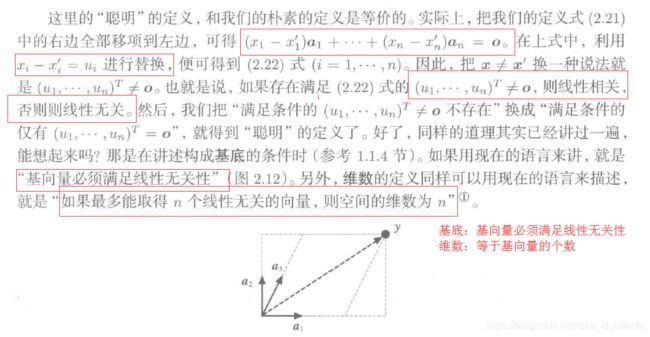
基底和基向量:(一定要清楚:基向量就是在该坐标维度上的单位向量!)
维数:
坐标表示(向量表示):
2.矩阵(矩阵就是映射)(坐标的变换)
矩阵的运算:与标量的运算和向量类似,矩阵乘法也不介绍了(AB = 输出C A的行*B的列)
另一方面也可能计算出来的结果不同!
矩阵就是映射:
矩阵乘一个向量会映射为一个向量;矩阵乘一堆向量(矩阵)就会映射成一堆向量(矩阵)(映射合成!)
单位矩阵:对角元素全为1,其他元素全为0
对角矩阵:对角元素(为实数),其余元素全为0,单位矩阵也是对角矩阵的一种。
逆矩阵:(前提是方阵,且行列式不为零)
还有要证明是Y是X的逆矩阵,只需要证明XY = I即可!(前提:X,Y都是n维方阵)
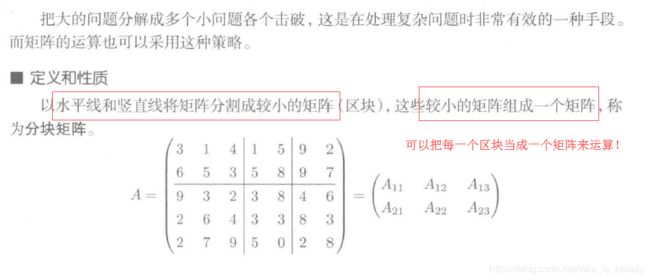
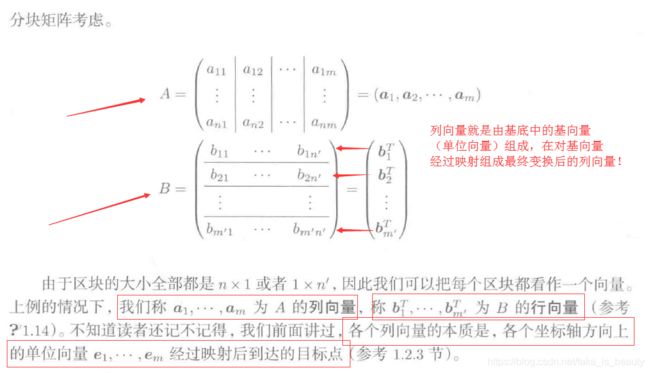
分块矩阵:
一定要清楚:基向量就是在该坐标维度上的单位向量!
坐标变换:矩阵的坐标变换都可以表示为“乘上一个矩阵”的形式!
转置矩阵:
矩阵练习题:
3.行列式(体积扩大率)
行列式就是一个值可以看成是对单位矩阵的变换,行列式对应的方阵里面的基向量围成了一块区域也可以这样解释行列式!
上三角矩阵:对角线下方元素全为零,下三角矩阵定于相反!
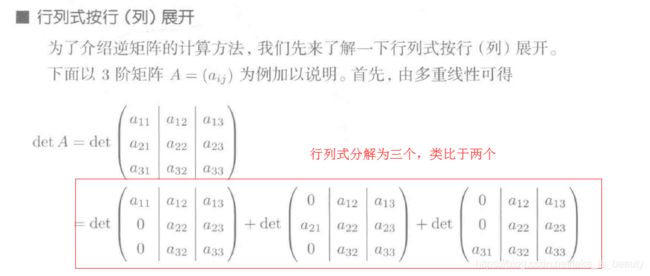
行列式的一些性质:(行列式的多重线性性质)
行列式的计算:
计算逆矩阵公式:
A的行列式值提过去,在同乘一个A的逆即可!!!
第二章:秩、逆矩阵、线性方程组(溯因原理)
1.线性方程组
正则/非正则矩阵:存在逆矩阵的方阵称为正则矩阵/非奇异矩阵;不存在逆矩阵的方阵称为非正则矩阵/奇异矩阵。
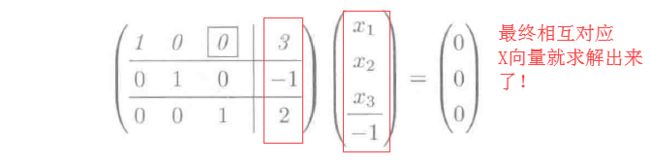
线性方程组的解法:(y = Ax)
使用初等行变换
x = (A | y) -> x = (![]() | x = y*A的逆) !(其实线性解法是系数的变换,而分块矩阵这里也是系数的变换,所以正确!)
| x = y*A的逆) !(其实线性解法是系数的变换,而分块矩阵这里也是系数的变换,所以正确!)
通过线性方程组的解法,来看逆矩阵的解法!
逆矩阵的解法:((A| ![]() ) = (
) = (![]() |A的逆))(只能初等行变换!)
|A的逆))(只能初等行变换!)
初等行变换:(上面计算的本质)
2.线性关系(相关,无关)
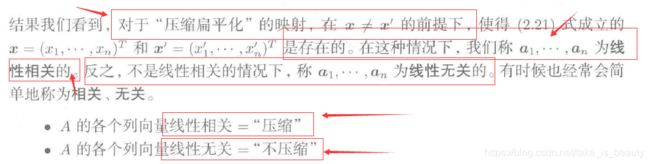
线性相关/无关:
其实相关就是把不同的向量点通过同样的系数进行变换可以映射到相同的y上;而不相关通过同样的系数变换不到相同的y上!
如果基向量线性有关的话,那么就可以用另一个基向量表示,行列式就会被消去就会为零,矩阵消去这一列为0。
矩阵的每列都应该是线性无关的,
3.秩(列的实际个数)
秩的基本概念:
秩的求解也是利用矩阵的初等行变换来进行计算!
一点理解:秩就是所能表达的最大空间维度!
4.逆矩阵
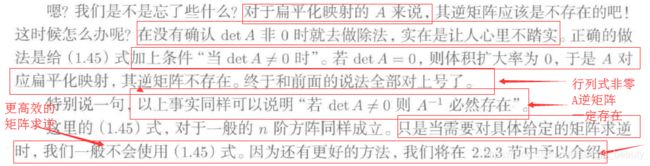
矩阵是扁平化映射(把该维度映射为0,不可逆)则不存在逆矩阵,是非扁平化映射(映射是可逆的)则存在逆矩阵!
可逆矩阵总结:
补充一点:(建立在方阵上)可逆矩阵可以推出矩阵的行列式不为零;然后矩阵的映射为非扁平化映射(因为没有一个维度可以把值映射为零);然后矩阵一定满秩说明每个维度都不为零说明没有一个维度可以被其他维度进行线性组合来表达就说明任意维度之间一定不是线性相关的!
第三章:特征值、对角化
1.对角化
定义:
对角化证明:
验证对角化:
补充一点:(建立在方阵上)可逆矩阵可以推出矩阵的行列式不为零;然后矩阵的映射为非扁平化映射(因为没有一个维度可以把值映射为零);然后矩阵一定满秩说明每个维度都不为零说明没有一个维度可以被其他维度进行线性组合来表达就说明任意维度之间一定不是线性相关的!
2.特征值、特征向量
几何意义:特征向量乘上A之后,除了长度会发生伸缩以外,方向不会发生变化;长度变换倍率便是特征值!
特征值性质:
特征向量的线性无关性:
不相等的特征值对应的的特征向量线性无关。
特征值有重根(前提:特征矩阵可逆,重根个数等价线性无关特征向量个数)。
n个不同的特征值对应n个特征向量组成的矩阵可逆,并且可以将A对角化。
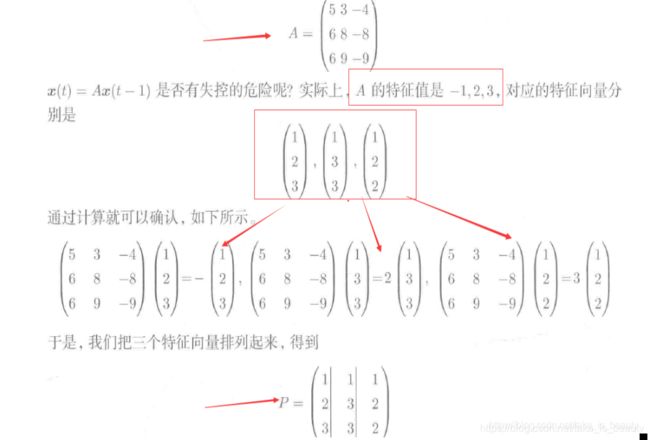
特征值的计算:
迹:A的所有特征值之和。
特征向量的计算:
先求出所有特征值(包括有重根)和特征向量,只要最后特征向量组成的特征矩阵可逆(就可对角化A,等式就成立!)