梯度下降法实现线性回归, 实例---预测波士顿房价

本文先手动实现一个线性回归模型, 然后用sklearn的线性回归模型作对比

import pandas as pd
df = pd.read_csv('house_data.csv')  #数据集可到网上下载,波士顿房价
df.head()

Out[1]:

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222	18.7	396.90	5.33	36.2

In [2]:

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
sns.set(context='notebook')

cols = ['MEDV', 'LSTAT', 'AGE', 'DIS', 'CRIM', 'TAX', 'RM']
sns.pairplot(df[cols], height=2.5)

Out[2]:

In [3]:

from sklearn import datasets
dataset = datasets.load_boston()  #也可以通过sklearn加载数据集

实现线性回归模型

In [4]:

class LinearRegressionByMyself(object):
    def __init__(self, Learning_rate=0.001, epoch=20):
        self.Learning_rate = Learning_rate
        self.epoch = epoch
        
    def fit(self, X, y):
        self.w = np.zeros(1 + X.shape[1])
        self.cost_list = []
        
        for i in range(self.epoch):
            output = self.Regression_input(X)
            #shape重置, 这里需要注意矩阵的运算问题
            output = output.T.reshape(y.shape)
            
            error = (y - output)
            #shape重置
            self.w[1:] += self.Learning_rate * X.T.dot(error).reshape(-1,)
            
            self.w[0] += self.Learning_rate * error.sum()
            cost = (error ** 2).sum() / 2.0
            self.cost_list.append(cost)
        return self
    
    def Regression_input(self, X):
        return np.dot(X, self.w[1:]) + self.w[0]
    
    def predict(self, X):
        return self.Regression_input(X)

模型写完了, 开始准备数据, 并且做数据的预处理 fit_transform

In [5]:

from sklearn.preprocessing import StandardScaler
X = df[['LSTAT']].values   # 这里只去了一维数据
y = df[['MEDV']].values
y = y.reshape(-1,1)

StandardScaler_x = StandardScaler()
StandardScaler_y = StandardScaler()
X_standard = StandardScaler_x.fit_transform(X)
y_standard = StandardScaler_y.fit_transform(y)

实际开始跑模型

In [6]:

model = LinearRegressionByMyself()
model.fit(X_standard, y_standard)

Out[6]:

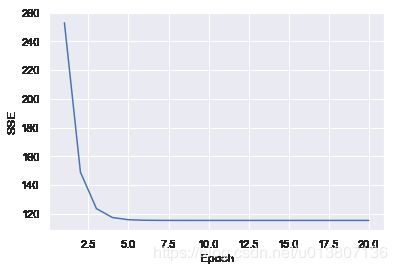
<__main__.LinearRegressionByMyself at 0x1172c0898>

画出模型的损失值随着epoch变化的折线图

可见前三次变化很大, 后面趋于稳定

In [7]:

plt.plot(range(1, model.epoch+1), model.cost_list)
plt.ylabel('SSE')
plt.xlabel('Epoch')

Out[7]:

In [8]:

def Regression_plot(X, y, model):
    plt.scatter(X, y, c='blue')
    plt.plot(X, model.predict(X), color='red')
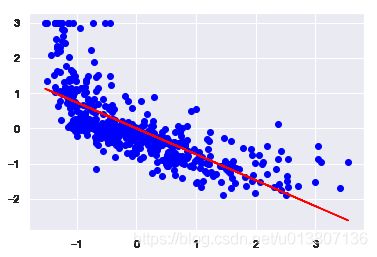
    return None

In [8]:

Regression_plot(X_standard, y_standard, model)

模型已经完成了, 上图看起来效果还不错, 接下来做个实际的预测吧

In [9]:

#这里要注意手动实现的数据, 是做了transform预处理的, 输出实际预测值是还要inverse_transform还原预测值
Rercentage_standard = StandardScaler_x.transform([[23]])
Price_standard = model.predict(Rercentage_standard)
StandardScaler_y.inverse_transform(Price_standard)

Out[9]:

array([ 12.70271311])

使用sklearn构建线性模型

In [10]:

from sklearn.linear_model import LinearRegression
sk_model = LinearRegression()
sk_model.fit(X,y)
print(sk_model.coef_, sk_model.intercept_)

[[-0.95004935]] [ 34.55384088]

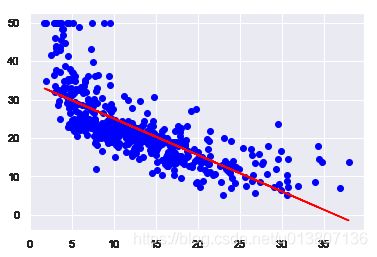
sklearn 只需要3行代码就能实现预测了, 很方便, 还不用数据预处理

In [11]:

Regression_plot(X, y, sk_model)

In [12]:

sk_model.predict(23) #实际预测结果

Out[13]:

array([[ 12.70270574]])