【转】【opencv】仿射变换

仿射变换

目标

在这个教程中你将学习到如何:

1. 使用OpenCV函数 warpAffine 来实现一些简单的重映射.
2. 使用OpenCV函数 getRotationMatrix2D 来获得一个 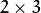 旋转矩阵

原理

什么是仿射变换?

1. 一个任意的仿射变换都能表示为 乘以一个矩阵 (线性变换) 接着再 加上一个向量 (平移).

2. 综上所述, 我们能够用仿射变换来表示:

   1. 旋转 (线性变换)
   2. 平移 (向量加)
   3. 缩放操作 (线性变换)

   你现在可以知道, 事实上, 仿射变换代表的是两幅图之间的 关系 .

3. 我们通常使用 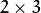 矩阵来表示仿射变换.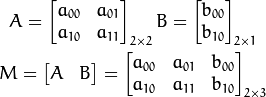

   

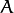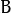   考虑到我们要使用矩阵  和  对二维向量 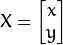 做变换, 所以也能表示为下列形式:

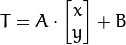    or 

   

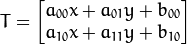
怎样才能求得一个仿射变换?

1. 好问题. 我们在上文有提到过仿射变换基本表示的就是两幅图片之间的 联系 . 关于这种联系的信息大致可从以下两种场景获得:

   1. 我们已知 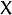 和 T 而且我们知道他们是有联系的. 接下来我们的工作就是求出矩阵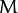 
   2. 我们已知 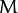 and 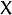. 要想求得 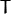. 我们只要应用算式  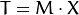即可. 对于这种联系的信息可以用矩阵  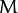清晰的表达 (即给出明确的2×3矩阵) 或者也可以用两幅图片点之间几何关系来表达.

2. 让我们形象地说明一下. 因为矩阵 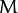 联系着两幅图片, 我们以其表示两图中各三点直接的联系为例. 见下图: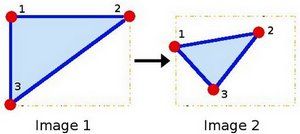

   

   点1, 2 和 3 (在图一中形成一个三角形) 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变. 如果我们能通过这样两组三点求出仿射变换 (你能选择自己喜欢的点), 接下来我们就能把仿射变换应用到图像中所有的点.

例程

1. 这个例程是做什么的?
   • 加载一幅图片
   • 对这幅图片应用仿射变换. 这个变换是从源图像和目标图像的两组三点之间的联系获得的. 这一步我们使用函数 warpAffine 来实现.
   • 仿射变换结束后再对图像应用旋转. 这里的旋转绕图像中点
   • 等待用户退出程序
2. 例程代码在下面给出. 当然你也可以从 这里 下载

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include 
#include 

using namespace cv; using namespace std; /// 全局变量 char* source_window = "Source image"; char* warp_window = "Warp"; char* warp_rotate_window = "Warp + Rotate"; /** @function main */ int main( int argc, char** argv ) { Point2f srcTri[3]; Point2f dstTri[3]; Mat rot_mat( 2, 3, CV_32FC1 ); Mat warp_mat( 2, 3, CV_32FC1 ); Mat src, warp_dst, warp_rotate_dst; /// 加载源图像 src = imread( argv[1], 1 ); /// 设置目标图像的大小和类型与源图像一致 warp_dst = Mat::zeros( src.rows, src.cols, src.type() ); /// 设置源图像和目标图像上的三组点以计算仿射变换 srcTri[0] = Point2f( 0,0 ); srcTri[1] = Point2f( src.cols - 1, 0 ); srcTri[2] = Point2f( 0, src.rows - 1 ); dstTri[0] = Point2f( src.cols*0.0, src.rows*0.33 ); dstTri[1] = Point2f( src.cols*0.85, src.rows*0.25 ); dstTri[2] = Point2f( src.cols*0.15, src.rows*0.7 ); /// 求得仿射变换 warp_mat = getAffineTransform( srcTri, dstTri ); /// 对源图像应用上面求得的仿射变换 warpAffine( src, warp_dst, warp_mat, warp_dst.size() ); /** 对图像扭曲后再旋转 */ /// 计算绕图像中点顺时针旋转50度缩放因子为0.6的旋转矩阵 Point center = Point( warp_dst.cols/2

转载于:https://www.cnblogs.com/sdlypyzq/p/4815654.html