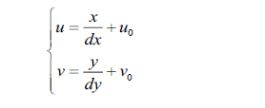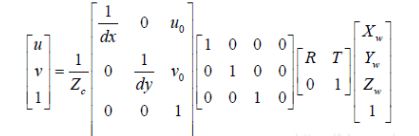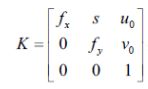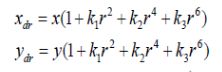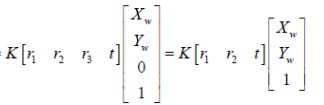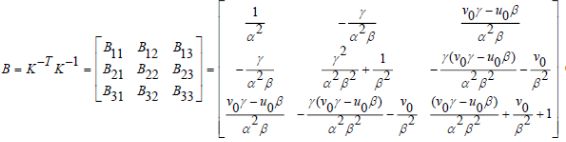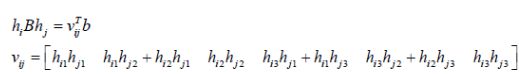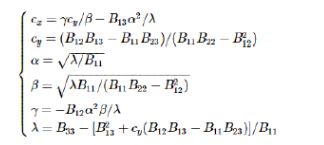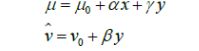相机标定(Camera calibration)Matlab——棋盘格标定原理,流程
计算机视觉----相机标定
相机标定概念:图像测量过程以及计算器视觉中,为确定空间物体某点的三维几何关系位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,模型的参数就是相机的参数。求解参数的过程称为相机标定
开源代码参考
–Intel’s OpenCV library: http://www.intel.com/research/mrl/research/opencv/
–Matlab version by Jean-Yves Bouget: http://www.vision.caltech.edu/bouguetj/calib_doc/index.html
–Zhengyou Zhang’s web site: http://research.microsoft.com/~zhang/Calib/
opencv角点检测、棋盘格检测、亚像素cvFindCornerSubPix()
相机标定(Camera calibration)
OpenCV相机标定和姿态更新
实验步骤:
1.打印一张棋盘格A4纸张(黑白间距已知),并贴在一个平板上
2.针对棋盘格拍摄若干张图片(一般10-20张)
3.在图片中检测特征点(Harris特征)
4.利用解析解估算方法计算出5个内部参数,以及6个外部参数
5.根据极大似然估计策略,设计优化目标并实现参数的refinement
相机成像过程涉及坐标变换
包含世界坐标系(Xw,Yw,Zw),相机坐标(Xc,Yc,Zc),平面坐标(x,y),像素坐标(u,v).
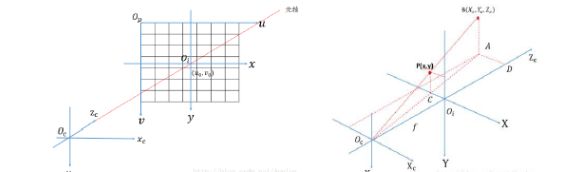
1.1图像坐标系
坐标系中,每个像素坐标都是像素来表示的,但是像素表示不能反映图像中的物理尺寸,所以把像素坐标转换为图像坐标。像素坐标系的原点平移到图像的中心,就定为坐标系的原点,图像坐标系x,y分别与像素坐标系的u,v轴平行,方向相同。相机中感光器件每个像素物理尺寸dx*dy,则图像坐标系中的坐标(x,y)与像素坐标系中的坐标(u,v)之间的关系可以表示为:
改写成其次矩阵形式为:
1.2相机坐标系
相机坐标系以相机的光轴作为z轴,光现在相机的光学系统中心位置就是原点Oc,相机坐标系Xc,Yc分别于图像坐标系X,Y轴平行。相机坐标原点与图像坐标系的原点之间距离OcOf之间的距离f,即焦距。
相机坐标系 立体几何坐标系
由图中的几何关系能够得到:
1.3世界坐标系
世界坐标系图像与真实物体之间的映射关系。也就是真实物体尺寸与图像尺寸的映射关系。相机坐标系到世界坐标系的变换公式为:
其中R=RxRyRz,T=[tx ty tz]T,分别是旋转矩阵和平移矩阵。
相机的内参和外参
外参:摄像机的旋转平移属于外参,用于描述相机在静态场景下相机的运动,或者在相机固定时,运动物体的刚性运动。因此,在图像拼接或者三维重建中,就需要使用外参来求几幅图像之间的相对运动,从而将其注册到同一个坐标系下面来.
内参:下面给出了内参矩阵,需要注意的是,真实的镜头还会有径向和切向畸变,而这些畸变是属于相机的内参的。由前面步骤得到像素坐标系到世界坐标系映射关系:
其中,fx=f/dx,fy=f/dy,f是相机的焦距。RT是外参,矩阵K是内参,包含5个未知数,标定的时候,如果物体距离相机不同位置,那么我们必须在不同位置对相机坐标定。简单理解就是当物体离相机近的时候成像效果大,实际代表尺寸就小。因此每一个位置都要去标定。
图像的畸变以及矫正
2.1径向畸变:
透镜作为中心的原点,往外是透镜的半径方向,光线越靠近中心位置,畸变越小。径向畸变矫正公式:
2.2切向畸变
镜面与成像平面不平行,就产生畸变。类似于透视变换。矫正公式:
作用于真实图像后的矫正模型
畸变就是距离的变化,而距离的变化反应到坐标值上就是加减的关系。
相机的标定原理与方法
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)本实验采用张正友标定法对相机进行标定。在张氏标定中用于标定的棋盘格是三维场景中的一个平面,成像平面的像是另一个平面。知道了这两个对应点的坐标,就可以求解得到两个平面的单应性矩阵H..其中,标定棋盘是特质的,交点坐标是已知的,通过角点的提取算法得到,这样就可以得到棋盘平面和图像平面的单应性矩阵H。通过上面的相机模型,令
H是成像平面和标定棋盘格之间的单应性矩阵,通过对应点解的H后,可以通过上面的等式得到相机内参数K,以及外参旋转矩阵R和平移向量t。假设棋盘格所在的平面为世界坐标Z=0的平面,这样的棋盘格任意一点P的世界坐标为(X,Y,0)。所以第三行r3的数据可以被省略。↓
由于每个单应性方程能提供两个方程,内参数矩阵包含5个方程,要求解至少需要3个单应性矩阵,使用至少三幅棋盘格对图片进行标定,改变相机与标定板之间的相对位置来得到三个不同的图片,通过图像得到关于内参数的两个等式,令
对称B是一个对称矩阵,未知量只有6个,将6个未知量写成向量的形式
令hi为单应性矩阵的第i个行向量,则有:
故:
结合上面两式重写矩阵可以推导出:
上面是取得约束的约束等式,假如n幅图像,则V是2n×6“的矩阵。Vb=0最后,使用SVD求解最小二乘,得到相机的各个内参数
以及外参数。
注意: 当观测平面 n ≥ 3 时,可以得到b的唯一解
当 n = 2时, 一般可令畸变参数γ = 0
当 n = 1时, 仅能估算出α 与 β, 此时一般可假定像主点坐标 u0 与 v0 为0
实验结果?:
两个照片:
发现出现了虚数,没有得到唯一解
用三个:
四个:
五个:(得到的结果越来越精确)
消除径向畸变
张氏标定法只关注了较大的径向畸变,设(u,v)是理想无畸变的像素坐标,![]()
是畸变后的像素坐标,使用下面式子表示径向畸变:
K1,K2分别表示径向畸变的系数,径向畸变的中心和相机中心是在相同的位置。
假设y=0,则有:
和上面类似,利用最大似然估计取得最优解,利用LM的方法估计使得下面式子是最小值的参数值
得到畸变参数之后,现将图像进行去畸变处理。然后用去畸变后图像坐标估计相机的内参数
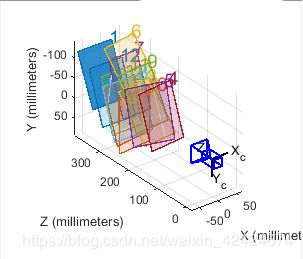
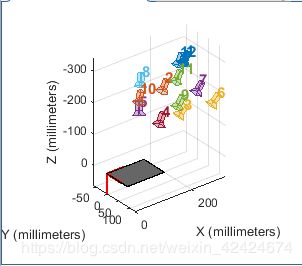
数据采集,(12张图) 确定角点范围
角点提取 :
参数解算:
输入cameraParams.IntrinsicMatrix得到相机内参矩阵 cameraParams.RadialDistortion径向畸变