张正友标定法——相机参数的标定

张正友标定法也称棋盘格标定法，是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。该方法介于传统的标定方法和自标定方法之间，使用简单实用性强，有以下优点：

• 不需要额外的器材，一张打印的棋盘格即可。
• 标定简单，相机和标定板可以任意放置。
• 角点明显，标定的精度高。

1.1 相机的内参矩阵

设P=(X,Y,Z)为场景中的一点，在针孔相机模型中，其要经过以下几个变换，最终变为二维图像上的像点p=(μ,ν):

1. 将P从世界坐标系通过刚体变换(旋转和平移)变换到相机坐标系，这个变换过程使用的是相机间的相对位置，也就是相机的外参数。
2. 从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)。
3. 将像点p从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν)。

相机将场景中的三维点变换为图像中的二维点，也就是各个坐标系变换的组合，可将上面的变换过程整理为矩阵相乘的形式：

将矩阵K称为相机的内参数,

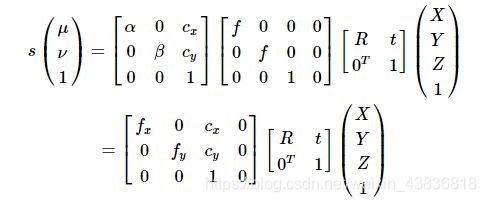
其中，α,β表示图像上单位距离上像素的个数，则f_x=αf,f_y=βf将相机的焦距f变换为在x,y方向上像素度量表示。
另外，为了不失一般性，可以在相机的内参矩阵上添加一个畸变参数γ，该参数用来表示像素坐标系两个坐标轴的畸变大小。则内参矩阵K变为

1.2 张正友标定法

该方法将位于棋盘格上的点的Z坐标都设为0，即

再利用homographic（共线方程）进行单应性变换，得到棋盘平面Π和图像平面π的单应矩阵H。再根据上式可得出将棋盘格所在的平面映射到相机的成像平面的方程。其中p为棋盘格所成像的像点坐标，P棋盘格角点在世界坐标系的坐标。
将上面两个等式进行整合，则可以得到单应矩阵H和相机矩阵（包含内参和外参）的相等：

这样就可以使用棋盘平面和成像平面间的单应矩阵来约束相机的内参和外参。单应矩阵H可以通过棋盘平和成像平面上对应的点计算出来。

1.3 OpenCV中的张正友相机标定

OpenCV中提供了对张正友标定算法的实现，其使用步骤如下：

1. 制作棋盘格标定板——可以将其打印下来固定到一张平板上就是标定使用的标定板。使用同一相机从不同的位置，不同的角度，不同的姿态，拍摄标定板的多张照片（一般不少于3张，以10-20张为宜）。
2. 提取标定板的内角点的世界坐标，这里需要注意标定板的大小是标定板在水平和竖直方向上内焦点的个数。内焦点指的是，标定板上不挨着边的角点。比如棋盘格的大小是4*6，其在水平方向有3个内焦点；竖直方向有5个内焦点。
3. 提取标定板的角点的图像坐标。
4. 对已经取得了角点的世界坐标以及对应的像素坐标进行标定。

1.3.1 代码及运行结果

本次实验用了15*12为大小的棋盘格。并用华为P20pro拍摄了十张不同位置、不同角度的图像。

下面是实现代码：

#-*- coding:utf-8 -*-

import cv2
import glob
import numpy as np
'''
cbraw和cbcol是棋盘的角点矩阵大小，这里如果角点维数超出的话，标定的时候会报错。
'''
cbraw = 11
cbcol = 14
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((cbraw*cbcol,3), np.float32) 
'''
设定世界坐标下点的坐标值，因为用的是棋盘可以直接按网格取；
假定棋盘正好在x-y平面上，这样z值直接取0，简化初始化步骤。
mgrid把列向量[0:cbraw]复制了cbcol列，把行向量[0:cbcol]复制了cbraw行。
转置reshape后，每行都是11*14网格中的某个点的坐标。
'''
objp[:,:2] = np.mgrid[0:cbraw,0:cbcol].T.reshape(-1,2)

objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
#glob是个文件名管理工具
images = glob.glob("*.jpg")
for fname in images:
#对每张图片，识别出角点，记录世界物体坐标和图像坐标
    img = cv2.imread(fname) #source image
    #我用的图片太大，缩小了一半
    img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转灰度
    #cv2.imshow('img',gray)
    #cv2.waitKey(1000)
    #寻找角点，存入corners，ret是找到角点的flag
    ret, corners = cv2.findChessboardCorners(gray,(11,14),None)
    #criteria:角点精准化迭代过程的终止条件
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    #执行亚像素级角点检测
    corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

    objpoints.append(objp)
    imgpoints.append(corners2)
    #在棋盘上绘制角点,只是可视化工具
    img = cv2.drawChessboardCorners(gray,(11,14),corners2,ret)
    cv2.imshow('img',img)
    #cv2.waitKey(1000)
'''
传入所有图片各自角点的三维、二维坐标，相机标定。
每张图片都有自己的旋转和平移矩阵，但是相机内参和畸变系数只有一组。
mtx，相机内参；dist，畸变系数；revcs，旋转矩阵；tvecs，平移矩阵。
'''
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)

#打印我们要求的两个矩阵参数
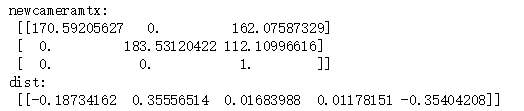
print ("newcameramtx:\n",newcameramtx)
print ("dist:\n",dist)

运行结果：

由结果可看出，焦距f_x=170.59,及f_y=183.53（约等于）。