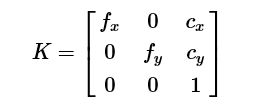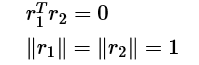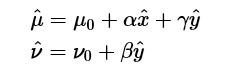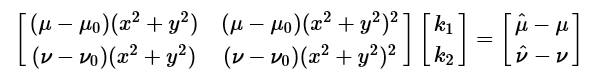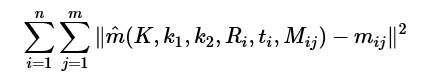计算机视觉学习（六）：标定手机相机参数

本次实验使用的是张正友的相机标定方法，该方法介于传统的标定方法和自标定方法之间，使用简单实用性强，有以下优点：

•    不需要额外的器材，一张打印的棋盘格即可
•    标定简单，相机和标定板可以任意放置
•    标定的精度高

下面是张正友相机标定法的详解

---

相机的内参数

设P=(X,Y,Z)P=(X,Y,Z)为场景中的一点，在针孔相机模型中，其要经过以下几个变换，最终变为二维图像上的像点p=(μ,ν)p=(μ,ν):

1. 将PP从世界坐标系通过刚体变换(旋转和平移)变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
2. 从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)p=(x,y)。
3. 将像点pp从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν)p=(μ,ν)。

相机将场景中的三维点变换为图像中的二维点，也就是各个坐标系变换的组合，可将上面的变换过程整理为矩阵相乘的形式：

将矩阵KK称为相机的内参数,

其中，α,βα,β表示图像上单位距离上像素的个数，则fx=αf,fy=βffx=αf,fy=βf将相机的焦距ff变换为在x,y方向上像素度量表示。

另外，为了不失一般性，可以在相机的内参矩阵上添加一个扭曲参数γγ，该参数用来表示像素坐标系两个坐标轴的扭曲。则内参数KK变为

张氏标定法

在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面ΠΠ，其在成像平面的像是另一个平面ππ，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵HH。其中，标定的棋盘格是特制的，其角点的坐标是已知的；图像中的角点，可以通过角点提取算法得到，这样就可以得到棋盘平面ΠΠ和图像平面ππ的单应矩阵HH。
通过上面的相机模型有：

其中pp是像点坐标，PP是标定的棋盘坐标。 这样就可以得到下面的等式：

HH表示的是成像平面和标定棋盘平面之间的单应矩阵。通过对应的点对解得HH后，则可以通过上面的等式得到相机的内参数KK，以及外参旋转矩阵RR和平移向量tt。

棋盘平面和成像平面间的单应

将一个平面映射到另一个平面，将棋盘格所在的平面映射到相机的成像平面，则有

pp为棋盘格所成像的像点坐标，PP棋盘格角点在世界坐标系的坐标。

设棋盘格所在的平面为世界坐标系中Z=0Z=0的平面，这样棋盘格的任一角点PP的世界坐标为(X,Y,0)(X,Y,0)，根据小孔相机模型：

根据平面间的单应性，有

将上面两个等式进行整合，则可以得到单应矩阵HH和相机矩阵（包含内参和外参）的相等，如下：

这样就可以使用棋盘平面和成像平面间的单应矩阵来约束相机的内参和外参。单应矩阵HH可以通过棋盘平和成像平面上对应的点计算出来。

内参的约束条件

通过平面间的单应，可以得到如下的等式

将旋转矩阵RR的各个列向量和平移向量tt使用HH的列向量表示，

又由于，RR是旋转矩阵，则其是正交矩阵，也就是其任意两个列向量的内积为0，列向量的模为1。故有：

则对于一幅棋盘标定版的图像（一个单应矩阵）可以获得两个对内参数的约束等式：

求解内参数

通过一幅标定板的图像可以的得到关于内参数的两个等式，令

注意，矩阵BB是一个对称矩阵，其未知量只有6个，将6个未知量写为向量的形式

令hihi为单应矩阵HH的第ii个行向量，则有

故

从而可以得到相机的各个内参数：

最大似然估计

上面使用最小二乘法得到估计得到的解，并没有物理上的实际意义，。为了进一步增加标定结果的可靠性，可以使用最大似然估计(Maximum likelihood estimation)来优化上面估计得到的结果。

假设同一相机从nn个不同的角度的得到了nn幅标定板的图像，每幅图像上有mm个像点。MijMij表示第ii幅图像上第jj个像点对应的标定板上的三维点，则

m^(K,Ri,ti,Mij)m^(K,Ri,ti,Mij)表示MijMij的像点。其中，Ri,tiRi,ti表示第ii幅图像对应相机的旋转矩阵和平移向量，KK是相机的内参数。则像点mijmij的概率密度函数是

构造似然函数

为了能够让LL取得最大值，需要最小化下面的值

这是一个非线性优化问题，可以使用Levenberg-Marquardt的方法，利用上面得到的解作为初始值，迭代得到最优解。

消除径向畸变

为取得好的成像效果，通常要在相机的镜头前添加透镜。在相机成像的过程中，透镜会对光线的传播产生影响，从而影响相像效果，产生畸变：

• 透镜自身的形状对才光线的传播产生影响，形成的畸变称为径向畸变。在小孔模型中，一条指向在成像平面上的像仍然是直线。但是在实际拍摄的过程中，由于透镜的存在，往往将一条直线投影成了曲线，越靠近图像的边缘，这种现象越明显。透镜往往是中心对称的，使得这种不规则的畸变通常是径向对称的。主要有两大类：桶形畸变和枕形畸变。如下图

• 由于在相机组装的过程中，透镜不能和成像平面严格平行，会引入切向畸变。

张氏标定法中只关注了影响较大的径向畸变。
设，(μ,ν)(μ,ν)是理想的无畸变的像素坐标；(μ^,ν^)(μ^,ν^)是畸变后的像素坐标；(μ0,ν0)(μ0,ν0)是相机的主点；(x,y)(x,y)和(x^,y^)(x^,y^)理想的无畸变的归一化的图像坐标和畸变后的归一化图像坐标，使用下面的式子表示径向畸变：

k1,k2k1,k2表示径向畸变的系数。径向畸变的中心和相机的主心是在相同的位置，

假设γ=0γ=0，则有：

将上面的式子改写为矩阵的形式

上面的等式是从一幅图像上的一个点取得，设有nn幅图像，每幅图像上有mm个点，则将得到的所有等式组合起来，可以得到2mn2mn个等式，将其记着矩阵形式

则可得

和上面类似利用最大似然估计取得最优解，使用LM的方法估计使得下面式子是最小值的参数值

得到畸变参数k1,k2k1,k2后，可以先将图像进行去畸变处理，然后用去畸变后的图像坐标估计相机的内参数。

参考：https://www.cnblogs.com/wangguchangqing/p/8335131.html

---

本次实验运行的代码如下：

#!usr/bin/env/ python
# _*_ coding:utf-8 _*_

import cv2 as cv
import numpy as np
import os
from step.homography import get_homography
from step.intrinsics import get_intrinsics_param
from step.extrinsics import get_extrinsics_param
from step.distortion import get_distortion
from step.refine_all import refinall_all_param


def calibrate():
    #求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    #求内参
    intrinsics_param = get_intrinsics_param(H)

    #求对应每幅图外参
    extrinsics_param = get_extrinsics_param(H, intrinsics_param)

    #畸变矫正
    k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)

    #微调所有参数
    [new_intrinsics_param, new_k, new_extrinsics_param]  = refinall_all_param(intrinsics_param,
                                                            k, extrinsics_param, real_points, pic_points)

    print("intrinsics_parm:\t", new_intrinsics_param)
    print("distortionk:\t", new_k)
    print("extrinsics_parm:\t", new_extrinsics_param)


if __name__ == "__main__":
    file_dir = r'..\pic\data'
    # 标定所用图像
    pic_name = os.listdir(file_dir)

    # 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标
    cross_corners = [9, 5] #棋盘方块交界点排列
    real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)
    real_coor[:, :2] = np.mgrid[0:9, 0:5].T.reshape(-1, 2)

    real_points = []
    real_points_x_y = []
    pic_points = []

    for pic in pic_name:
        pic_path = os.path.join(file_dir, pic)
        pic_data = cv.imread(pic_path)

        # 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)

        if succ:
            # 添加每幅图的对应3D-2D坐标
            pic_coor = pic_coor.reshape(-1, 2)
            pic_points.append(pic_coor)

            real_points.append(real_coor)
            real_points_x_y.append(real_coor[:, :2])
    calibrate()

其中要对运行的图片进行调整大小和修改灰度图，使用到了如下代码：

import cv2
#循环灰度图片并保存
def grayImg():
    for x in range(1,13):
        #读取图片
        img = cv2.imread("D:\work\shijue\Camera-Calibration-of-Zhang-s-method-master\pic\{}.jpg".format(str(x)))
        GrayImage=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
        GrayImage=cv2.resize(GrayImage,(1000,1333))
        #保存灰度后的新图片
        cv2.imwrite("D:\work\shijue\Camera-Calibration-of-Zhang-s-method-master\pic\data\{}.jpg".format(str(x)),GrayImage)
grayImg()

---

本次实验图片素材使用步骤：

1. 制作标定板，我制作的是一个10*6，每个方格2.5cm的标定板
2. 将其打印出来放到平面上，使用同一部手机从不同角度，不同位置，不同姿态，拍摄标定板的多张照片（我拍了13张，一般在10-20张为宜）
3. 经过处理后的长这样

---

本次实验运行的结果如下：

使用的手机型号为iphone6s plus

使用的手机型号为iphone6s plus

 

相机标定的目的：获取摄像机的内参和外参矩阵（同时也会得到每一幅标定图像的选择和平移矩阵），内参和外参系数可以对之后相机拍摄的图像就进行矫正，得到畸变相对很小的图像。
相机标定的输入：标定图像上所有内角点的图像坐标，标定板图像上所有内角点的空间三维坐标（一般情况下假定图像位于Z=0平面上）。
相机标定的输出：摄像机的内参、外参系数。
 

从上面结果可以看到

   相机的内参微调后为

      array([[2.21747928e+03, 1.32935566e+01, 1.08477421e+03],
       [0.00000000e+00, 2.29788647e+03, 9.10011052e+02],
       [0.00000000e+00, 0.00000000e+00, 1.00000000e+00]]))

   相机的畸变校正微调后为

      array([-0.00088124,  0.00080136]

   对应每幅图外参微调后为

      array([[[ 8.28548254e-01, -1.20020899e-01, -5.46902893e-01,

         -9.95214625e+00],
        [-1.57220298e-01,  8.87590264e-01, -4.32972633e-01,
         -8.02643293e+00],
        [ 5.37391447e-01,  4.44722955e-01,  7.16541642e-01,
          2.91406294e+01]],

       [[ 7.71388660e-01, -6.14482396e-01, -1.65441591e-01,
         -1.13408073e+01],
        [ 6.28905658e-01,  7.75821077e-01,  5.07871035e-02,
         -5.30156339e+00],
        [ 9.71452920e-02, -1.43223748e-01,  9.84911037e-01,
          3.54183387e+01]],

       [[ 7.43985835e-01,  6.62950573e-01,  8.35560621e-02,
         -1.19391022e+01],
        [-6.57052881e-01,  7.03096068e-01,  2.71914381e-01,
         -1.40906717e+00],
        [ 1.21517856e-01, -2.57201199e-01,  9.58687099e-01,
          3.44849999e+01]],

       [[ 1.01451393e-01,  9.94789174e-01,  1.01051226e-02,
         -8.19124078e+00],
        [-9.94840226e-01,  1.01438633e-01,  1.76870295e-03,
          1.96514742e+00],
        [ 7.34436723e-04, -1.02324198e-02,  9.99947378e-01,
          2.11614442e+01]],

       [[ 1.55021703e-01,  9.42505965e-01, -2.96058738e-01,
         -9.40874116e+00],
        [-8.96294847e-01,  2.60216644e-01,  3.59086125e-01,
          6.38443602e-01],
        [ 4.15480226e-01,  2.09689779e-01,  8.85102468e-01,
          3.14034908e+01]],

       [[ 9.94283116e-01, -3.52572501e-02,  1.00786961e-01,
         -1.21930077e+01],
        [ 6.28668540e-02,  9.56262422e-01, -2.85674535e-01,
         -6.19738223e+00],
        [-8.63066847e-02,  2.90377526e-01,  9.53012093e-01,
          3.22029455e+01]],

       [[ 2.75578518e-01, -5.77981478e-01, -7.68110599e-01,
         -7.77846438e+00],
        [ 5.74111976e-01,  7.39849638e-01, -3.50739151e-01,
         -1.06402407e+01],
        [ 7.71007081e-01, -3.44325318e-01,  5.35712755e-01,
          3.59370849e+01]],

       [[ 8.82756375e-01,  2.45753677e-01, -4.00432656e-01,
         -1.12285826e+01],
        [-1.54941747e-01,  9.56885319e-01,  2.45689928e-01,
         -3.17205656e+00],
        [ 4.43547333e-01, -1.54840615e-01,  8.82774120e-01,
          3.00242298e+01]],

       [[ 5.18319478e-01, -7.86817098e-01, -3.35057866e-01,
         -9.86088625e+00],
        [ 8.07496753e-01,  5.79295715e-01, -1.11200128e-01,
         -7.73380264e+00],
        [ 2.81591748e-01, -2.12920947e-01,  9.35612504e-01,
          3.58593526e+01]],

       [[ 7.65808489e-01, -5.59162186e-01, -3.17608263e-01,
         -1.15359440e+01],
        [ 5.50212460e-01,  8.25390798e-01, -1.26476401e-01,
         -6.13991365e+00],
        [ 3.32871758e-01, -7.78953220e-02,  9.39749281e-01,
          3.68239032e+01]],

       [[ 4.86661352e-01,  8.73425928e-01, -1.69669296e-02,
         -1.12922015e+01],
        [-7.96107070e-01,  4.35416277e-01, -4.20269197e-01,
         -1.69800212e+00],
        [-3.59686336e-01,  2.18036269e-01,  9.07240831e-01,
          3.35822044e+01]],

       [[ 6.10655913e-01, -7.46819761e-01,  2.63362108e-01,
         -9.81220894e+00],
        [ 7.83181461e-01,  6.18761574e-01, -6.13262822e-02,
         -5.30246667e+00],
        [-1.17158673e-01,  2.43709577e-01,  9.62745806e-01,
          3.29294689e+01]]])

   总误差为：3.0132405503782076