Dijkstra算法的原理与实现

       主流的最短路径算法主要有Dijkstra和Floyd算法。相比于Floyd算法，笔者认为Dijkstra算法在理解上更具难度性。因此查阅并参考了诸多博客，书籍资料，浅谈对Dijkstra算法的理解。

1. Dijkstra算法核心思想

        Dijkstra算法是基于贪心算法思想的。所谓贪心算法即始终保持当前迭代解为当前最优解。意思就是在已知的条件下或是当前拥有的全部条件下保证最优解，若在此后的迭代中由于加入了新的条件使得产生了更优解则替代此前的最优解。通过不断的迭代不断保证每次迭代的结果都是当前最优解，那么当迭代到最后一轮时得到的就会是全局最优解。

        由于下一轮迭代会参考上一轮的最优解，因此每一轮的迭代的工作量基本一致，降低了整体工作的复杂性。

       在最短路径的问题中，局部最优解即当前的最短路径或者说是在当前的已知条件下起点到其余各点的最短距离。

       到这里读者可能要问了，当前的已知条件指的是啥？难道所有的条件不是问题都已给出的吗？

2.  一个奇妙的构想

       理解Dijkstra算法我们先做一个构想：首先假设问题所给出的所有的顶点和路径都不存在。接下来进行n轮迭代（n为顶点数），每轮迭代加入一个顶点，第一轮加入起点。没加入一个顶点就将与其相连的边加入，但边的另一边的顶点不立即加入。这样就产生了前面我所说的当前的已知条件，即已加入的顶点和边。那么接下来只需要保证起点到其余各顶点距离当前最短即可。

3.  简单的替代原理

       前面我们说了如果下一轮迭代的最短路径比前一轮更短，则需要进行替代，以本轮的路径作为当前最短路径。那么究竟是基于什么进行替代的呢？

           

      如上图，从1到3有两条路径，分别是1-->3，1-->2-->3。若我们上一轮迭代的结果为1-->3为最短路径，而本轮结果为1-->2-->3更短，则用1-->2-->3替代1-->3。实际上无论是Dijkstra还是Floyd算法，在进行路径更新时都是由于类似上图这种情况，即到达某一顶点产生了新的路径，而这一路径更短。

      下面我们来以一个例子具体说明Dijkstra迭代过程。

4. Dijkstra算法核心原理

      在2所说的构想的基础上，在初始为空的顶点集合中每轮加入一个未访问过的顶点（第一轮加入起点），并将该顶点相邻的边作为我们新一轮迭代的条件。若新加入的相邻边能到达的顶点距离比上一轮迭代起点到该点的距离更短则更新路径，并将该点加入集合（不更新也加入）。这样就保证了在本轮结束后起点到该新加入的点的距离当前最短。

5. 一个简单的例子

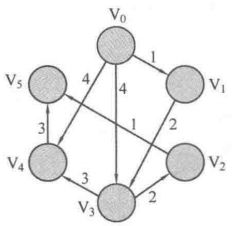
       如上图，以V0为起点，图中已标出各顶点及路径长度，下面我们来迭代计算V0到各顶点的最短距离。

      （1）第一轮：将V0以及V0相邻的V0-->V1，V0-->V3，V0-->V4加入，并更新V0-->V1距离为1，V0-->V3距离为4，V0-->V4距离为4

      （2）第二轮：在（1）三条路径中V0-->V1最短，将V1及V1-->V3加入

      （3）第三轮：由于V1-->V3的加入，计算V0-->V1-->V3 < V0-->V3，因此更新V0到V3路径为V0-->V1-->V3。加入V3及V3-->V4，V3-->V2

      （4）第四轮：V0-->V1-->V3-->V2为唯一路径，更新V0到V2的距离为V0-->V1-->V3-->V2，加入V2及V2-->V5

      （5）第五轮：V0-->V3-->V4 < V0-->V4，不更新，加入V4及V4-->V5

      （6）第六轮：V0-->V4-->V5 < V0-->V1-->V3-->V2-->V5，更新V0到V5的距离为V0-->V1-->V3-->V2-->V5

       迭代完成，到各顶点的最短距离也都完成。下面我们来谈谈代码实现

6. 代码实现

      对于图的存储主要有邻接矩阵和邻接表两种方式，这里我们只谈邻接矩阵，邻接表同理。

      我们需要创建一个邻接矩阵以存储图；一个最短路径数组存储起点到各点的最短路径，算法中不停迭代更新的就是这个数组，初始均为无穷大；一个辅助数组表示各点是否被访问过，因为从上面的例子中可以看出每轮迭代访问的必须是此前未访问过的顶点，初始均为false。至此，所有准备工作完成。

int G[MAXV][MAXV];     //邻接矩阵
int d[MAXV];      //最短距离
bool vis[MAXV] = {false};      //顶点是否访问辅助矩阵

void Dijkstra(int s){
    fill(d, d+MAXV, INF);
    d[s] = 0;
    for(int i=0; i         int u = -1;    //使d[u]最小
        int MIN = INF;      //MIN存放最小d[u]
        for(int j=0; j             if(vis[j] == false && d[j] < MIN){
                u = j;
                MIN = d[j];
            }
        }
        if(u == -1) return;      //剩下的顶点和起点s不连通
        vis[u] = true;
        for(int v=0; v             if(vis[v] == false && G[u][v] != INF && d[u] + G[u][v] < d[v]){
                 d[v] = d[u] + G[u][v]; 
            }
        }
    }
}

      以上代码仅供参考，欢迎指正批评。