基于矢量量化的图像压缩

 

1. 引言

矢量量化是19世纪70年代后期发展起来的一种数据压缩技术，其基本思想是将若干个标量数据组构成一个矢量，然后在矢量空间给以整体量化，从而压缩了数据而不损失多少信息。矢量量化编码也是在图像、语音信号编码技术中研究得较多的新型量化编码方法，它的出现并不仅仅是作为量化器设计而提出的，更多的是将它作为压缩编码方法来研究的。在传统的预测和变换编码中，首先将信号经某种映射变换变成一个数的序列，然后对其一个一个地进行标量量化编码。而在矢量量化编码中，则是把输入数据几个一组地分成许多组，成组地量化编码，即将这些数看成一个k维矢量，然后以矢量为单位逐个矢量进行量化。矢量量化是一种限失真编码，其原理仍可用信息论中的率失真函数理论来分析。而率失真理论指出，即使对无记忆信源，矢量量化编码也总是优于标量量化。

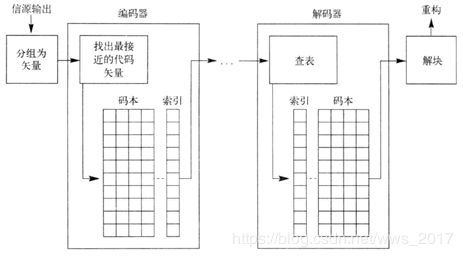
在矢量量化中，我们将信源输出进行分组，变为块或者矢量。例如，可以将L个连续语音样本看成一个L维矢量的分量。或者，可以取得一个由某图像中L个像素组成的块，将每个像素值看做一个L维矢量的分量。这种信源输出矢量构成了矢量量化器的输入。在矢量量化器的编码器和解码器处，都有一个L维矢量组成的集合，称为矢量量化器的码本。这一码本中的矢量称为代码矢量，选择用来表示由信源输出生成的矢量。每个代码矢量都被指定一个二进制索引。在编码器端，将输入矢量与每个代码矢量进行对比，找出与输入矢量最接近的代码矢量。这一代码矢量的元素就是信源输出的量化值。为了告诉解码器，哪个代码矢量与输入矢量最接近，我们传送或存储该代码矢量的索引。因为解码器拥有完全相同的码本，所以它能够根据二进制索引来提取该代码矢量，其过程结构图如图1所示。

图1 矢量量化过程

     2. 矢量量化原理

矢量量化（VQ）实际上就是一种逼近的形式，它的思想和“四舍五入”有异曲同工之妙，都是用一个和一个数最接近的整数来近似表示这个数。VQ问题可以这样描述：给定一个已知统计属性的矢量源（也就是训练样本集，每一个样本是一个矢量）和一个失真测度。还给定了码矢的数量（也就是我们要把这个矢量空间划分为多少部分，或者说量化为多少种值），然后寻找一个具有最小平均失真度（数据压缩，肯定是失真越小越好）的码书和空间的划分。

假定我们有一个有M个矢量源（训练样本）的训练序列（训练集）：

T=x1,x2,…,xM 

这个训练序列可以通过一些大数据库得到。如果这个矢量源是语音的话，那么我们就可以对一些电话录音裁剪得到。我们假设M足够大（训练样本足够多），这样才可以保证这个训练序列包含了矢量源的所有统计特性。我们假设源矢量是k维的：

xm=xm,1,xm,2,…,xm,k   m=1,2,…,M 

假设码本矢量的数目是N（也就是我们要把这个矢量空间划分为N个部分，或者说量化为N种值），码书（所有码矢的集合）表示为：

C=c1,c2,…,cN 

每一个码矢是个k维向量：

Cn=cn,1,cn,2,…,cn.k  n=1,2,…,N 

与码本矢量Cn 对应的编码区域表示为Sn ，然后将空间的划分表示为：

P=S1,S2,…,SN 

如果源矢量xm 在Sn 内，那么它的近似(用Q(xm) 表示)就是cn :

Qxm=cn   如果xm属于Sn 

假设我们采用均分误差失真度量，那么平均失真度表示如下：

Dave=1MKm=1Mxm-Qxm2 

这里e2 为欧式距离。那么设计问题就可以简单的描述为：给定T（训练集）和N（码本矢量数目），找到能使得平均失真度最小的码书和空间划分。

3. LBG算法的实现

在矢量量化的过程中最常用的算法就是LBG算法，它是一种迭代的算法，使得失真度不断地趋向于它的局部最小值。这个算法需要一个初始的码书，初始化码书的方法有多种，有随机法、分割法（扰动）、成对最近邻（PNN）算法和Hibert法，可以根据实际应用场景选择合适的初始码本的技术。这里介绍一个初始码本可以通过分割方法得到的思想，这个方法主要是把一个初始码矢设置为所有训练样本的平均值。然后把这个码矢分裂成两个（分裂的方式见下面的LBG算法的第3步的公式，只要是乘以一个扰乱系数）。把这两个码矢作为初始的码书，然后迭代算法就在这个初始的码书上面跑。它每一次都将每个码矢分裂为2个，重复这个过程，直到获得要求的码矢个数。1个分裂为2个，2个分裂为4个，4个分裂为8个等，但是如果想要生成7个矢量的码书需要在分裂成四个时随机选择其中的三个作为下一次的分裂对象即可实现。

从实用角度来看，我们更关系的是在有训练集可用时采用的算法。在这种情况下，该算法非常类似于均值算法。

Step1：首先给出重构值的一个初始集合yi(1)i=1M ，一个训练矢量集合xnn=1N 。设定k=1 ,

D(0)=0 。选择阈值ε 。

Step2：量化区域Vi(k)i=1M 给出如下：

Vi(k)=xn:dxn,yixn,yi ∀j≠i  j=1,2,…,M 

假定所有量化区域都不是空的。（后面将会讨论Vi(k) 对于某个i和k为空的情景）

Step3：计算训练矢量和典型重构值之间的平均失真度D(k) 

D(k)=1Ni=1Mxn∈V(k)xn-yi2 

Step4：如果D(k)-D(k-1)D(k)<ε ，则停止，否则，继续。

Step5：k=k+1，计算新的重构值yi(k)i=1M ，它是每个量化区域Vi(k-1) 的元素平均值。转至第Step2中。

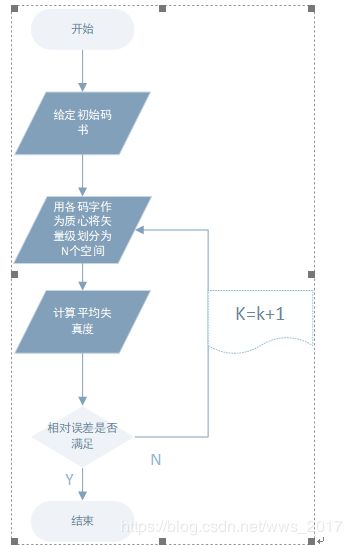
其流程图如图2所示。

图2 LBG算法基本流程图

本次实验是对真实一副图像进行矢量量化的处理，分别采用在不同的码书大小的条件下观察比较相应的结果，采用的码本大小分为：16、64、256和1024，仿照书本上的参数进行设定。

4. 图片压缩实验及结果分析

选取网上一个彩色图像做灰度化，然后对灰度化后的图像进行处理，其中码字大小都选择16，码书个数分别为16、64、256和1024进行实验。其彩色图像和灰度化后的图像如图所示。

图3 原始图像的处理

使用大小为16、64、256和1024的码本得到的量化结果如图所示。

    

图4 量化后的结果图

从课本和实际操作的过程中，我们知道随着码本的大小的增加，我们对图像的压缩比在不断缩小，所以图像的重构也越来越接近原始灰度化的图像，从上图的实例中也可以证明这一点。观察这些重构后的图像，可以看出当使用大小为1024的码本进行重构时，其结果与原图像最为相近，相比较而言，如果重构时选择使用的码本中包括16个重构矢量时，则可以在所得到的图像中看到大量伪像。

但是我想知道，是不是随着码书的不断增大，它的重构图像越来越接近原始图像那，但是结果却不是这样的，我又做了码书大小为512和2048的重构，如图所示。发现其实当码书再次增大后，其重构图像的变化不是很大。

  

我们根据实验发现，随着码书的增大，其重构结果的改变不是很大，那么码字对于重构图像是否有影响那，所以我选择了当码书为1024时，码字分别为1、4、8和10的实验进行测试，其结果如图所示。

  

  

图5 码字不同的重构效果图

结合上述图片可以明显的看出，码字对图像的重构影响挺明显的，当码字变小时，图片的轮廓更加清晰，而码字变大时，图像重构后的效果较差。

5. 结论

我们从以上的实例的演示中发现，随着码书的数目的增加，可以对重构图像有明显的效果，但是也不是无限增大，会在一定范围达到阈值；同时发现码字的大小也对图像的重构影响也挺大的，码字越小图像越清晰。但是我们也知道，在实验的过程中，我们是零图像自身训练的码本。但是这样在实际应用中是不可取的，因为我都把图像传过去了，还做压缩不是多次一举嘛！所以我们在实际运用时，会选择一种编码端和解码端都知道的数据进行初始化码本。

6. 收获及体会

此次选择图像的矢量量化作为我的研究报告是由于我在学习的过程中是以该章节做报告的，也比较对这部分有兴趣，最终选择利用MATLAB对图像实现进行矢量量化和重构的实验。过程中也出现的大量的问题，比如码本的设计，在参考书本和网上教程，最终实现了这样的一个版本。感觉此次收获还是挺大的，一是对MATLAB程序的编码更加熟悉，二是对代码的调试更加灵活！