计算机视觉——仿射变换、图像扭曲及图像中的图像
单应性变换
原理
图像中的2D点(x,y)(x,y)可以被表示成3D向量的形式(x1,x2,x3)(x1,x2,x3),其中x=x1/x3x=x1/x3,y=x2/x3y=x2/x3。它被叫做点的齐次表达,位于投影平面P2P2上。所谓单应就是发生在投影平面P2P2上的点和线可逆的映射。其它叫法包括射影变换、投影变换和平面投影变换等。
单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。而这里说的平面是指图像或者三维中的平面表面。单应性变换具有很强的实用性,比如图像配准、图像纠正和纹理扭曲,以及创建全景图像。
仿射变换
原理
仿射变换(Affine Transformation 或Affine Map)是一种二维坐标(x, y)到二维坐标(u, v)的线性变换,其数学表达式形式如下:
在这里插入图片描述
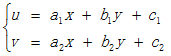
对应的齐次坐标矩阵表示形式为:
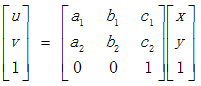
仿射变换保持了二维图形的“平直性”(直线经仿射变换后依然为直线)和“平行性”(直线之间的相对位置关系保持不变,平行线经仿射变换后依然为平行线,且直线上点的位置顺序不会发生变化)。非共线的三对对应点确定一个唯一的仿射变换。
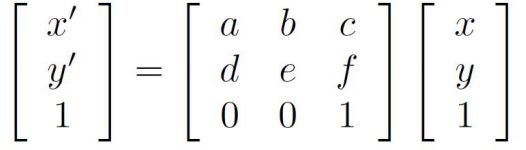
由于仿射变换具有6个自由度,因此我们需要三个对应点来估计矩阵H。通过将最后两个元素设置为0,即h7=h8=0,仿射变换可以用DLT算法估计得出。##
图像扭曲
图像扭曲是图形变化的一种,它可以用于许多场合。
对图像块应用仿射变换,我们将其称为图像扭曲,该操作不仅经常应用在计算机图形学中,而且经常出现在计算机视觉算法中。
from scipy import ndimage
from PIL import Image
from pylab import *
im = array(Image.open('E:/images/ch2/1.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))
figure()
gray()
subplot(121)
axis('off')
imshow(im)
subplot(122)
axis('off')
imshow(im2)
show()
该代码输出的结果如下阿图所示:

从图片中不难看出,输出图像结果中丢失的像素用零来补充。
图像中的图像
图像映射
• 流程
① 针对两张/多张图像提取特征
② 特征匹配
③ 根据图像变换特点,选取合适的变换结构
④ 根据DLT等方法计算变换结构
⑤ 采用正向/逆向映射,利用插值方式实现图像映
射变换。
仿射扭曲的一个简单例子是,将图像或者图像的一部分放置在另一图像中,使得它们能够和指定的区域或者标记物对齐。
# -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
# example of affine warp of im1 onto im2
im1 = array(Image.open('E:/images/2.jpg').convert('L'))
im2 = array(Image.open('E:/images/ch2/11.jpg').convert('L'))
# set to points
#tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])
tp = array([[164,538,540,264],[40,36,405,405],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
上面代码中,使用仿射变换,将im1,放置到im2上,使im1图像的角和tp尽可能的靠近。tp 是齐次表示的,并且按照从左上角逆时针计算的。将一幅图像插入另一幅图像中的坐标值是通过查看绘制的图像(在PyLab图像中,鼠标的坐标显示在图像底部附近)手工确定的。当然,也可以用PyLab类中的ginput()函数获得。

函数Haffine_from_points()会返回给对应点对的最优仿射变换。在上面的例子中,如果图像的透射效果比较弱,那么这种方式会返回比较好的结果,在具有很强透视效应的情况下,我们不能使用同一仿射变换将全部角点变换到它的目标位置。所以,对于三个点,仿射变换可以将一幅图像进行扭曲,使这三对对应点可以完美地匹配上。这是因为,反射变换具有6个自由度,三个对应点可以给出6个约束条件(对于这三个对应点对,x和y坐标必须都要匹配)。所以,可以将图像分为两个三角形,然后对它们分别进行扭曲图像操作。下面是具体实现代码:
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()
这里简单地为每个三角形创建了alpha图像,然后将所有的图像合并起来。这个三角形的alpha图像可以简单地通过检查像素的坐标是否能够写成三角形顶点坐标的凸组合来计算。
最后代码结合:
# -*- coding: utf-8 -*-
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
# example of affine warp of im1 onto im2
im1 = array(Image.open('E:/images/2.jpg').convert('L'))
im2 = array(Image.open('E:/images/ch2/11.jpg').convert('L'))
# set to points
#tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])
tp = array([[164,538,540,264],[40,36,405,405],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()

