【Graph Embedding】Node2Vec:一种有偏的随机游走
1. Introduction
我们今天看的论文是斯坦福大学的同学 2016 年发表于的 ACM 的论文——《node2vec: Scalable Feature Learning for Networks》,到目前为止已经被引用 2600 多次。
在这篇论文中作者提出了一个半监督学习算法——Node2Vec,采用了有偏的随机游走算法并结合 Skip-gram 算法学习 Network Embedding,Node2Vec 可以通过参数设置来控制搜索策略,从而有效的平衡了 Embedding 的同质性和结构有效性。
接下来我们来看一下 Node2Vec 的具体实现。
2. Node2Vec
首先引入用于学习节点 Embedding 的 Skip-gram 算法,并给出目标函数为:
m a x ∑ u ∈ V l o g P r ( N S ( u ) ∣ f ( u ) ) max \; \sum_{u \in V} log \ Pr(N_S(u) | f(u)) \\ maxu∈V∑log Pr(NS(u)∣f(u))
其中,u 为节点, N s ( u ) N_s(u) Ns(u) 为节点 u 通过采样策略 S 得到的邻居, f ( u ) f(u) f(u) 是一个映射矩阵,相当于 Work2Vec 中的输入向量。
为简便起见,我们给出两个假设:
-
条件独立性假设:假设观察一个节点的领域与观察其他节点的领域相互独立,所以我们有:
P r ( N S ( u ) ∣ f ( u ) ) = ∏ n i ∈ N S ( u ) P r ( n i ∣ f ( u ) ) Pr(N_S(u) | f(u)) = \prod_{n_i \in N_S(u)} Pr(n_i | f(u)) \\ Pr(NS(u)∣f(u))=ni∈NS(u)∏Pr(ni∣f(u)) -
特征空间对称型假设:在特征空间中,源节点与邻节点相互对称。所以我们有:
p r ( n i ∣ f ( u ) ) = e x p ( f ( n i ) ⋅ f ( u ) ) ∑ v ∈ V e x p ( f ( v ) ⋅ f ( u ) ) pr(n_i | f(u)) = \frac{exp(f(n_i) \cdot f(u))}{\sum_{v\in V} exp(f(v) \cdot f(u)) } \\ pr(ni∣f(u))=∑v∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u))
基于上面的假设,目标函数改为
m a x ∑ u ∈ V [ − l o g Z u + ∑ n i ∈ N S ( u ) f ( n i ) ⋅ f ( u ) ] max \ \sum_{u\in V}\big[ -logZ_u + \sum_{n_i \in N_S(u)} f(n_i) \cdot f(u) \big] \\ max u∈V∑[−logZu+ni∈NS(u)∑f(ni)⋅f(u)]
其中 $Z_u = \sum_{v \in V} exp(f(u) \cdot f(v)) $ ,由于计算代价昂贵,所以我们用 Negative Sampling 进行优化。
2.1 Search Strategies
由于网络是非线形的,所以我们需要一个策略来为 Skip-gram 提供一个线形的输入。一种常见的策略是通过游走的方式来对于给定源节点 u 的不同邻域进行采样,邻域 N S ( u ) N_S(u) NS(u) 不仅限与邻近的节点,而是与采样策略 S 有关。
在评价网络节点的相似性我们有同质性和结构等价性两个概念。
- 同质性是指同属于一个集群的两个节点更加相似,如下图的节点 S1 和节点 u;
- 结构等价性是指两个具有相似结构的节点更加相似,如下图的节点 S6 和节点 u。
那么为了更能体现出网络的结构性,我们应该是用 BFS 采集还是 DFS 采集?这里可以简单思考一下。
答案是:BFS 可以获得每个节点的邻居,强调的是局部微观视图,所以通过 BFS 采样的网络更能体现网络的局部结构,从而 Embedding 结果更能体现结构性;而 DFS 可以探索更大的网络结构,只有从更高的角度才能观察到更大的集群,所以其 Embedding 结果更能体现同质性。
这个答案是不是与我们的直觉有所相悖?
2.2 Biased Random Walk
我们先给出随机游走的公式:
p ( c i = x ∣ c i − 1 = v ) = { π v x Z i f ( v , x ) ∈ E 0 o t h e r p(c_i = x | c_{i-1} =v) = \left\{ \begin{aligned} &\frac{\pi_{vx}}{Z} \quad if \ (v,x)\in E \\ &0 \quad \quad other \end{aligned} \right. \\ p(ci=x∣ci−1=v)=⎩⎨⎧Zπvxif (v,x)∈E0other
其中, c i c_i ci 表示第 i 次游走, π v x \pi_{vx} πvx 表示节点之间的转移概率,Z 为常数。
如果需要产生有偏的随机游走,一个比较简单的方法是令 π v x = w v x \pi_{vx} = w_{vx} πvx=wvx ,但这样就没法适应不同网络结构,也不能引导我们的程序去探索不同类型的网络邻居。另外这里有偏的随机游走策略应该是统筹 BFS 和 DFS 的,以平衡同质性和结构等价性。
所以我们定义了一个非标准的转移概率 :
π v x = α p q ( t , x ) ⋅ w v x \pi_{vx} = \alpha_{pq}(t,x) \cdot w_{vx} \\ πvx=αpq(t,x)⋅wvx
其中:
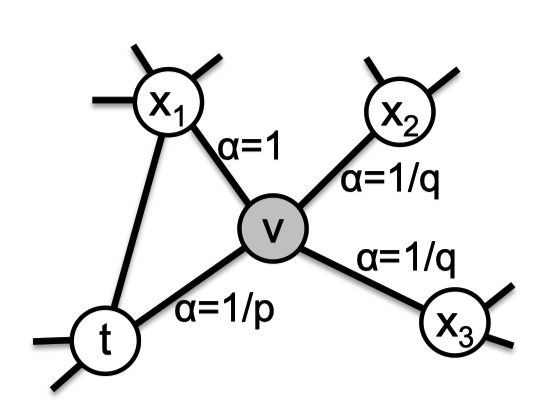
α p q ( t , x ) = { 1 p i f d t x = 0 1 i f d t x = 1 1 q i f d t x = 2 \alpha_{pq}(t,x) = \left\{ \begin{aligned} &\frac{1}{p} \quad if \ d_{tx} = 0 \\ & 1 \quad if \ d_{tx} = 1 \\ & \frac{1}{q} \quad if \ d_{tx} = 2 \end{aligned} \right. αpq(t,x)=⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧p1if dtx=01if dtx=1q1if dtx=2
其中, d t x d_{tx} dtx 表示节点 t 和节点 x 之间的最短路径,取值为 {0, 1, 2}。
我们结合下图来理解:
假设随机游走刚通过节点 t 来到节点 v,现在考虑接下来的转移概率,节点 x 1 x_1 x1 与 节点 t 的最短路径为 1 所以 α = 1 \alpha = 1 α=1,节点 x 2 x_2 x2 与节点 t 的最短路径为 2 所以 α = 1 / q \alpha = 1/q α=1/q ,同理节点 x 3 x_3 x3。
直觉来看,参数 p 和 q 可以用来引导游走,近似地在 BFS 和 DFS 之间穿插,从而反映出不同节点在同质性和结构性上的亲和力。
- Return parameter, p:参数 p 允许搜索程序重新访问遍历过的节点,其值越高,越不可能搜索已访问过的节点;
- In-out parameter, q:参数 q 允许搜索程序区分“向内”和“向外”的节点。如果 q > 1 则,倾向于访问靠近节点 t 的节点,类似于 BFS 策略;反之,倾向于访问远离节点 t 的节点,类似于 DFS 策略。
最初的随机游走算法由于要存储所有的边,所以空间复杂度为 O ( ∣ E ∣ ) O(|E|) O(∣E∣),而有偏置的随机游走空间复杂度为: O ( a 2 ∣ V ∣ ) O(a^2 |V|) O(a2∣V∣) ,其中 a 是网络节点的平均度数,其值通常非常小。
Node2Vec 的随机游走方法兼容了 DFS 和 BFS 的优点,并且具有较低的时间复杂度和空间复杂度。现在我们来看下 Node2Vec 的伪代码:
Node2Vec 的算法共分为三个部分:预处理计算转移概率(PreprocessModifiedWeights,这个可以实现计算好),有偏置的随机游走(Node2VecWalk,加权采样使用的是 Alias 算法,我们在 LINE 那片论文里介绍过这个算法,其事件复杂度为 O(1))和异步随机梯度下降。每个阶段都可以并行化处理,这有助于加速 Node2Vec 算法的训练。
2.3 Learning Edge Feature
这篇文章还有一个创新的地方在于:除了原本的 Embedding 任务还给出了边的预测的任务。对于两个节点 u 和 v,其 Embedding 向量 f ( u ) f ( v ) f(u)\ f(v) f(u) f(v) 可以映射一个新的 Embedding g ( u , v ) g(u, v) g(u,v),例如 $g: V \times V \rightarrow R{d{’}} $ 。其中, d ′ d^{'} d′ 是映射后节点对 (u,v) 的 Embedding 维度。可选的操作有:
3. Experience
来简单看一下实验,对比的实验除了 DeepWalk、LINE 外,还有谱聚类,实验目标是多分类,评价指标为 Macro-F1 和 Micro-F1:
来看下 Node2Vec 关于同质性和结构等价性的效果,下图为 Node2Vec 生成《悲惨世界》共现网络的可视化图,标签颜色可以反映同质性(上)和结构等价性(下)。图片的上半部分参数值为 p=1, q=0.5,图片的下半部分参数值为 p=1, q=2。
再来看下参数敏感性:
最后看一下边的预测:
上图的第一行是一些指标,用于评测数据集,评测方法如下:
4. Conclusion
一句话总结:Node2Vec 是一个新的 NetWork Embedding 算法,其综合 BFS 和 DFS 优缺点,提出了有偏的随机游走算法,最终的实验表明其具有良好的性能和可伸缩性。
从这篇文章中我们可以学到:
- 一种新的 Network Embedding 算法——Node2Vec;
- 有偏的随机游走算法;
- BFS 和 DFS 采样方法带来的结构性和同质性;
- 一种边预测的判定条件。
5. Reference
- 《node2vec: Scalable Feature Learning for Networks》
- 《关于Node2vec算法中Graph Embedding同质性和结构性的进一步探讨》
关注公众号跟踪最新内容:阿泽的学习笔记。
![]()