图像处理------图像锐化(微分法)
取自孙明的"数字图像处理与分析基础"
考察正弦函数sin2 π π ax,它的微分为2 π π acos2 π π ax,微分后频率不变,幅度上升2 π π a倍.空间频率越高,幅值增加就越大.这表明微分可以通过加强高频成分,使图像轮廓变清晰.最常用的微分方法视梯度法.设有一副图像 f(x,y) f ( x , y ) ,它的梯度采用数学概念描述时是一个向量,定义为
可见,梯度具有以下两个重要性质:
- 梯度的方向在函数 f(x,y) f ( x , y ) 最大变化率的方向上.
- 该梯度向量的模为 G[f(x,y)]=[(∂f/∂x)2+(∂f/∂y)2]12 G [ f ( x , y ) ] = [ ( ∂ f / ∂ x ) 2 + ( ∂ f / ∂ y ) 2 ] 1 2
G[f(x,y)] G [ f ( x , y ) ] 称为图像 f(x,y) f ( x , y ) 的梯度,实际上视图像 f(x,y) f ( x , y ) 的梯度图像.
从数学上说,梯度的数值为 f(x,y) f ( x , y ) 在其最大变化率方向上的单位距离所增加的量.对于数学图像,可用差分来近似微分.
几种常见差分算法
(1)梯度算法
按照差分运算近似的梯度表达式为
G[f(x,y)]=[(f(x,y)−f(x+1,y))2+(f(x,y)−f(x,y+1))2]12....(1) G [ f ( x , y ) ] = [ ( f ( x , y ) − f ( x + 1 , y ) ) 2 + ( f ( x , y ) − f ( x , y + 1 ) ) 2 ] 1 2 . . . . ( 1 )
其中,各个像素 f(x,y) f ( x , y ) , f(x+1,y) f ( x + 1 , y ) , f(x,y+1) f ( x , y + 1 ) 之间的位置关系为
| f(x,y) f ( x , y ) | f(x,y+1) f ( x , y + 1 ) |
|---|---|
| f(x+1,y) f ( x + 1 , y ) |
(2)罗伯茨(Roberts)梯度算法
另一种常用的梯度算法称为罗伯茨梯度算法,它是一种交叉差分的计算方法,定义为
G[f(x,y)]=[(f(x,y)−f(x+1,y+1))2+(f(x+1,y)−f(x,y+1))2]12....(2) G [ f ( x , y ) ] = [ ( f ( x , y ) − f ( x + 1 , y + 1 ) ) 2 + ( f ( x + 1 , y ) − f ( x , y + 1 ) ) 2 ] 1 2 . . . . ( 2 )
其中,各个像素 f(x,y) f ( x , y ) , f(x+1,y+1) f ( x + 1 , y + 1 ) , f(x+1,y) f ( x + 1 , y ) , f(x,y+1) f ( x , y + 1 ) 之间的位置关系为
| f(x,y) f ( x , y ) | f(x,y+1) f ( x , y + 1 ) |
|---|---|
| f(x+1,y) f ( x + 1 , y ) | f(x+1,y+1) f ( x + 1 , y + 1 ) |
(3)索伯尔(Sobel)算法
索伯尔算法的差分可表示为
G[f(x,y)]=[d1f(x,y)]2+d2f(x,y)]2−−−−−−−−−−−−−−−−−−−√.........(3) G [ f ( x , y ) ] = [ d 1 f ( x , y ) ] 2 + d 2 f ( x , y ) ] 2 . . . . . . . . . ( 3 )
其中, d1f(x,y)=(a2+ca3+a4)−(a0+ca7+a6) d 1 f ( x , y ) = ( a 2 + c a 3 + a 4 ) − ( a 0 + c a 7 + a 6 ) , d2f(x,y)=(a0+ca1+a2)−(a6+ca5+a4) d 2 f ( x , y ) = ( a 0 + c a 1 + a 2 ) − ( a 6 + c a 5 + a 4 ) ,而 a0 a 0 , a1 a 1 ,……, a7 a 7 之间的位置关系如图1(a)所示, d1 d 1 和 d2 d 2 为图1(b)和(c)所示的模板,其中常数c=2.
| a0 a 0 | a1 a 1 | a2 a 2 |
|---|---|---|
| a7 a 7 | (x,y) ( x , y ) | a3 a 3 |
| a6 a 6 | a5 a 5 | a4 a 4 |
图1(a) a0 a 0 , a1 a 1 ,……, a7 a 7 之间的位置关系
| −1 − 1 | 0 0 | 1 1 |
|---|---|---|
| −c − c | 0 0 | c c |
| −1 − 1 | 0 0 | 1 1 |
图1(b) d1 d 1
| 1 1 | c c | 1 1 |
|---|---|---|
| 0 0 | 0 0 | 0 0 |
| −1 − 1 | −c − c | 1 1 |
图1(b) d2 d 2
上面三图是索伯尔和普瑞维特算法模板
(4)普瑞维特(Prewitt)算法
普瑞维特算法的方程与索伯尔算法相同,只是常数c=1,如图(1)所示.与索伯尔算法方程相同的算法还有Sethi算法,这种算法的常数c=3;以及各向同性索伯尔(Isotropic Sobel)算法,次算法的常数 c=2–√ c = 2 .后者的特点是沿不同方向锐化时梯度幅值一致.
上述采用平方根的算法运算较费时,为更适合计算机实现,采用下面的绝对差分算法.
梯度算法:
G[f(x,y)]≈|f(x,y)−f(x+1,y)|+|f(x,y)−f(x,y+1)| G [ f ( x , y ) ] ≈ | f ( x , y ) − f ( x + 1 , y ) | + | f ( x , y ) − f ( x , y + 1 ) |
罗伯茨梯度算法:
G[f(x,y)]≈|f(x,y)−f(x+1,y+1)|+|f(x+1,y)−f(x,y+1)| G [ f ( x , y ) ] ≈ | f ( x , y ) − f ( x + 1 , y + 1 ) | + | f ( x + 1 , y ) − f ( x , y + 1 ) |
索伯尔和普瑞维特算法:
G[f(x,y)]≈|d1f(x,y)|+|d2f(x,y)| G [ f ( x , y ) ] ≈ | d 1 f ( x , y ) | + | d 2 f ( x , y ) |
(5)拉普拉斯算法(二阶差分)
拉普拉斯算法的差分可表示为
G2[f(x,y)]=Δ21f(x,y)+Δ21f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)……(4) G 2 [ f ( x , y ) ] = Δ 1 2 f ( x , y ) + Δ 1 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) … … ( 4 )
其模板如下图所示,这个模板可作为拉普拉斯1模板,常用的其它拉普拉斯模板入表1所示.
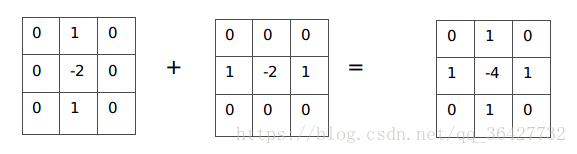
表1如下

(6)LoG算法
LoG边缘检测器的基本特征是,平滑滤波器是高斯滤波器,加强步骤采用二阶差分(拉普拉斯算法).LoG算子的输出是通过卷集运算得到的:
h(x,y)=G2[g(x,y)∗f(x,y)]..................(5) h ( x , y ) = G 2 [ g ( x , y ) ∗ f ( x , y ) ] . . . . . . . . . . . . . . . . . . ( 5 )
根据卷积微分法有:
h(x,y)=[G2g(x,y)]∗f(x,y)..................(6) h ( x , y ) = [ G 2 g ( x , y ) ] ∗ f ( x , y ) . . . . . . . . . . . . . . . . . . ( 6 )
其中
直接实现LoG算法如图3所示,这是一个5*5拉普拉斯高斯模板.

对N*N数字图像,不可能在最后一行(x=N)和最后一列(y=N)像素上计算梯度值.一种补救办法视用前一行(x=N-1)和前一列(y=N-1)对应的像素的梯度值.
某像素上的梯度值视该像素与相邻像素的灰度差值的单调递增函数,具有以下特点:
- 图像轮廓上,像素灰度右陡然变化,梯度值很大.
- 图像灰度 变化平缓区域,梯度值很小.
- 等灰度区域,梯度值为零.
后续会加入scipy库中相关函数处理的程序
未完待续......