acwing算法基础（第四章）高斯消元解线性方程组、组合数、卡特兰数

1.原理：高斯消元

2. 代码实现

#include 
#include 
#include 

using namespace std;

const int N = 110;
const double eps = 1e-6;//浮点数需要判断是否为零

int n;//未知数数量
double a[N][N];//存增广矩阵

//高斯消元函数，三个返回值，分别代表：唯一解，无解，无穷解
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )//比较每行开头数字大小，r从第一行开始处理
    {
        //step1:找到开头的数绝对值最大那一行，并交换
        int t = r;//从第一行开始
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;//找到绝对值最大的，并记录下来是第几行

        if (fabs(a[t][c]) < eps) continue;//如果这个系数为0， 重新执行循环

        //step2:开头的系数化为1
        for (int i = c; i < n + 1; i ++ ) swap(a[t][i], a[r][i]);//交换这两行
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];//除以开头那个数，变为1

        //step3:将下边所有行的对应列变为0
        for (int i = r + 1; i < n; i ++ )//遍历下边所有行
            if (fabs(a[i][c]) > eps)//如果对应列不为0
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];//下边行的每一个系数都加上上一行的某个倍数

        r ++ ;//处理下一行
    }

    //化为阶梯矩阵以后，判断解的情况
    if (r < n)//如果方程数少于未知数的个数
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)//零等于非零，无解
                return 2;
        return 1;//否则无穷多解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[j][n] * a[i][j];

    return 0;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            cin >> a[i][j];

    int t = gauss();

    if (t == 0)
    {
        for (int i = 0; i < n; i ++ ) printf("%.2lf\n", a[i][n]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");

    return 0;
}

3.组合数

#include 
#include 

using namespace std;

const int N = 2010, mod = 1e9 + 7;


int c[N][N];

//stpe1:预处理通过递推算出所有组合
void init()
{
    for (int i = 0; i < N; i ++ )
        for (int j = 0; j <= i; j ++ )
            if (!j) c[i][j] = 1;//如果j==0那么为1
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;//这个地推公式隐含了c12为0，数组建立起来时初始值都为0，正常是不会有c12的
}


int main()
{
    int n;

    init();//预处理，算出所有值

    scanf("%d", &n);//读入要计算的值

    while (n -- )//查表输出
    {
        int a, b;
        scanf("%d%d", &a, &b);

        printf("%d\n", c[a][b]);
    }

    return 0;
}

4.组合数2

预处理出a!与a!的逆元（用于做除法） 

#include 
#include 

using namespace std;

typedef long long LL;//两个1e9相乘会溢出long，所以定义Long long

const int N = 100010, mod = 1e9 + 7;


int fact[N], infact[N];


int qmi(int a, int k, int p)//求逆元
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int main()
{
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++ )//遍历N个数
    {
        fact[i] = (LL)fact[i - 1] * i % mod;//a!=(a-1)!*a,LL转换类型
        infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;//求逆元
    }//求出了所有阶乘和其逆元
    

    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);//组合公式
    }

    return 0;
}

 5.组合数3

卢卡斯定理

#include 
#include 

using namespace std;

typedef long long LL;


int qmi(int a, int k, int p)//快速幂
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}


int C(int a, int b, int p)//方法二中的求解方法
{
    if (b > a) return 0;

    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}


int lucas(LL a, LL b, int p)//卢卡斯定理
{
    if (a < p && b < p) return C(a, b, p);//如果小于p，用方法二
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;//如果大于p用卢卡斯
}


int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        LL a, b;
        int p;
        cin >> a >> b >> p;
        cout << lucas(a, b, p) << endl;
    }

    return 0;
}

6.组合数4 

题目要求高精度

#include 
#include 
#include 

using namespace std;


const int N = 5010;

int primes[N], cnt;
int sum[N];
bool st[N];


void get_primes(int n)//筛质数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)//n中含P的个数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector mul(vector a, int b)//高精度乘法
{
    vector c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }
    return c;
}


int main()
{
    int a, b;
    cin >> a >> b;

    get_primes(a);

    for (int i = 0; i < cnt; i ++ )
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(a - b, p) - get(b, p);
    }

    vector res;
    res.push_back(1);

    for (int i = 0; i < cnt; i ++ )
        for (int j = 0; j < sum[i]; j ++ )
            res = mul(res, primes[i]);

    for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
    puts("");

    return 0;
}

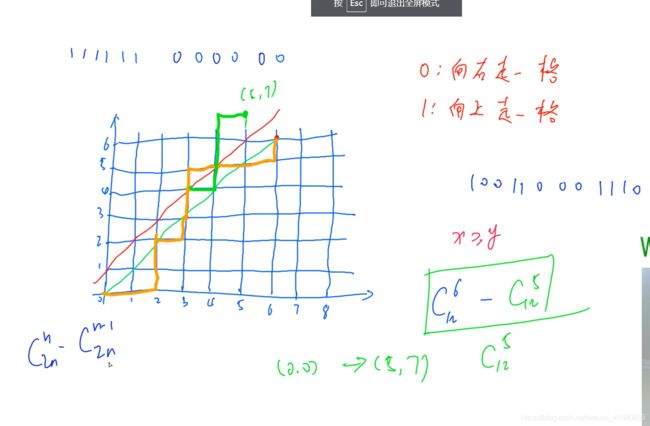
7.卡特兰数 

 方案数与路径数一样

 所有从（0，0）到（6，6）并且经过红线的路径，都对应于一条从（0，0）到（5，7）的路径，所以不合法路径数为c(12,5)。

（5，7）为（6，6）关于绿线的轴对称点。