一文弄懂算法的时间和空间复杂度分析

前言

一般来说，解决问题的方法不止一种。我们需要学习如何比较不同算法的性能，并选择最佳算法来解决特定的问题。一个算法的好坏，我们可以从时间和空间两个维度去衡量。并且，一般分为两个阶段，一是算法完成前的理论分析，二是算法完成后实际分析。

• 理论分析：这种算法的效率分析是通过假设所有其他因素，如处理器的速度等是恒定的，对算法的实现没有影响。
• 实际分析：当算法实现后，我们需要考虑算法采用编程语言，然后在特定计算机上执行该算法，其消耗的时间与计算机的硬件水平相关。在此分析中，我们要收集实际的统计数据，如运行时间和所需空间。

本篇文章要讨论的主要是算法的理论分析，从常见的时间、空间复杂度入手，介绍各种时间、空间复杂度的特点，并总结一些通用数据结构、排序算法、搜索算法相关操作的时间和空间复杂度。最后，针对递归操作，使用Master Theorem来分析其复杂度。

时间、空间复杂度简介

时间复杂度

时间复杂度是指执行这个算法所需要的计算工作量，其复杂度反映了程序执行时间随输入规模增长而增长的量级，在很大程度上能很好地反映出算法的优劣与否。一个算法花费的时间与算法中语句的执行次数成正比，执行次数越多，花费的时间就越多。一个算法中的执行次数称为语句频度或时间频度，记为T(n)，其中n称为问题的规模，当n不断变化时，它所呈现出来的规律，我们称之为时间复杂度。比如：$T(n)=n^2+1$与$T(n)=5n^2+2n+1$，虽然算法的时间频度不一样，但他们的时间复杂度却是一样的，时间复杂度只关注最高数量级，且与之系数也没有关系。通常一个算法由控制结构（顺序，分支，循环三种）和原操作（固有数据类型的操作）构成，而算法时间取决于两者的综合效率。

空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，所谓的临时占用存储空间指的就是代码中辅助变量所占用的空间，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。我们用 S(n)=O(f(n))来定义，其中n为问题的规模(或大小)。通常来说，只要算法不涉及到动态分配的空间，以及递归、栈所需的空间，空间复杂度通常为0(1)。一个一维数组a[n]，空间复杂度O(n)，二维数组为O(n^2)。

大O表示法

大O符号是由德国数论学家保罗·巴赫曼（Paul Bachmann）在其1892年的著作《解析数论》（Analytische Zahlentheorie）首先引入的。算法的复杂度通常用大O符号表述，定义为T(n) = O(f(n))。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。 如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时，时间复杂度的极限情形称为算法的“渐近时间复杂度”。空间复杂度同理。举个例子，令$f(n)=2n^2+3n+5$，$O(f(n))=O(2n^2+3n+5)=O(n^2)$。

时间、空间复杂度计算方法

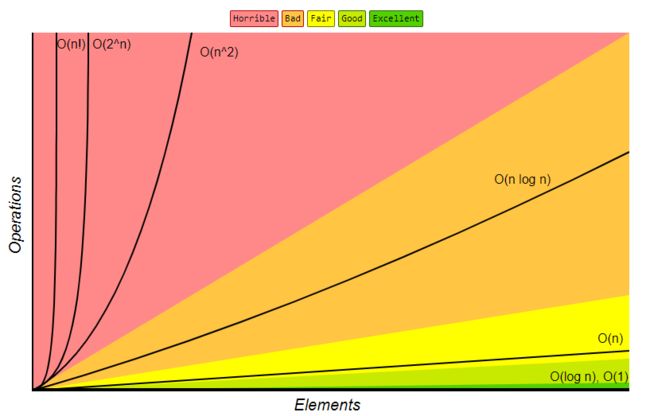
如图展示了几种常见的复杂度形式：非常糟糕的复杂度有O(n!)，O(2^n)，O(n^2)；比较糟糕的有O(nlog n)，可以接受的有O(n)，还不错的有O(n)，非常好的有O(logn)和O(1)。

如何计算时间复杂度

如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为O(1)，如

a = 1
b = 2
c = a + b
b += a

一个循环，算法需要执行的运算次数用输入大小n的函数表示，即 T(n) 。下面这个函数，语句频度T(n) = 2 + 2*n + 1，那么时间复杂度为O(2*n + 3) = O(n)，因为时间复杂度只关注最高数量级，且与之系数也没有关系。

def fun(n):
    count1 = 0
    count2 = 0
    for i in range(n):
        count1 += 1
        count2 += 2
    return count

对于多个循环，假设循环体的时间复杂度为O(n)，各个循环的循环次数分别是a, b, c…，则这个循环的时间复杂度为 O(n×a×b×c…)。分析的时候应该由里向外分析这些循环。比如下面这个函数，复杂度为O(n*n*1) = O(n^2)

def fun(n):
    count = 0
    for i in range(n):
        for j in range(n):
            count += 1
    return count

对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度。比如下面这个函数，第1部分复杂度为O(n^2)，第2部分复杂度为O(n)，总复杂度为max(O(n^2), O(n)) = O(n^2)

def fun(n):
    # 第1部分复杂度为O(n^2)
    count = 0
    for i in range(n):
        for j in range(n):
            count += 1
    # 第2部分复杂度为O(n)
    for i in range(n):
        count += 2
    return count

对于条件判断语句，总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。当n >= 0分支的复杂度最大，即总复杂度为O(n^2)

def fun(n):
    if n >= 0:
        # 第1部分复杂度为O(n^2)
        count = 0
        for i in range(n):
            for j in range(n):
                count += 1
    else:
        # 第2部分复杂度为O(n)
        for i in range(n):
            count += 2
    return count

总结：时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数调用，就要深入函数进行分析。

如何计算空间复杂度

我们在写代码时，完全可以用空间来换取时间，比如字典树，哈希等都是这个原理。算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地"进行的，是节省存储的算法，空间复杂度为O(1)，注意这并不是说仅仅定义一个临时变量；有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如将快速排序和归并排序算法就属于这种情况。

如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1)。如下代码中的 i、j、t 所分配的空间都不随着处理数据量变化，因此它的空间复杂度为O(1)。

i = 0
j = 1
t = i + j

这段代码中，第一行定义了一个列表，这个列表的长度随着n的规模不同，会不一样，这里空间复杂度为O(n)。

def fun(n):
    temp = []
    for i in range(n):
        temp.append(i)

对于一个算法，其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；反之，追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。另外，算法的所有性能之间都存在着或多或少的相互影响。因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。

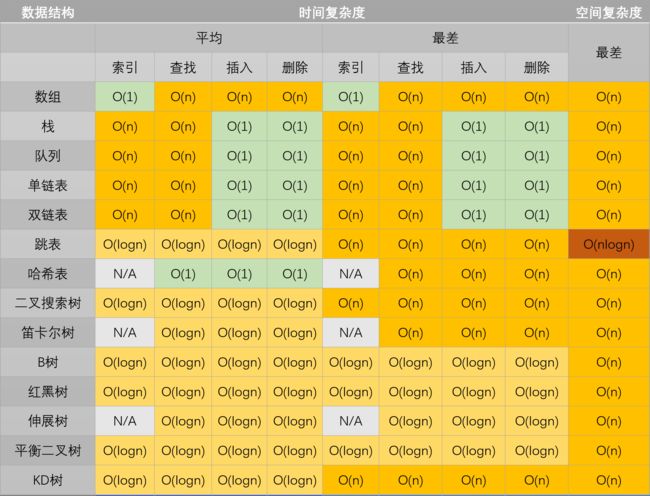
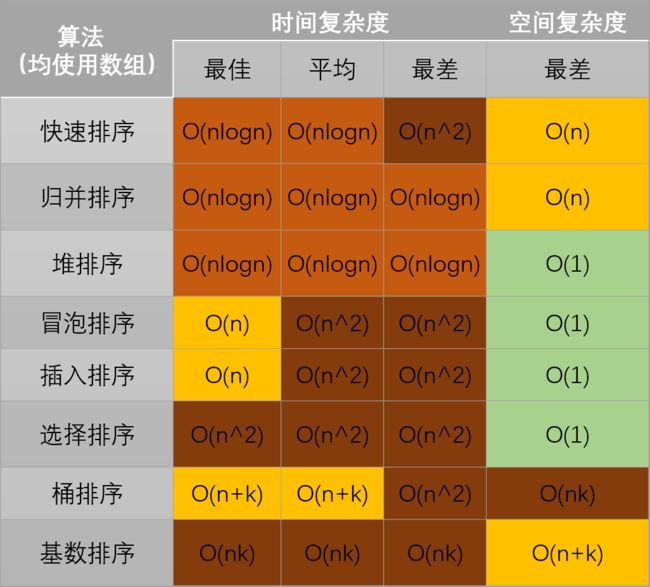
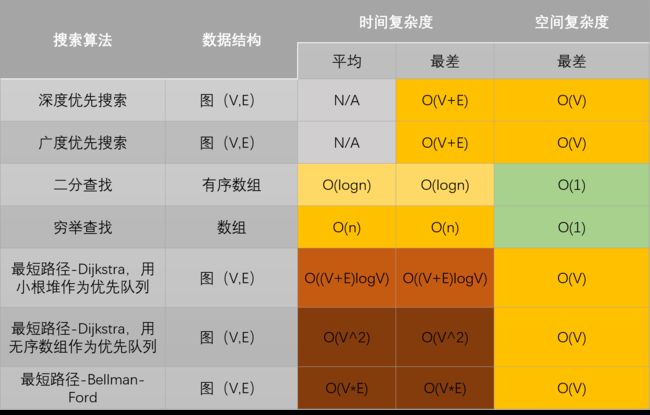
常见数据结构与算法的时间、空间复杂度总结

数据结构

堆

图

排序算法

搜索算法

Master Theorem解决递归复杂度求解

Master Theorem提供了用大O符号表示许多由分治法得到的递推关系式的方法。其基本形式如下，
$$T\left(n\right)=aT\left(\frac{b}{n}\right)+f\left(n\right),a⩾\text{1 }andb>1$$
其中$n$表示问题规模，$a$为递推的子问题数量，$\frac{b}{n}$为每个子问题的规模（假设每个子问题的规模基本一样），$f(n)$为递推以外进行的计算工作。
具体怎么用呢，当我们根据分析，得到算法T(n)的表达式后，则根据以下步骤确定最终的时间复杂度：

• 根据T(n)，分别确定$a$, $b$和$f(n)$；
• 决定$n^{{\log }_{b}a}$;
• 比较$n^{{\log }_{b}a}$和$f(n)$；
• 匹配到以下三种情况，得到最终复杂度。

我们可以分三种情况进行讨论：

当运行时间主要由leaves决定

如果存在常数$\epsilon >0$，有$f(n)=O\left(n^{{\log }_b(a)-\epsilon }\right),$则$T(n)=O\left(n^{{\log }_{b}a}\right)$。

举例：$T\left(n\right)=9T\left(\frac{n}{3}\right)+n$

• $a=9$, $b=3$, $f(n)=n$;
• $n^{{\log }_{b}a}=n^2$;
• $n^{{\log }_{b}a}>f(n)$;
• 匹配到运行时间主要由leaves决定，得到$T\left(n\right)=O\left(n^{{\log }_{b}a}=n^2\right)$

当运行时间均匀分布在整个树中

如果存在常数$\epsilon ⩾0$，有$f\left(n\right)=O\left(n^{{\log }_{{}_b}a}{\log }^{\epsilon }n\right)$，则$T\left(n\right)=O\left(n^{{\log }_{{}_b}a}{\log }^{\epsilon +1}n\right)$。

举例：$T\left(n\right)=2T\left(\frac{n}{2}\right)+n$

• $a=2$, $b=2$, $f(n)=n$;
• $n^{{\log }_{b}a}=n$;
• $n^{{\log }_{b}a}=f(n)$;
• 匹配到运行时间均匀分布在整个树中，得到$T\left(n\right)=O\left(n^{{\log }_{2}2}{\log }^{0+1}n\right)=O\left(n\log n\right)$

当运行时间主要由root决定

如果存在常数$\epsilon >0$，有$f\left(n\right)=\Omega \left(n^{{\log }_{{}_b}\left(a\right)+\epsilon }\right)$，同时存在$c<1$以及充分大的$n$，满足$af\left(\frac{n}{b}\right)⩽cf\left(n\right)$，则$T\left(n\right)=O\left(f(n)\right)$。

举例：$T\left(n\right)=3T\left(\frac{n}{4}\right)+nlog(n)$

• $a=3$, $b=4$, $f(n)=nlog(n)$;
• $n^{{\log }_{b}a}=n^{{\log }_{4}3}$;
• $n^{{\log }_{b}a}<f(n)$;
• 匹配到运行时间主要由root决定，检查条件，发现存在$c=\frac{3}{4}$，满足$af\left(\frac{n}{b}\right)⩽cf\left(n\right)$，即$3\cdot \frac{n}{4}\log \frac{n}{4}⩽\frac{3}{4}\cdot n\log n$，得到$T\left(n\right)=O\left(f\left(n\right)\right)=O\left(n\log n\right)$

---

欢迎关注我的公众号“野风同学”，一个程序员的自我成长之路，持续分享机器学习、NLP、LeetCode算法和Python等技术干货文章，同时也经常推荐高质量软件工具、网站和书籍。