我今天大概的也只是了解了线段树, 但是对于他的应用场景, 什么时候使用, 也大概清楚了, 但是运用上应该是差点意思, 真正用这个算法解315题, 我是没看懂, 谁要是可以研究明白, 请多多赐教!
举例: 假设有一个数组 array[0... n-1], 里面有n个元素, 现在要经常对这个数组做两个事情.
-
更新数组元素的数值
- 求数组任意一段区间里元素的总和(或者平均值)
解法1: 遍历一遍数组. 时间复杂度O(n)
解法2: 线段树
-
线段树, 就是一种按照二叉树的形式存储数据的结构, 每个节点保存的都是数组里某一段的总和.
-
适用于数据很多, 而且需要频繁更新并求和的操作
- 时间复杂度O(logn)
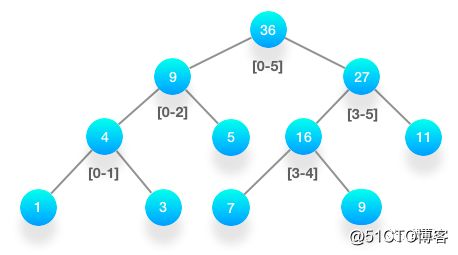
举例: 数据是[1, 3, 5, 7, 9, 11], 那么它的线段树如下:
根节点保存的是从下标 0 到下标 5 的所有元素的总和,即 36。左右两个子节点分别保存左右两半元素的总和。按照这样的逻辑不断地切分下去,最终的叶子节点保存的就是每个元素的数值。
解法:
1.更新数组里某个元素的数值
从线段树的根节点出发,更新节点的数值,它保存的是数组元素的总和。修改的元素有可能会落在线段树里一些区间里,至少叶子节点是肯定需要更新的,所以,要做的是从跟节点往下, 判断元素的下标是否在左边还是右边, 然后更新分支里的节点大小. 因此, 复杂度就是遍历树的高度, 即O(logn)
对于数组某个区间段的元素进行求和
方法和更新操作类似, 首先从根节点触发, 判断所求的区间是否落在节点代表的区间中, 如果所要求的区间完全包含了节点锁代表的区间, 那么就得加上该节点的数值, 意味着该节点所记录的区间总和只是所有求解总和的一部分, 接下来, 不断的往下寻找其他的子区间, 最终的处所要求的总和.
例题分析
leetcode 315题
15.计算右侧小于当前元素的个数](https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/)
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质:counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.1. 暴利解法
暴力模拟法思路非常简单,就是每次都从末尾找比num[i]小的数并计数,然后放到结果数组即可
vector countSmaller(vector& nums) {
int n=nums.size();
vectorans(n,0);
int t;
for(int i=n-2;i>=0;i--){
t=0;
for(int j=n-1;j>i;j--){
if(nums[j] 2. 对方法一进行一些优化
我们从暴力模拟法为起点进一步优化,我们看到每次我们都要从末尾遍历相同的元素,实际上我们可以建立一个保持排序的数组sorted_num。这个数组代表:在nums[i]之后所有的数,并且已经排好序。
每次在nums数组出现新的需要判断的数就要插入到这个sorted_num,然后在这个数通过二分查找到下界(可以用STL自带的lower_bound()) 减去sorted_num.begin()就是比nums[i]小的元素个数了。
这个题目我是在官网没有找到最好的解法, 如何使用现状树来解此题,我也没有看明白, 希望大家来给我解惑, 我是真的菜啊.以上的两种方法, 仅仅是我能想到的解题思路, 其他的就真的不行了,
大佬的解法, 谁能看懂, 给我讲讲啊!