前缀树

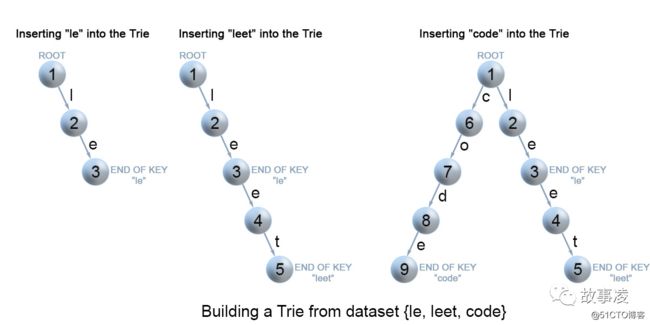
今天刷算法题, 前缀树, 字典树, 真的是一个好东西啊, 在思想上又给自己打开了一个新的思路啊!
前缀树被广泛的运用在字典查找中, 也被称为字典树

举例: 给定一系列字符串, 这些字符串构成了一种字典, 要求你在这个字典当中找出所有以"ABC"开头的字符串

解法一: 暴利搜索

直接遍历一遍字典, 然后逐个判断每个字符串是否由"ABC"开头, 假设字典很大, 有N个单词, 要对比的不是"ABC", 而是任意的, 那不妨假设所要对比的开头平均长度为M, 那么时间复杂度是O(M x N)

解法二: 前缀树

如果用前缀树头帮助对字典的存储进行优化, 那么可以把搜索的时间复杂度下降为O(M), 其中M表示字典里最长的那个单词的字符个数, 很多情况下, 字典里的单词个数N是远远大于M的, 因此, 前缀树在各种场合中是非常高效的.

经典应用

---

1. 网站的搜索框会罗列出以搜索文字作为开头的相关搜索信息, 这里运用了前缀树进行后端的快速检索

2. 汉字拼音输入法的联想输出功能也是运用了前缀树

Trie (发音为 "try") 或前缀树是一种树数据结构，用于检索字符串数据集中的键。这一高效的数据结构有多种应用：

1. 自动补全

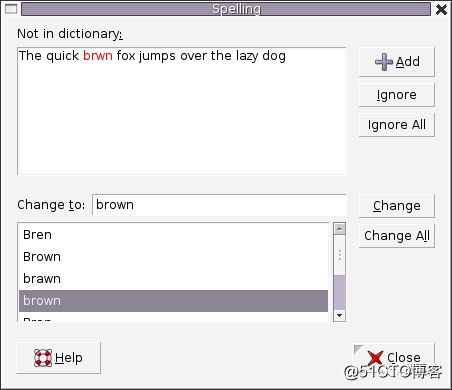
2. 拼写检查

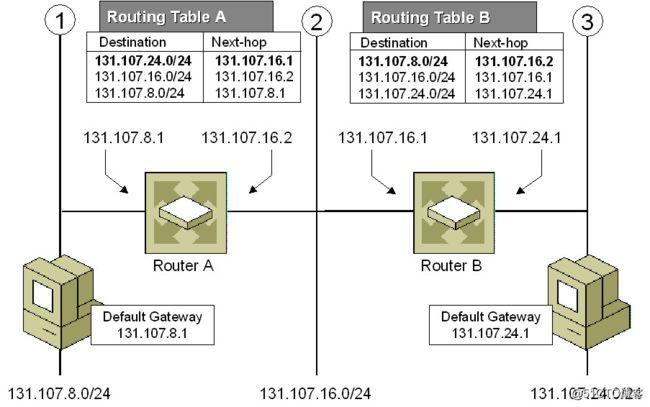
3. IP路由(最长前缀匹配)

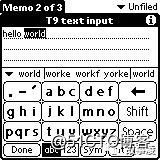
4. T9(九宫格) 打字预测

5. 单词游戏

还有其他的数据结构，如平衡树和哈希表，使我们能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢？尽管哈希表可以在 O(1)O(1) 时间内寻找键值，却无法高效的完成以下操作：

• 找到具有同一前缀的全部键值。

• 按词典序枚举字符串的数据集。

Trie 树优于哈希表的另一个理由是，随着哈希表大小增加，会出现大量的冲突，时间复杂度可能增加到 O(n)O(n)，其中 nn 是插入的键的数量。与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 O(m)O(m) 的时间复杂度，其中 mm 为键长。而在平衡树中查找键值需要 O(m \log n)O(mlogn) 时间复杂度。

Trie 树的结点结构

Trie 树是一个有根的树，其结点具有以下字段：。

• 最多 RR 个指向子结点的链接，其中每个链接对应字母表数据集中的一个字母。本文中假定 RR 为 26，小写拉丁字母的数量。

• 布尔字段，以指定节点是对应键的结尾还是只是键前缀。

前缀树的java代码:

class TrieNode {

   // R links to node children
// 连接到 R 条子节点
   private TrieNode[] links;

   // 最初只有26个字符, 最多有26条子节点
   private final int R = 26;

// 判断是否是一个单词是否结束
   private boolean isEnd;

  // 构造器, 初始化的时候, 都要创建26子节点
   public TrieNode() {
       links = new TrieNode[R];
  }

   // 判断子节点是否存在, ch - 'a' 是0-25
   public boolean containsKey(char ch) {
       return links[ch -'a'] != null;
  }
   // 获取到子节点
   public TrieNode get(char ch) {
       return links[ch -'a'];
  }
   // 往子节点中放元素
   public void put(char ch, TrieNode node) {
       links[ch -'a'] = node;
  }
   // 设置为单词的结束符
   public void setEnd() {
       isEnd = true;
  }
   // 获取单词的结束符
   public boolean isEnd() {
       return isEnd;
  }
}

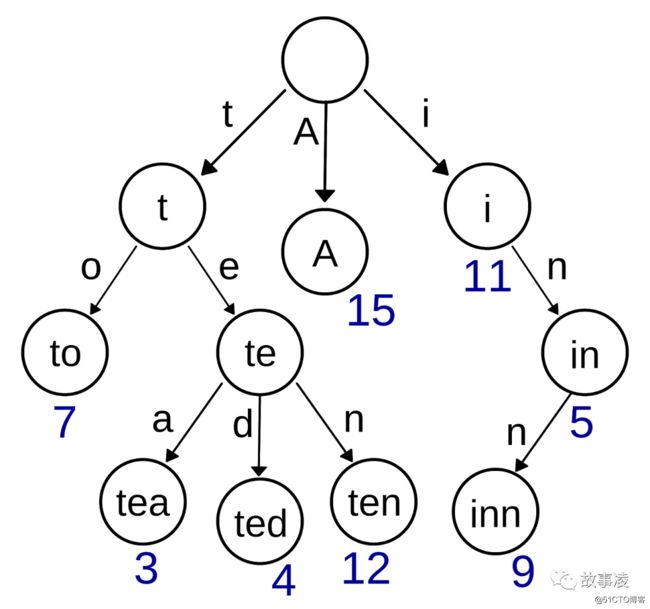
举例: 假如有一个字典, 字典里面有下面词: "A", "to", "tea", "ted", "ten", "i", "in", "inn", 每个单词还能有自己的一些权重值, 那么用前缀树来构建这个字典将会是如下的样子:

性质

1. 每个节点至少包含两个基本属性

   • Childern: 数组或者集合, 罗列出每个分支当中包含的所有字符

   • idEnd, 布尔值, 表示是该节点是否为某字符串的结尾
2. 前缀树的根节点是空的

所谓空, 即只利用这个节点的children属性, 即只关心在这个字典里, 有哪些打头的字符

1. 除了根节点, 其他所有节点都有可能是单词的结尾, 叶子节点一定都是单词的结尾

实现

前缀叔最基本的操作就是两个: 创建和搜索

1. 创建

遍历一遍输入的字符串, 对每个字符串的字符进行遍历

从前缀的根节点开始, 将每个字符加入到节点的children字符集当中.

如果字符集已经包含了这个字符, 则跳过

如果当前字符是字符串的最后一个, 则把当前节点的isEnd标记为真.

由上, 创建的方法很直观

前缀树真正强大的地方在于, 每个每个节点还能用来保存额外的信息, 比如可以用来记录拥有相同前缀的所有字符串, 因此, 当用户输入某个前缀时, 就能在O(1)的时间内给出对应的推荐字符串

我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况：

链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。链接不存在。创建一个新的节点，并将它与父节点的链接相连，该链接与当前的键字符相匹配。重复以上步骤，直到到达键的最后一个字符，然后将当前节点标记为结束节点，算法完成。

向前缀树中插入元素:

class Trie {
   private TrieNode root;

   public Trie() {
       root = new TrieNode();
  }

   // Inserts a word into the trie.
   public void insert(String word) {
       TrieNode node = root;
       for (int i = 0; i < word.length(); i++) {
           // 获取到每个字符
           char currentChar = word.charAt(i);
           // 判断是否存在, 不存在, 直接放入子节点
           if (!node.containsKey(currentChar)) {
               node.put(currentChar, new TrieNode());
          }
           // 子节点变成父节点, 进行下一次的循环
           node = node.get(currentChar);
      }
       // 设置最后的字符为单词的结束符
       node.setEnd();
  }
}

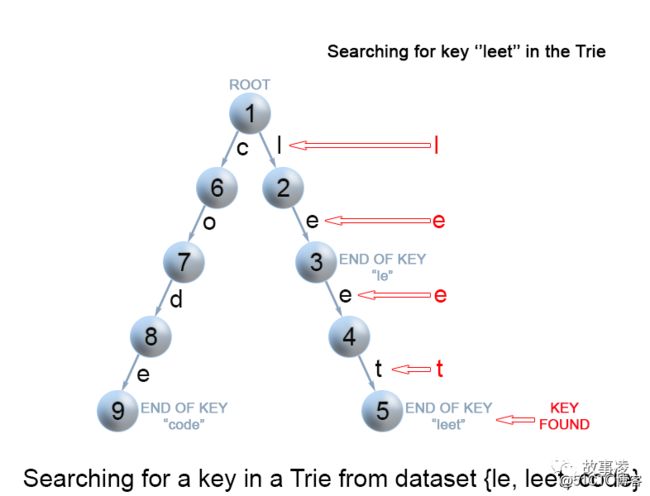
2. 搜索

与创建方法类似, 从前缀的根节点出发, 逐个匹配输入的前缀字符, 如果遇到了就继续往下一层搜索, 如果没遇到, 就立即返回.

在 Trie 树中查找键每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始，。检查当前节点中与键字符对应的链接。有两种情况：

存在链接。我们移动到该链接后面路径中的下一个节点，并继续搜索下一个键字符。不存在链接。若已无键字符，且当前结点标记为 isEnd，则返回 true。否则有两种可能，均返回 false :还有键字符剩余，但无法跟随 Trie 树的键路径，找不到键。没有键字符剩余，但当前结点没有标记为 isEnd。也就是说，待查找键只是Trie树中另一个键的前缀。

在树中查找元素

class Trie {
  ...

   // search a prefix or whole key in trie and
   // returns the node where search ends
   // 搜索前缀
   private TrieNode searchPrefix(String word) {
       TrieNode node = root;
       for (int i = 0; i < word.length(); i++) {
          // 获取到单词的每一个字符
          char curLetter = word.charAt(i);
          // 如果子节点包含, 就把子节点当成新的父节点, 进入下一次循环
          if (node.containsKey(curLetter)) {
              node = node.get(curLetter);
          } else {
            // 否则, 就返回空
              return null;
          }
      }
       // 返回最终的子节点
       return node;
  }

   // Returns if the word is in the trie.
   // 判断单词是否存在于前缀树中
   public boolean search(String word) {
      TrieNode node = searchPrefix(word);
      // 最后的节点不能为空, 而且该节点上必须有单词的结束符
      return node != null && node.isEnd();
  }
}

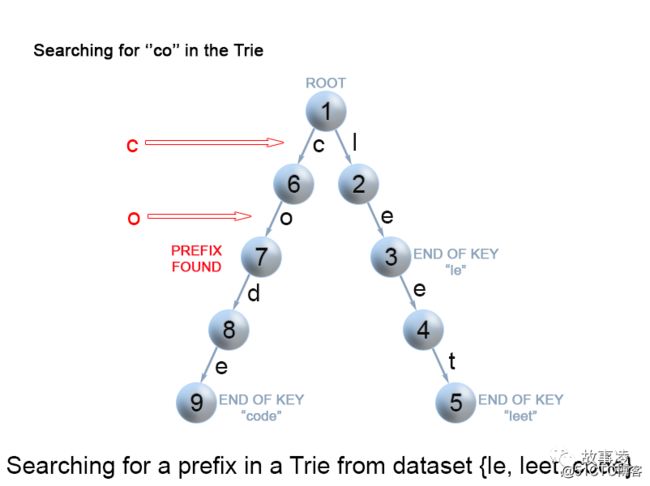
查找 Trie 树中的键前缀该方法与在 Trie 树中搜索键时使用的方法非常相似。我们从根遍历 Trie 树，直到键前缀中没有字符，或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是，到达键前缀的末尾时，总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记，因为我们搜索的是键的前缀，而不是整个键。

class Trie {
  ...

   // Returns if there is any word in the trie
   // that starts with the given prefix.
   public boolean startsWith(String prefix) {
       TrieNode node = searchPrefix(prefix);
       return node != null;
  }
}

例题分析

---

12.单词搜索 II](https://leetcode-cn.com/problems/word-search-ii/)
给定一个二维网格 board 和一个字典中的单词列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例:

输入:
words = ["oath","pea","eat","rain"] and board =
[
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]

输出: ["eat","oath"]

说明:你可以假设所有输入都由小写字母 a-z 组成。

提示:

你需要优化回溯算法以通过更大数据量的测试。你能否早点停止回溯？如果当前单词不存在于所有单词的前缀中，则可以立即停止回溯。什么样的数据结构可以有效地执行这样的操作？散列表是否可行？为什么？前缀树如何？如果你想学习如何实现一个基本的前缀树，请先查看这个问题：实现Trie（前缀树）。

import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Set;

public class findWords_212 {
   public List findWords(char[][] board, String[] words) {
       //构建字典树
       wordTrie myTrie=new wordTrie();
       trieNode root=myTrie.root;
       for(String s:words)
           myTrie.insert(s);

       //使用set防止重复
       Set result =new HashSet<>();
       int m=board.length;
       int n=board[0].length;
       boolean[][] visited=new boolean[m][n];
       //遍历整个二维数组
       for(int i=0;i(result);
  }
   private void find(char [] [] board, boolean [][]visited,int i,int j,int m,int n,Set result,trieNode cur){
       //边界以及是否已经访问判断
       if(i<0||i>=m||j<0||j>=n||visited[i][j])
           return;
       cur=cur.child[board[i][j]-'a'];
       visited[i][j]=true;
       if(cur==null)
      {
           //如果单词不匹配，回退
           visited[i][j]=false;
           return;
      }
       //找到单词加入
       if(cur.isLeaf)
      {
           result.add(cur.val);
           //找到单词后不能回退，因为可能是“ad” “addd”这样的单词得继续回溯
//           visited[i][j]=false;
//           return;
      }
     //上下左右去遍历, 通过递归的方法去实现
       find(board,visited,i+1,j,m,n,result,cur);
       find(board,visited,i,j+1,m,n,result,cur);
       find(board,visited,i,j-1,m,n,result,cur);
       find(board,visited,i-1,j,m,n,result,cur);
       //最后要回退，因为下一个起点可能会用到上一个起点的字符
       visited[i][j]=false;
  }

}

//字典树
class wordTrie{
   public trieNode root=new trieNode();
   public void insert(String s){
       trieNode cur=root;
       for(char c:s.toCharArray()){
           if(cur.child[c-'a']==null){
               cur.child [c-'a'] = new trieNode();
               cur=cur.child[c-'a'];
          }else
               cur=cur.child [c-'a'];
      }
       cur.isLeaf=true;
       cur.val=s;
  }
}
//字典树结点
class trieNode{
   public String val;
   public trieNode[] child=new trieNode[26];
   public boolean isLeaf=false;

   trieNode(){

  }
}

故事凌
明天能否加个鸡腿！
钟意作者