【梳理】离散数学 第15章 欧拉图与哈密顿图 15.1 欧拉图 15.2 哈密顿图

教材：《离散数学》第2版 屈婉玲 耿素云 张立昂 高等教育出版社
源文档高清截图在最后

第15章欧拉图与哈密顿图

15.1 欧拉图

1、通过图中所有边仅一次的通路称作欧拉通路。通过图中所有边仅一次的回路称作欧拉回路。具有欧拉回路的图是欧拉图，仅具有欧拉通路的图是半欧拉图。平凡图（只含一个顶点的图）是欧拉图。

2、无向图G是欧拉图，当且仅当G是连通图且没有奇度顶点。
证明 若G为平凡图，显然成立。设该图G(V, E)为非平凡图，具有m条边和n个顶点。
必要性（左推右）。因为G为欧拉图，所以G存在欧拉回路C。对任意vi, vj∈V，vi, vj都在C上。因而vi, vj连通，G为连通图。对任意vi∈V，vi在C上每出现一次就获得两个度（一个入度和一个出度），而所有顶点都会出现在C中至少一次，于是G中无奇度顶点。
充分性（右推左）。由于G为非平凡的连通图，边数m≥1，下面对m作归纳证明。
m = 1时，因为G没有奇度顶点，但G又是连通的，所以G只能是一个环。G为欧拉图。
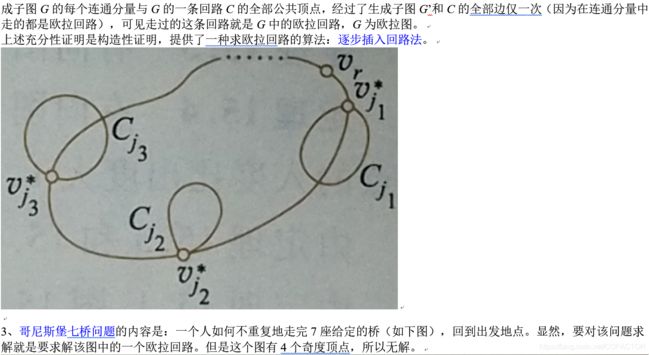
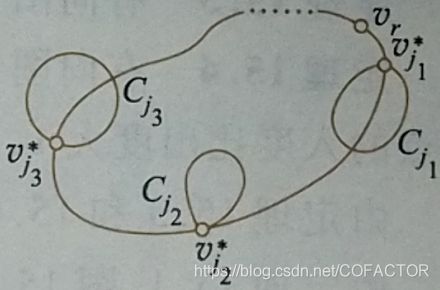
如果m≤k（k≥1）时结论都成立，那么m = k + 1时结论也要成立。由于G的连通性且无奇度顶点，G的最小度δ(G)≥2。可以证明G中必含圈。设C为G中的一个圈，将删除C中的全部边以后剩下的部分记为G的一个生成子图G’。设G’有s个连通分量G1’、G2’、……、Gs’，其中每个连通分量最多有k条边，且无奇度顶点。设Gi’与C的公共顶点为，i = 1，2，……，s。由归纳假设，G1’、G2’、……、Gs’都是欧拉图，它们都存在欧拉回路。设Ci是Gi’的一条欧拉回路，i = 1，2，……，s。从某个顶点vr开始沿C行走，遇到就行遍Ci，回到继续沿C行走，最后回到vr。于是，走过的这条回路借由G的生成子图G的每个连通分量与G的一条回路C的全部公共顶点，经过了生成子图G’和C的全部边仅一次（因为在连通分量中走的都是欧拉回路），可见走过的这条回路就是G中的欧拉回路，G为欧拉图。
上述充分性证明是构造性证明，提供了一种求欧拉回路的算法：逐步插入回路法。

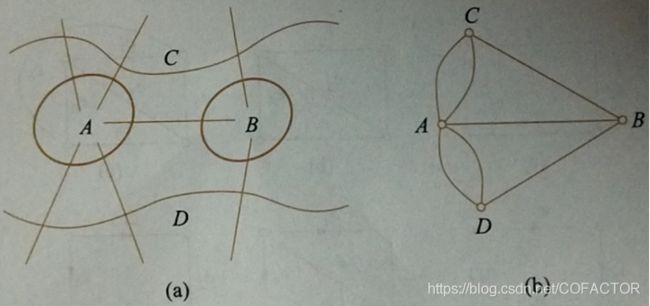
3、哥尼斯堡七桥问题的内容是：一个人如何不重复地走完7座给定的桥（如下图），回到出发地点。显然，要对该问题求解就是要求解该图中的一个欧拉回路。但是这个图有4个奇度顶点，所以无解。

4、无向图G是半欧拉图，当且仅当G是连通的且恰有2个奇度顶点。
证明 必要性（左推右）。设该图G(V, E)是m条边的n阶无向图。因为G为半欧拉图，所以G存在欧拉通路但不存在欧拉回路。设该欧拉通路为Γ = vi0ej1vi1ej2…ejmvim，且vi0≠vim。根据欧拉图的定义，G是连通的。对任意v∈V，如果v不是Γ的端点，设其出现k次，那么就有v的度d(v) = 2k。如果v是Γ的端点，由于两个端点不同且不相邻，v作为端点就只能出现1次，获得1度。当v是端点时，它还可能作为非端点继续出现若干次，每次获得2度。所以d(v)是奇数。
充分性（右推左）。设G的两个奇度顶点u、v，对G加新边(u, v)，得G’ = G∪(u, v)。则G连通且无奇度顶点。于是G为欧拉图，存在欧拉回路C’。C = C’ – (u, v)就是G中的欧拉通路，G为欧拉图。

5、对有向图，可类似证明定理：
【1】有向图D是欧拉图，当且仅当D是强连通的，且每个顶点的入度等于出度。
【2】有向图D是半欧拉图，当且仅当D是单向连通的，且恰有两个奇度顶点：其中一个顶点的入度比出度大1，另一个的出度比入度大1，其余顶点的入度等于出度。

6、G是非平凡的欧拉图，当且仅当G是连通的，且是若干个边不重的圈的并图。
可用归纳法证明。

7、设G是非平凡的欧拉图，则G的边连通度λ(G)≥2。
证明 只需证明G不是1边-连通图。即证G的任意一条边e都不是桥（割边，去掉该边后图不再连通）。设C是一条欧拉回路，那么e在C上，且G – e的连通分支（连通分量）数p(G – e) = p(G)，故e不是桥。

8、Fleury算法
用途：求欧拉回路。
基本思想：能不走桥就不走桥。
输入：欧拉图G(V, E)。
1、任取v0∈V，记P0 = v0，i = 0。
2、设Pi = v0e1v1e2…eivi，如果E – {e1，e2，……，ei}没有与vi关联的边，计算停止。否则，按下述条件从E – {e1，e2，……，ei}中任取边ei+1:
(a) ei+1与vi关联；
(b)除非没有别的边可以选择，否则不应该为Gi = G – {e1，e2，……，ei}中的桥。
3、i = i + 1，返回到第2步。
算法停止时，得到的简单回路Pm = v0e1v1e2…emvm为G的一条欧拉回路。

15.2 哈密顿图

1、经过图的所有顶点仅一次的通路称为哈密顿通路，经过图中所有顶点仅一次的回路称作哈密顿回路。具有哈密顿回路的图称作哈密顿图，具有哈密顿通路但不具有哈密顿回路的图称作半哈密顿图。
（从起点出发和到达终点不算经过）
平凡图是哈密顿图。目前人们还没有找到便于判断哈密顿图的充分必要条件。

2、设无向图G(V, E)是哈密顿图，则对任意的非空集，均有p(G – V1)≤|V1|。
证明 设C为G中的一条哈密顿回路。易知，当V1中的点在C上均不相邻（虽然V1的点都在C上，但两两不由一条边直连）时，p(C – V1)达到最大值|V1|（连通分量最大，即分成了尽可能多的互不连通的子图。删掉V1及其关联的边后，最多可以构造出|V1|个互不连通的子图。一种构造方法是：从起点开始依次给点编号（0或1开始均可），V1是全部编号为奇数的点）。而当V1的点在C上存在相邻情况时，总有p(C – V1) < |V1|。所以p(C – V1)≤|V1|。C是G的生成子图，所以p(G – V1)≤p(C – V1)≤|V1|。
本定理给出的是判定一个图是哈密顿图的必要条件，而不是充分条件。Peterson图满足该条件，但它不是哈密顿图。
推论 设无向图G(V, E)是半哈密顿图，则则对任意的非空集，均有p(G – V1)≤|V1| + 1。
证明 设P是G中从u到v的哈密顿通路，G’为在u，v之间加新边e得到的图，易知添加该边以后哈密顿通路变成哈密顿回路，G’为哈密顿图。于是p(G’ – V1)≤|V1|。而p(G – V1) = p(G’ – V1 – e)≤p(G’ – V1) + 1≤|V1| + 1。（提示：G – V1和G’ – V1 – e是完全相同的图，G’ – V1去掉e后可能会因为e是割边（桥）从而连通分量数 + 1）

3、设G是n阶无向简单图，若对G中任意不相邻顶点u，v，均有d(u) + d(v)≥n – 1，则G中存在哈密顿通路。
证明 （我也没搞懂，日后再更）一个图是哈密顿图首先要是连通图。设G不连通，则G至少有2个连通分量G1、G2。设u、v分别是G1、G2的一个顶点，因为G是简单图，所以（一个点的度最大的情况是该点与图中其它点都有边直连），矛盾，所以G是连通图。
下面证明G中存在哈密顿通路。设Γ = v1v2…vl为G中的一条极大路径，即Γ的起点与终点都不与Γ外的顶点相邻，l≤n。
（1）若l = n，则Γ就是G中的哈密顿通路，定理成立。
（2）若l < n，则G存在Γ外的顶点，要证明G中存在过Γ上所有顶点的圈：
【a】若v1与vl相邻，则Γ∪(v1, vl)就是这个圈。
【b】若v1与vl不相邻，设v1与Γ上的vi1 = v2，vi2，……，vik相邻（k≥2，否则d(v1) + d(vl)≤1 + l – 2≤l – 1 < n – 1，与已知条件d(u) + d(v)≥n – 1不符。因为l < n，所以d(vl)≤l – 2，因为vl至少与1个点不相邻）。vl至少与vi2，vi3，……，vik相邻的顶点之一相邻（否则d(v1) + d(vl)≤k + l – 2 – (k – 1) = l – 1 < n – 1，与已知条件d(u) + d(v)≥n – 1不符）。设vl与相邻（2≤r≤k），于是回路经过Γ上的所有顶点。
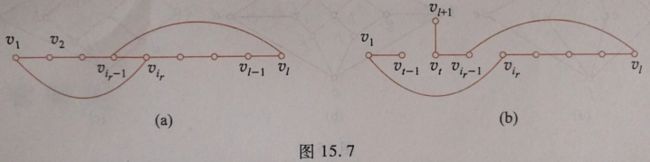
【c】下面证明存在比Γ更长的路径。因为l < n，所以C外还有顶点。由G是连通的，得存在vi+1∈V(G) – V©与C上的某个顶点vt相邻，当t < ir – 1时，删除边(vt-1, vt)得路径比Γ的长度大1。当t≥ir – 1时，可类似构造出比Γ的长度大1的路径Γ’。重复【a】到【c】，在有限步内一定可以得到G的一条哈密顿通路。

推论 设G为不少于3阶的无向简单图，若对于G中任意两个不相邻顶点u，v均有d(u) + d(v)≥n，则G中存在哈密顿回路。
证明 由上述定理，G中存在一条哈密顿通路Γ = v1v2…vn。若v1与vn相邻，就将这条边e添加到Γ中，就得到G的一条哈密顿回路Γ∪e。若不相邻，可以仿照上述的证明方法证明存在过Γ上各个顶点的圈，此圈就是哈密顿回路。

4、设u、v为n阶无向简单图G的两个不相邻顶点，且d(u) + d(v)≥n，则G为哈密顿图，当且仅当G∪(u, v)是哈密顿图，其中(u, v)是添加的新边。

5、不低于2阶的竞赛图都有哈密顿通路。
回忆：若有向图D的基图（有向边全部改成无向边后的图）为n阶无向完全图，就称D为n阶竞赛图。
证明 设D为n阶竞赛图，对n归纳证明。
当n = 2时，D的基图是二阶完全图K2，结论成立。
设n = k时结论成立，那么n = k + 1时结论也要成立。设V(D) = {v1, v2, …, vk, vk+1}，记D1 = D – vk+1，易知D1为k阶竞赛图。由归纳假设，D1存在哈密顿通路Γ1 = v1’v2’…vk’。下面，需要证明vk+1可以加入Γ 1中。若存在vr’（1≤r≤k）使(vi’, vk+1)、(vk+1, vr’)∈E(D)，i = 1，2，……，r – 1。则可以得到哈密顿通路Γ = v1’v2’…vr-1’vk+1vr’…vk’。若不存在，则任意i = 1，2，……，k，均有(vi’, vk+1)∈E(D)，则可以得到哈密顿通路Γ = v1’v2’…vk’vk+1。