《离散数学》第三章：命题逻辑（第一部分）

3.1什么是命题

3.1.1命题和非命题

注意：数理逻辑研究的中心问题是推理，而推理的前提和结论都是命题。因而命题是推理的基本 单位。

定义：具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”，称为真值。真值只有 “真”和“假”两种，分别用“T”(或“1”) 和“F”(或“0”)表示。

注意：一切没有判断内容的句子，如命令句 (或祈使句)、感叹句、疑问句、二义性的陈述句等都不 能作为命题。

3.1.2复合命题（如何产生新命题）

定义：

（1）原子命题 (简单命题)：不能再分解为更为 简单命题的命题。

（2）复合命题：可以分解为更为简单命题的命 题。这些简单命题之间是通过如“或 者”、“并且”、“不”、“如果...... 则......”、“当且仅当”等这样的关联词和标 点符号复合而成。

约定：通常用大写的带或不带下标的英文字母表示命题 (包括原子命题和复合命题)。 A,B,C,· · · ,P,Q,R,· · · , Ai,Bi,Ci,· · · ,Pi,Qi,Ri,· · ·

3.2命题联结词

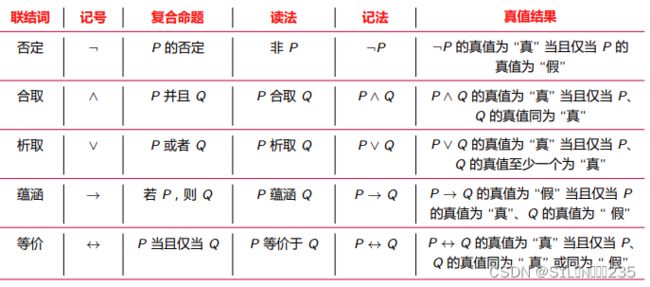
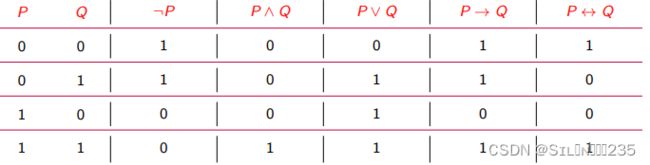
3.2.1 否定联结词

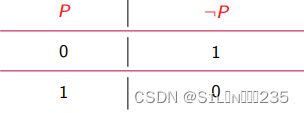
定义：设 P 是任意一个命题，复合命题“非 P”(或 “P 的否定”)称为 P 的否定式(negation)，记作¬P， “¬” 为否定联结词。P 为真当且仅当 ¬P 为假。

”¬” 是自然语言中的 “非”、“不”、“没有” 等的逻辑抽象。

3.2.2合取联结词

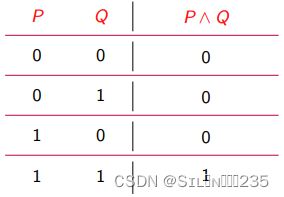
定义：设 P、Q 是任意两个命题，复合命题“P 并且 Q”(或 “P 和 Q”)称为 P 与 Q 的合取 式(conjunction)，记作P ∧ Q，“∧” 为合取联结词。P ∧ Q 为真当且仅当 P，Q 同为真。

注意 “∧” 是自然语言中的 “并且”、“既…又…”、“但”、“和”、“与”、“不仅…而且…”、“虽然…但 是…”、“一面…, 一面…” 等的逻辑抽象；但不是所有的“和”，“与”都要使用合取联结词 表示，要根据句子的语义进行分析。

3.2.3析取联结词

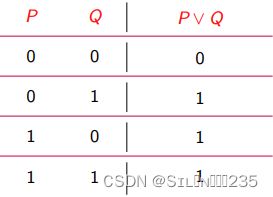
定义：设 P、Q 是任意两个命题，复合命题“P 或 Q”称为 P 与 Q 的析取式(disjunction)，记作P ∨ Q， “∨” 为析取联结词。P ∨ Q 为真当且仅当 P，Q 至少有一个为真。

注意 联结词 “∨” 是自然语言中的 “或”、“或者” 等的逻辑抽象。自然语言中的 “或” 有 “可兼 或”(或称为同或)、“不可兼或”(即异或) 两种。严格来讲，析取联结词实际上代表的是可兼 或，异或有时会使用单独的异或联结词 “⊕” 或 “∨¯” 来表示。

3.2.4蕴涵联结词

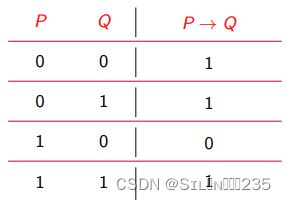
定义：设 P、Q 是任两个命题，复合命题“如果 P，则 Q”称为 P 与 Q 的蕴涵式(implication)，记 作P → Q，“→” 为蕴涵联结词。P → Q 为假当且仅当 P 为真且 Q 为假。一般把蕴涵式 P → Q 中的 P 称为该蕴涵式的前件，Q 称为蕴涵式的后件。

注意 在自然语言中，前件为假，不管结论真假，整个语句的意义，往往无法判断。但对于数理 逻辑中的蕴涵联结词来说，当前件 P 为假时，不管 Q 的真假如何，则 P → Q 都为真。此 时称为 “善意推定”。

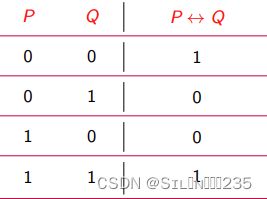
3.2.5等价联结词

定义：Definition 设 P、Q 是任两个命题，复合命题“P 当且仅当 Q”称为 P 与 Q 的等价式(equivalence)，记 作P ↔ Q，“↔” 为等价联结词(也称作双条件联结词)。P ↔ Q 为真当且仅当 P、Q 同为真假

“↔” 是自然语言中的 “等价”、“充分必要条件”、“当且仅当” 等的逻辑抽象。

3.3命题符号化及应用

命题联接词 “∧”、“∨”、“↔” 具有对称性，而 “¬”、“→” 没有。

3.3.1命题联结词的真值表

联结词是两个命题真值之间的联结，而不是命题内容之间的连接，因此复合命题的真值只取决于 构成他们的各简单命题的真值，而与它们的内容无关，与二者之间是否有关系无关。

3.3.2命题联结词的优先级

优先级顺序

1 所有五个联接词的优先顺序为：否定，合取，析取，蕴涵，等价；

2 同级的联结词，按其出现的先后次序 (从左到右)；

3 若运算要求与优先次序不一致时，可使用括号；同级符号相邻时，也可使用 括号。括号中的运算为最高优先级。

3.3.3命题联接词与网页检索

布尔检索

在布尔检索中，联接词 “∧”（一般用 AND 表示）用于匹配包含两个检索项的记 录，联接词 “∨”（一般用 OR 表示）用于匹配包含两个检索项至少一个的记录， 而联接词 “¬”（一般用 NOT 表示）用于排除某个特定的检索项。

3.3.4命题联接词与位运算

位运算

计算机中的信息采用二进制的方式来表达。每个二进制位只能是 1 或 0，可对应于某一 个布尔变量的真值。当我们需要判断该布尔变量的真值时，就可以利用按位与（bitwise AND）或按位或（bitwise OR）以及按位取反（bitwise NOT）等来操作。

3.4命题公式和真值表

3.4.1命题变元

定义

一个特定的命题是一个常值命题，它不是具有值 “T”(“1”)，就是具有值 “F”(“0”)。

定义

一个任意的没有赋予具体内容的原子命题是一个变量命题，常称它为命题变量 (或命题变 元)(propositional variable)，该命题变量无具体的真值，它的变域是集合{T, F}(或 {0, 1})。

复合命题是由原子命题与联结词构成的命题。所以，当其中的原子命题是命题变元时，此 复合命题也即为命题变元的函数，且该函数的值仍为“真”或“假”值，这样的函数可形 象地称为“真值函数” 或 “命题公式”，此命题公式没有确切的真值。 例如：G = P ∧ Q → ¬R

3.4.2命题公式

定义

命题演算的合式公式 (well formed formula，wff)，又称命题公式 (简称公式)，按如下规则生成：

1 命题变元本身是一个公式；（如：P, Q, R, · · · ）

2 如 G 是公式，则(¬G)也是公式；（如：¬P, ¬Q, ¬R, · · · ）

3 如 G，H 是公式，则(G ∧ H)、(G ∨ H)、(G → H)、(G ↔ H)也是公式；（如： P ∧ Q,(¬Q) → R, · · · ）

4 仅由有限步使用规则 (1)、(2)、(3)后所得到的包含命题变元、联结词和括号的符号串才是命 题公式. （

如：¬(P ∧ Q) ↔ R,(¬Q ∨ (P ∧ ¬R)) → R, · · · ）

如果 G 是含有 n 个命题变元 P1、P2、P3、· · · 、Pn 的公式，可记为：G(P1, P2, P3, · · · , Pn) 或简 写为 G

3.4.3关于命题公式的说明

1 原子命题变元是最简单的合式公式，称为原子合式公式，简称原子公式；

2 命题公式没有真值，只有对其命题变元进行真值指派后，方可确定命题公式的真值；

3 整个公式的最外层括号可以省略；公式中不影响运算次序的括号也可以省略。

4 在实际应用中，为了便于存储和运算，命题公式常用二元树的方式来表达。

3.4.4公式的解释

定义

设 P1、P2、P3、· · · 、Pn 是出现在公式 G 中的所有命题变元，指定 P1、P2、P3、· · · 、Pn 一组真 值，则这组真值称为 G 的一个解释，常记为 I。

如果公式 G 在解释 I 下是真的，则称I 满足 G，此时 I 是 G 的成真赋值；如果 G 在解 释 I 下是假的，则称I 弄假于 G，此时 I 是 G 的成假赋值

3.4.5真值表

一般来说，若有 n 个命题变元，则应有 2^n 个不同的解释。

利用真值表，可得到公式的所有成真赋值和成假赋值。

定义：由公式 G 在其所有可能的解释下所取真值构成的表，称为 G 的真值表(truth table)。

真值表画法 ：一般我们将公式中的命题变元放在真值表的左边，将公式的结果放在真值表的右边。有时 为了清楚起见，可将求公式的中间结果也放在真值表中。

3.5公式的分类和逻辑等价

3.5.1命题公式分类

定义：

公式 G 称为永真公式(重言式,tautology)，如果在它的所有解释之下其真值都为“真”。

公式 G 称为永假公式(矛盾式,contradiction)，如果在它的所有解释之下其真值都为“假”。 有时也称永假公式为不可满足公式。

公式 G 称为可满足公式(satisfiable)，如果它不是永假的。

三种特殊公式之间的关系

1 G 是永真的当且仅当 ¬G 是永假的；

2 G 是可满足的当且仅当至少有一个解释 I，使 G 在 I 下为真。

3 若 G 是永真式，则 G 一定是可满足式，但反之可满足公式不一定是永真式；

3.5.2公式的等价

定义 ：设 G，H 是两个命题公式，P1，P2，P3，· · · ，Pn是出现在 G，H 中所有的命题变元，如果对于 P1，P2，P3，· · · ，Pn 的 2 n 个解释，G 与 H 的真值结果都相同，则称公式 G 与 H 是等价的， 记作G = H。（或G ⇔ H）

3.5.3公式等价的充分必要条件

定理：对于任意两个公式 G 和 H，G = H 的充分必要条件是公式 G ↔ H 是永真公式。

证明：

必要性：假定 G = H，则 G，H 在其任意解释 I 下或同为真或同为假，于是由 “↔” 的意义 知，公式 G ↔ H 在其任何的解释 I 下，其真值为“真”，即 G ↔ H 为永真公式。

充分性：假定公式 G ↔ H 是永真公式，I 是它的任意解释，在 I 下，G ↔ H 为真，因此， G，H 或同为真，或同为假，由于 I 的任意性，故有 G = H。

命题公式的可判定性

可判定性: 能否给出一个可行方法，完成对任意公式的判定类问题。（类型或等价判定） 命题公式是可判定的。

3.6基本等价关系及其应用

3.6.1基本等价关系

定理：

设 G, H, S 为任意的命题公式。

1 E1 : G ∨ G = G; (幂等律 )

E2 : G ∧ G = G.

2 E3 : G ∨ H = H ∨ G; (交换律 )

E4 : G ∧ H = H ∧ G.

3 E5 : G ∨ ( H ∨ S) = ( G ∨ H ) ∨ S; (结合律 )

E6 : G ∧ ( H ∧ S) = ( G ∧ H ) ∧ S.

4 E7 : G ∨ 0 = G; (同一律 )

E8 : G ∧ 1 = G.

5 E9 : G ∨ 1 = 1; (零律)

E10 : G ∧ 0 = 0.

6 E11 : G ∨ (H ∧ S) = (G ∨ H) ∧ (G ∨ S); (分配律)

E12 : G ∧ (H ∨ S) = (G ∧ H) ∨ (G ∧ S).

7 E13 : G ∨ (G ∧ H) = G; (吸收律)

E14 : G ∧ (G ∨ H) = G.

8 E15 : ¬G ∧ G = 0. (矛盾律)

9 E16 : ¬G ∨ G = 1. (排中律)

10 E17 : ¬(¬G) = G. (双重否定律)

11 E18 : ¬(G ∨ H) = ¬G ∧ ¬H; (德摩根律)

E19 : ¬(G ∧ H) = ¬G ∨ ¬H.

12 E20 : G → H = ¬G ∨ H. (蕴涵式)

13 E21 : G → H = ¬H → ¬G. (假言易位)

14 E22 : G ↔ H = (G → H) ∧ (H → G) = (¬G ∨ H) ∧ (¬H ∨ G). (等价式)

15 E23 : G ↔ H = ¬G ↔ ¬H. (等价否定等式)

16 E24 : (G → H) ∧ (G → ¬H) = ¬G. (归谬论)