带通配符的字符串匹配问题的动态规划算法

字符串匹配问题，给定一串字符串，按照指定规则对其进行匹配，并将匹配的结果保存至output数组中，多个匹配项用空格间隔，最后一个不需要空格。

要求：

1.        匹配规则中包含通配符?和*，其中?表示匹配任意一个字符，*表示匹配任意多个（>=0）字符。

2.        匹配规则要求匹配最大的字符子串，例如a*d,匹配abbdd而非abbd,即最大匹配子串。

3.        匹配后的输入串不再进行匹配，从当前匹配后的字符串重新匹配其他字符串。

 

我们先考虑rule是否匹配input某一个前缀的情况的情况

相关动态规划算法如下：

设状态dp[i][j]为rule[i]与input[j]是否匹配（true或false）

分别考虑rule[i]==?,*以及普通字符的情况

rule[i]='*'时:

1.      dp[i][j-1]==true能推出di[i][j]==true但是dp[i][j-1]==false不能推出dp[i][j]==false(考虑rule[0...i]=abc*和input[0...j-1]=ab且input[j]=c。所以不能用dp[i][j-1]

2.      应该用dp[i-1][j]和dp[i-1][j-1]。其实是一样的，因为dp[i-1][k]=true即可推出dp[i][j]=true（其中0<=k<=j）。否则就是false。即dp[i][j]与dp[i-1][k]的或等价。

rule[i]='?'时:

1.      dp[i][j-1]和dp[i-1][j]都不能推断出dp[i][j]。比如dp[i][j-1]=ture时，如果rule[0…i]都是普通字符，则明显dp[i][j]=false。但是如果rule[0…i]=*时，则明显dp[i][j]也是true。同理dp[i-1][j]也不能（分别考虑rule[0…i-1]是普通字符串和是*的情况）

2.      dp[i-1][j-1]与dp[i][j]是无条件等价的，可以分别考虑dp[i-1][j-1]=true或false的情况。

 

rule[i]为普通字符时:

1．  同rule[i]==’?’一样，无法通过dp[i][j-1]和dp[i-1][j]推断出dp[i][j]

2．  (dp[i-1][j-1]&&rule[i]==input[j])与dp[i][j]等价。

 

设rule，input都从1开始：

初始化：

dp[0][1….j_len]=flase

dp[1…i_len][0]=false

dp[0][0]=true.

 

动态规划递归式为：

1.      rule[i]==’*’:dp[i][j]=(dp[i-1][k]的或，k=0…j)

2.      rule[i]!=’*’:dp[i][j]=(dp[i-1][j-1]&&(rule[i]==input[j]||rule[i]=’?’))

 

 

从该题得到的思考：

动态规划的递归式需要是充分必要条件：

 

充分：

即当满足递归式时，一定能给出正确的结果。在该题中，即当rule=’?’且dp[i-1][j-1]=ture时dp[i][j]一定是ture。

 

必要性：

所有结果都能通过该递归式得到，不能有遗漏。即完备性。

动态规划的完备性其实很好证明，比如在本题中，只要考虑rule[i]的3种可能取值和将dp[i][j]表填满就行了。即rule=’?’时，虽然dp[i][j-1]和dp[i-1][j]不能用，但是可以通过dp[i-1][j-1]就可以得出结果，加上初始化的值，就可以得出整个dp表的值。

 

以上是快速判断rule是否与input匹配的算法。但是题目其实是要知道rule是否与input的某一子段匹配，一个方法就是遍历以input[0]到input[len]开头的所有子串。即在外面再加一层循环。复杂度是（rule_len）*(input_len)^2。

 

但是其实改一下状态设置就可以直接用动态规划解决。

 

相关动态规划算法如下：

设状态dp[i][j]为rule[0…i]匹配以input[j]结尾的input字符串的最大长度

分别考虑rule[i]==?,*以及普通字符的情况如上

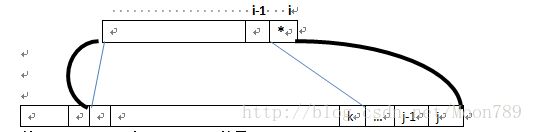
rule[i]='*'时:

  

  若dp[i-1][k]!=-1,则dp[i-1][k]+j-k就是dp[i][j]

当然，得从众多的k中选一个最大的，即dp[i][j]=max{dp[i-1][k]+j-k,0<=k<=j且dp[i-1][k]!=-1}

 

rule[i]='?'时:

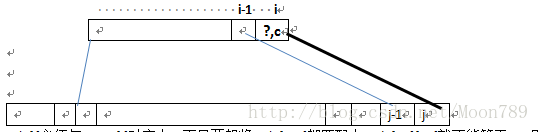
rule[i]为普通字符时:

  rule[i]必须与input[j]对应上，而且要想将rule[0…i]都匹配上，dp[i-1][j-1]就不能等于-1，即必须匹配。

即dp[i-1][j-1]!=1且rule[i]与input[j]匹配（rule[i]==input[j]||rule[i]=’?’）

 

设rule，input都从1开始：

初始化：

dp[0][1….j_len]=0

dp[1…i_len][0]=-1

dp[0][0]=0

 

动态规划递归式为：

3.      rule[i]==’*’:dp[i][j]=max(dp[i-1][k]+j-k)0<=k<=j且dp[i-1][k]!=-1)

4.      rule[i]!=’*’:dp[i][j]=(dp[i-1][j-1]!=-1&&(rule[i]==input[j]||rule[i]=’?’))?dp[i-1][j-1]+1:-1;

 

 

其中初始化的dp[0][1….j_len]=0很重要。例如rule=”n”，input=”nsn”。当n匹配到nsn的第二个n时，就是求dp[1][3]时，要看dp[0][2]，如果dp[0][2]=-1,则意味着rule中n字母之前的就已经不匹配，所以该n也不能匹配。但是很明显，n之前没有字母需要匹配，即要把dp[0][0…len]这种特殊情况摘出来。即不需要考虑之前是否匹配（因为不需要），从新开始匹配。