A* Search Algorithm
A* Search Algorithm
写在前面:第一次写博客,以后想把遇到的有意思的算法或者小知识记录下来。纯原创,部分图片来自课堂PPT,出自UCR,CS170课件。转载请声明出处。
算法简介
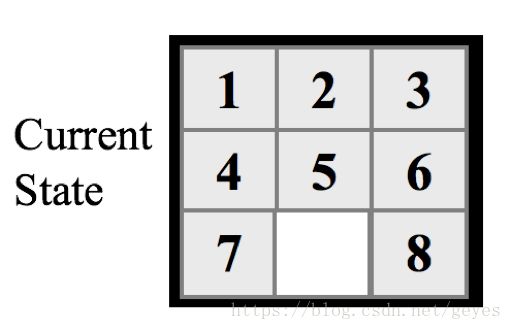
A* Search 是一种启发式搜索算法,该算法内置一个函数来表达当前状态和目标状态的差值。举个栗子,8-puzzle问题(一个游戏,目标是将对应数字的版块放到对应位置)。当前状态是下图
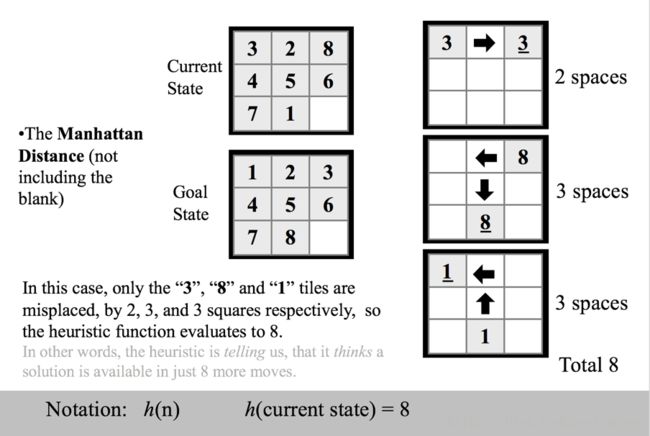
目标状态:
如果我们以两个状态有多少不符合启发函数,那么这里的启发函数的值是
1(PS:这里我们排除了空白格,图中当前态和目标态就一个‘8’不同)
接下来会详细介绍A算法并以8-puzzle游戏左右一个例子来说明该算法,在引入A search前,我会先简单介绍两个算法,Uniform Cost Search和Hill climbing Search。启发函数选择的是Manhattan距离,详解看下图。(h(n)就是启发函数)
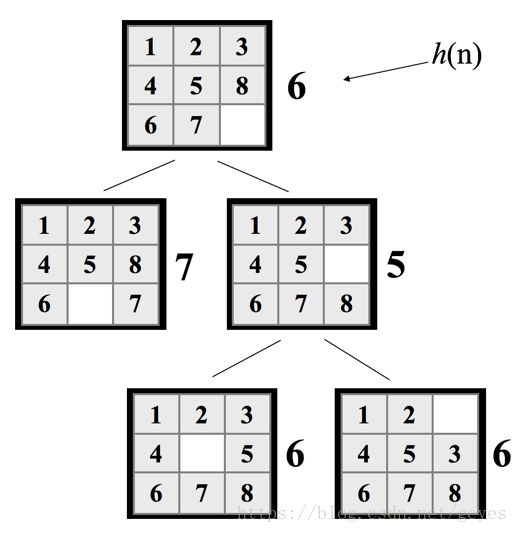
先说说Hill climbing Search,该算法也是一种启发式搜索算法,思路很简单,直接使用Manhattan距离。在下面的例子中,这个算法运行的很好。(h(n)是启发函数)
这个算法运行的很快,可是会遇到问题。有时候该算法在一些状态会陷入找不到解的状态
另一种Uniform Cost Search算法,该算法更简单每次在拓展节点的时候,拓展最廉价的点(该点的耗费是到这个点的路径的累积消耗,拓展累积消耗最小的点)。该算法运行效率较低,但是可以保证每次找到一个解。
背景介绍完毕。接下来进入A*算法,这个算法结合了Uniform Cost Search和Hill climbing Search。将到达该节点的累积消耗g(n)和该节点到达目标节点的差h(n)作为启发函数
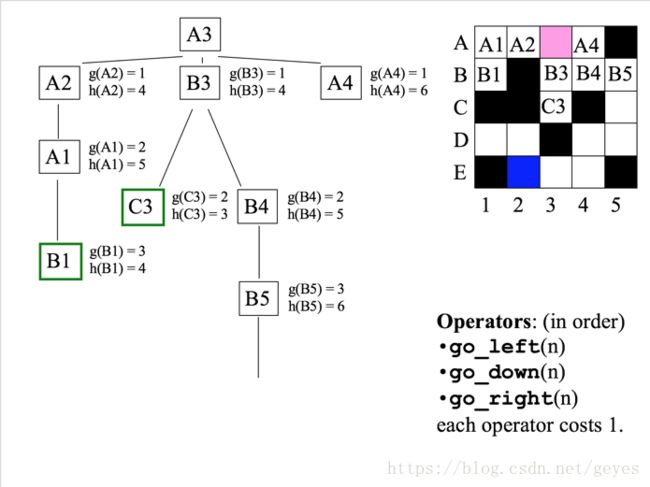
下图是一个A算法的例子:这是一个迷宫问题,初始状态是粉色的点,目标状态是蓝色的点。将粉点移动到蓝点即可。图中的树说明了用A树的搜索过程。H(n)依然使用Manhattan距离
说到这,A算法的基本概念已经介绍完毕。一下附上A算法的实现代码(Python)。以解决8-puzzle问题作为背景。
实现代码
import numpy as np
import Queue
import copy
DEFAULT_PUZZLE = np.array([1,2,3,4,8,0,7,6,5]).reshape((3,3))
GOAL_STATE = np.array([1,2,3,4,5,6,7,8,0]).reshape((3,3))
STATE_TABLE = dict() # store the state already check
class Node():
'''
:description: define the Node class
'''
def __init__(self,puzzle,depth,total_cost,blank_index_i,blank_index_j):
self.puzzle = puzzle
self.depth = depth
self.total_cost = total_cost
self.blank_index_i = blank_index_i
self.blank_index_j = blank_index_j
def get_depth(self):
return self.depth
def get_puzzle(self):
return self.puzzle
def get_total_cost(self):
return self.total_cost
def get_blank_index_i(self):
return self.blank_index_i
def get_blank_index_j(self):
return self.blank_index_j
def __lt__(self, other):
return self.total_cost < other.total_cost
def Init_input_puzzle():
'''
:description:
Initializing the input puzzle matrix, and choose the algorithm
:input: None
:return:
puzzle: the puzzle need to solved
key: the choice of algorithm
blank_index_i : the blank block index
blank_index_j : the blank block index
'''
print "Welcome to Geyeshui's 8-Puzzle solver"
key = input("Inpute 1 to use the defualt puzzle, or 2 to enter your own puzzle: \n")
if key == 1:
puzzle = DEFAULT_PUZZLE
else:
print "Enter your puzzle use a zero to represent the blank"
puzzle_input = []
for i in range(3):
row = raw_input("Enter the "+str(i+1)+"th row, use SPACE bewtween numbers: \n")
puzzle_input = puzzle_input + [eval(i) for i in row.split()]
puzzle = np.array(puzzle_input).reshape((3,3))
print "Enter your choice of algorithm"
print "1.Uniform cost search"
print "2.A* with the Misplaced title heuristic"
key = input("3.A* with the Manhattan distance heuristic \n")
# find the blank index
for i in range(3):
for j in range(3):
if puzzle[i][j]==0:
blank_index_i = i
blank_index_j = j
return puzzle, key, blank_index_i, blank_index_j
def Get_heuristic_cost(key,puzzle):
'''
:description:
according the algorithm you choice return the corresponding h(n) value
:inpute:
key : the algorithm index number
puzzle : the puzzle needed to estimate the h(n)
:return:
h_n : the h(n) value
'''
h_n = 0
if key == 1:
h_n=0
elif key ==2:
for i in range(3): # calculate the misplace number, excluding the blank.
for j in range(3):
if puzzle[(i,j)] != GOAL_STATE[(i,j)]:
if i==2 and j==2:
continue
else:
h_n = h_n+1
else:
for i in range(3): # calculate the manhattan distance
for j in range(3):
num = puzzle[(i,j)]
if num==0:
continue
else:
index_num_i = (num-1)/3
index_num_j = (num-1)%3
h_n = h_n + (abs(i-index_num_i)+abs(j-index_num_j))
return h_n
def Is_goal_state(puzzle):
'''
:description: return Ture if the puzzle is the goal state, False otherwise
:input:
puzzle: the puzzle needs to be check
:return:
Ture: if puzzle is the goal state
False: if it is not
'''
if sum(sum(puzzle==GOAL_STATE))==9:
return True
else:
return False
def Move_up(puzzle,index_i,index_j):
'''
:description:
move up the blank block if it can.
:param
puzzle: the puzzle which needs the operation
:return:
puzzle: puzzle after move up
True: if it can move up
False: if it is illegal to move up
'''
if index_i>0:
puzzle[index_i-1][index_j],puzzle[index_i][index_j] \
= puzzle[index_i][index_j],puzzle[index_i-1][index_j]
if STATE_TABLE.get(str(puzzle),0) == 1:
return None,False
else:
STATE_TABLE[str(puzzle)] = 1
return puzzle,True
else:
return None,False
def Move_down(puzzle,index_i,index_j):
'''
:description:
move down the blank block if it can.
:param
puzzle: the puzzle which needs the operation
:return:
puzzle: puzzle after move down
True: if it can move down
False: if it is illegal to move down
'''
if index_i<2:
puzzle[index_i+1][index_j],puzzle[index_i][index_j] \
= puzzle[index_i][index_j],puzzle[index_i+1][index_j]
if STATE_TABLE.get(str(puzzle),0) == 1:
return None,False
else:
STATE_TABLE[str(puzzle)] = 1
return puzzle,True
else:
return None,False
def Move_left(puzzle,index_i,index_j):
'''
:description:
move left the blank block if it can.
:param
puzzle: the puzzle which needs the operation
:return:
puzzle: puzzle after move left
True: if it can move left
False: if it is illegal to move left
'''
if index_j>0:
puzzle[index_i][index_j-1],puzzle[index_i][index_j] \
= puzzle[index_i][index_j],puzzle[index_i][index_j-1]
if STATE_TABLE.get(str(puzzle),0) == 1:
return None,False
else:
STATE_TABLE[str(puzzle)] = 1
return puzzle,True
else:
return None,False
def Move_right(puzzle,index_i,index_j):
'''
:description:
move right the blank block if it can.
:param
puzzle: the puzzle which needs the operation
:return:
puzzle: puzzle after move right
True: if it can move right
False: if it is illegal to move right
'''
if index_j<2:
puzzle[index_i][index_j+1],puzzle[index_i][index_j] \
= puzzle[index_i][index_j],puzzle[index_i][index_j+1]
if STATE_TABLE.get(str(puzzle),0) == 1:
return None,False
else:
STATE_TABLE[str(puzzle)] = 1
return puzzle,True
else:
return None,False
if __name__ == '__main__':
ans = None
# key is the choice index of algorithm
puzzle, key, blank_index_i, blank_index_j= Init_input_puzzle()
STATE_TABLE[str(puzzle)] = 1
global_step = 0 # store the how many iteration we run
size_of_pq = 0 # store the max size of priority_queue
pq = Queue.PriorityQueue()
pq.put(Node(puzzle,0,Get_heuristic_cost(key,puzzle),blank_index_i,blank_index_j))
while not pq.empty():
size_of_pq = max(size_of_pq,pq.qsize())
node = pq.get()
global_step = global_step + 1
print node.get_puzzle()
if Is_goal_state(node.get_puzzle()):
ans = node
break
else:
blank_index_i = node.get_blank_index_i()
blank_index_j = node.get_blank_index_j()
up_puzzle, up_flag = Move_up(copy.deepcopy(node.get_puzzle()),blank_index_i,blank_index_j)
down_puzzle, down_flag = Move_down(copy.deepcopy(node.get_puzzle()),blank_index_i,blank_index_j)
right_puzzle, right_flag = Move_right(copy.deepcopy(node.get_puzzle()),blank_index_i,blank_index_j)
left_puzzle, left_flag = Move_left(copy.deepcopy(node.get_puzzle()),blank_index_i,blank_index_j)
if up_flag==True:
pq.put(Node(up_puzzle,node.get_depth()+1,node.get_depth()+1+Get_heuristic_cost(key,up_puzzle),
blank_index_i-1,blank_index_j))
if down_flag==True:
pq.put(Node(down_puzzle,node.get_depth()+1,node.get_depth()+1+Get_heuristic_cost(key,down_puzzle),
blank_index_i+1,blank_index_j))
if right_flag==True:
pq.put(Node(right_puzzle,node.get_depth()+1,node.get_depth()+1+Get_heuristic_cost(key,right_puzzle),
blank_index_i,blank_index_j+1))
if left_flag==True:
pq.put(Node(left_puzzle,node.get_depth()+1,node.get_depth()+1+Get_heuristic_cost(key,left_puzzle),
blank_index_i,blank_index_j-1))
print ans.get_puzzle(),ans.get_depth(),global_step,size_of_pq
以上就是A* Search Algorithm, 有什么说的不对的地方欢迎指正