R语言 logistic regression model预测泰坦尼克号生还情况
昨天data mining的作业是使用logistics regression model和SVM model预测泰坦尼克号生还情况。设计到了logistics regression model,SVM model, confusion matrix的画法,ROC curve and AUC。
实验数据
数据网址:http://biostat.mc.vanderbilt.edu/wiki/Main/DataSets
下载其中的 titanic3.csv 作为实验数据。
数据的属性如下
pclass:Passenger Class (1 = 1st; 2 = 2nd; 3 = 3rd)
survived:Survival (0 = No; 1 = Yes)
name:Name
sex:Sexage
Agesibsp:Number of Siblings/Spouses Aboard
parch:Number of Parents/Children Aboard
ticket:Ticket Number
fare:Passenger Fare
cabin:Cabin
embarked:Port of Embarkation(C = Cherbourg; Q = Queenstown; S = Southampton)
boat:Lifeboat
body:Body
Identification:Number
home.dest:Home/Destination
读入数据
在读入前我们需要注意到数据集里有很多的缺失值,这些缺失值有两种情况:NA 和 空值,其中空值相当于c(“”),为了后期处理方便,我们在读入的时候将缺失值全部用NA替代。
titanic = read.csv("C:/Users/Administrator/Desktop/titanic3.csv",head = T,na.strings=c(""));读入以后,我们将数据集分割为80%的training set 和%20 的test set。为了确保每次分割都相同,我们需要设置seed为1(set.seed(1))。
set.seed(1);
training = titanic[sort(sample(nrow(titanic),0.8*nrow(titanic),replace=F)),];
set.seed(1);
test = titanic[-sample(nrow(titanic),0.8*nrow(titanic),replace=F),];数据清洗
由于我们作业的要求是清洗在分割之后,所以需要进行两个dataset的清洗。但是建议清洗过程在读入数据后即可进行,这样就只需要清洗一个dataset。
正如前面所说,数据集里有很多的缺失值,我们的数据清洗过程就是对这些缺失值进行处理。首先我们查阅下两个dataset有多少缺失值。
sapply(training,function(x) sum(is.na(x)));结果如下
pclass:0
survived:0
name:0
sex:0
age:217
sibsp:0
parch:0
ticket:0
fare:1
cabin:809
embarked:2
boat:662
body:945
home.dest:447对test dataset进行相同的操作,我们得到了两个数据集的缺失值统计。这时候需要特别注意的是很多的属性对我们的预测是没有帮助的,如home.det并不会影响到survived,所以我们需要从原始数据集中选择与survived相关的属性。之后我们对缺失值进行处理,age的缺失值用这一列的平均值替代,fare和embarked缺失值只有三行直接删除即可。处理过程如下。
trainingdata = subset(training,select=c(1,2,4,5,6,7,9,11));
testdata = subset(test,select=c(1,2,4,5,6,7,9,11));
trainingdata$age[is.na(trainingdata$age)] = mean(trainingdata$age,na.rm=T);
testdata$age[is.na(testdata$age)] = mean(testdata$age,na.rm=T);
trainingdata = trainingdata[!is.na(trainingdata$fare),];
trainingdata = trainingdata[!is.na(trainingdata$embarked),];logistic regression model
对training数据集进行训练获得logistics regression model
logisticmodel = glm(survived ~.,family=binomial(link='logit'),data=trainingdata)
summary(logisticmodel)summary的结果如下
Call:
glm(formula = survived ~ ., family = binomial(link = "logit"),
data = trainingdata)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4734 -0.6737 -0.4454 0.6621 2.5469
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.2779888 0.5242630 10.067 < 2e-16 ***
pclass -0.9825518 0.1327505 -7.401 1.35e-13 ***
sexmale -2.5865274 0.1805126 -14.329 < 2e-16 ***
age -0.0417329 0.0072193 -5.781 7.44e-09 ***
sibsp -0.2923644 0.1022361 -2.860 0.004240 **
parch -0.1065285 0.1028224 -1.036 0.300182
fare 0.0004468 0.0020972 0.213 0.831278
embarkedQ -0.6288323 0.3341619 -1.882 0.059861 .
embarkedS -0.7634335 0.2103097 -3.630 0.000283 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1385.86 on 1043 degrees of freedom
Residual deviance: 961.26 on 1035 degrees of freedom
AIC: 979.26
Number of Fisher Scoring iterations: 5现在,我们可以分析这个拟合的模型,阅读一下它的结果。首先,我们可以看到SibSp,Fare和Embarked并不是重要的变量。对于那些比较重要的变量,sex的p值最低,这说明sex与乘客的生存几率的关系是最强的。
评估模型预测能力
对test数据集进行预测,并计算准确度,在预测是需要设置type = ‘response’,
Fittedresults = predict(logisticmodel,newdata = subset(testdata,select=c(1,3,4,5,6,7,8)),type='response');
fittedresults = ifelse(fittedresults>0.5,1,0);
Error = mean(fittedresults != testdata$survived);
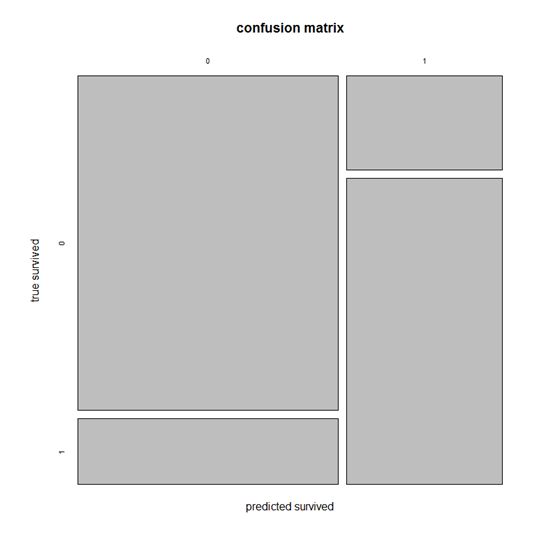
print(paste('Accuracy',1-Error));绘制混淆矩阵confusion matrix
通过table生成混淆矩阵,并绘制
ct = table((fittedresults),testdata$survived);
plot(ct, main = "confusion matrix", xlab = "predicted survived", ylab = "true survived");绘制ROC curve,计算AUC值
plot ROC curve
Library(ROCR)
p = predict(logisticmodel,newdata = subset(testdata,select=c(1,3,4,5,6,7,8)),type='response')
pr = prediction(p, testdata$survived)
prf = performance(pr, measure = "tpr", x.measure = "fpr")
plot(prf)compute AUC
auc <- performance(pr, measure = "auc")
auc <- [email protected][[1]]
print(auc)