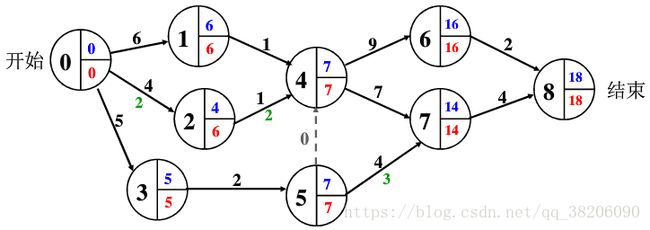
AOE网络和关键路径

更加具体的知识点请取中国大学MOOC搜索浙大版数据结构，这里只给出了代码的实现。这个算法我没有找到比较好的实现，所以自己实现的有些复杂，欢迎大家拍砖。

#include
#define INF 99999999
using namespace std;
/*
    AOE：
        在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，一个工程常被分为多个
        小的子工程，这些子工程被称为活动（Activity)，在带权有向图中若以顶点表示事件，有向边表示
        活动，边上的权值表示该活动持续的时间，这样的图简称为AOE（Activity On Edge Network）网。
        在这里边权值代表某个小组进行的时间，也就是说小组是用边来表示。结点表示某任务的开始情况。 

    关键路径：
        从起点到终点的边权之和最大的路径。这个路径可能有多条，其实我们需要的是关键路径的边权之和。
        至于哪些结点是关键结点，在下面问题的求解上可以求出来。 

    机动路径：
        在AOE网络中，若某结点工作，则它的所有前驱结点都必须被完成。也就是说它的开始时间决定于从起点到达它的路
        径中最长的那条的时间，这个时间被称作最早开始时间（earliest）。反过来，从终点向后退，如果到达结点有多条
        路径，取最小的开始时间，这个时间被称作最晚开始时间（latest）。latest - earlist大于0的结点是机动结点。
        又由于它所有的前驱结点都必须被完成，所以前进路径是一定是拓扑排序路径，后退路径一定是逆拓扑排序路径。 

    函数说明：
        mGraphRecord()和lGraphRecord()这个函数只能求出来某种情况下的机动路径和关键路径，不能求出来可能的机动路径。
        比如有三个结点：a, b, c。有以下两种路径：        1)a ---40---> c 2)a ---10---> b ---20---> c。
        这时候10若为机动路径，且机动时间为10，20则是关键路径。20若为机动路径，且机动时间为10，a则是关键路径。
        当然还可以有其他组合。这时10、20都是可能为机动路径，但是在某种求解算法下，10、20是否为机动路径是一定的。 

*/
typedef class Help
{
    public:
        int earliest, latest;
        Help(){ earliest = latest = 0; }
} *Record;
class MGraph                //矩阵图 
{
    public:
        int n;
        int **matrix;
        MGraph(){ matrix = NULL; }
};
class Node              //链式图 
{
    public:
        int n;
        int ew;
        Node(int tn, int tw){ n = tn; ew = tw; }
};
class LGraph
{
    public:
        vector *vs;
        int n;
        LGraph(){ vs = NULL; }
};
MGraph* create_mGraph()
{
    int i, from, to, w, vn, en;     //点数、边数、边权 
    MGraph *g = new MGraph();
    scanf("%d%d", &vn, &en);
    g->n = vn;
    g->matrix = new int*[vn];
    for(i = 0; i < vn; i++)
    {
        g->matrix[i] = new int[vn];
        fill(g->matrix[i], g->matrix[i] + vn, INF);
        g->matrix[i][i] = 0; 
    }
    for(i = 0; i < en; i++)
    {
        cin >> from >> to >> w;
        g->matrix[from][to] = w;    //必须是有向图 
    }
    return g;
}
LGraph *create_lGraph()
{
    int i, from, to, w, vn, en;     //点数、边数、边权 
    LGraph *g = new LGraph();
    scanf("%d%d", &vn, &en);
    g->n = vn;
    g->vs = new vector[vn];
    for(i = 0; i < en; i++)
    {
        cin >> from >> to >> w;
        Node *temp = new Node(to, w);
        g->vs[from].push_back(*temp);   //必须是有向图 
    }
    return g;
}

Record mGraphRecord(MGraph *g)
{
    int  n = g->n, countt = 0, i, j, cnt = 0;
    Record record = new Help[n];
    int *arr = new int[n], *inDegree = new int[n], *topOrder = new int[n];
    memset(inDegree, 0, n*sizeof(int));
    for(i = 0; i < n; i++)
        for(j = 0; j < n; j++)      //O(V方)
            if(g->matrix[i][j] != INF && i != j)
                inDegree[j]++;
    for(i = 0; i < n; i++)      //入度为0的进容器 
        if(inDegree[i] == 0)
            arr[countt++] = i;
    while(countt != 0)      //O(V方) 
    {
        int out = arr[--countt];    //出容器时记录序列
        topOrder[cnt++] = out;
        for(i = 0; i < n; i++)
            if(g->matrix[out][i] != INF && out != j && --inDegree[i] == 0)      //删除相应的边
            {
                arr[countt++] = i;      //入度为0的进容器
                if(record[i].earliest < record[out].earliest + g->matrix[out][i])   //顺序求最早开始时间 
                    record[i].earliest = record[out].earliest + g->matrix[out][i];  
            }
    }
    for(i = 0; i < n; i++)      //有相同earliest的补上边权 0 
        for(j = 0; j < n && i != j; j++)
            if(record[i].earliest == record[j].earliest)
                g->matrix[i][j] = 0;
    if(cnt != n)
    {
        cout << "图有环！\n";
        return NULL;
    }
    for(i = 0; i < n; i++)      
        record[i].latest = record[n - 1].earliest;
    while(cnt)          //O(V方) 
    {
        int rev = topOrder[--cnt];
        for(j = 0; j < n; j++)
            if(g->matrix[j][rev] != INF && j != rev)        //逆序求最晚开始时间 
                if(record[j].latest > record[rev].earliest - g->matrix[j][rev])
                    record[j].latest = record[rev].earliest - g->matrix[j][rev];
    }
    return record;
}

Record lGraphRecord(LGraph *g)
{
    int n = g->n, countt = 0, i, j, cnt = 0;
    int *arr = new int[n], *inDegree = new int[n], *topOrder = new int[n];
    Record record = new Help[n];
    memset(inDegree, 0, n * sizeof(int));
    for(i = 0; i < n; i++)      //O(E)
        for(j = 0; j < g->vs[i].size(); j++)
            inDegree[g->vs[i][j].n]++;
    for(i = 0; i < n; i++)          //入度为0的进容器 
        if(inDegree[i] == 0)
            arr[countt++] = i;
    while(countt != 0)
    {
        int out = arr[--countt];        //出容器时记录序列 
        topOrder[cnt++] = out;  
        for(j = 0; j < g->vs[out].size(); j++)
        {
            i = g->vs[out][j].n;
            if(--inDegree[i] == 0)  //删除相应的边且入度为0的进容器 
            {
                arr[countt++] = i;
                if(record[i].earliest < record[out].earliest + g->vs[out][j].ew)    //顺序求最早开始时间 
                    record[i].earliest = record[out].earliest + g->vs[out][j].ew;
            }
        }
    }
    if(cnt != n)
    {
        cout << "图有环！\n";
        return NULL;
    }
    for(i = 0; i < n; i++)
        for(j = 0; j < n && i != j; j++)
            if(record[i].earliest == record[j].earliest)
                g->vs[i].push_back(*(new Node(j, 0)));
    for(i = 0; i < n; i++)
        record[i].latest = record[n - 1].earliest;
    while(cnt)  //O(V*E)
    {
        int rev = topOrder[--cnt];
        for(i = 0; i < n; i++)
            for(j = 0; j < g->vs[i].size(); j++)
                if(g->vs[i][j].n == rev && record[i].latest > record[rev].earliest - g->vs[i][j].ew)
                    record[i].latest = record[rev].earliest - g->vs[i][j].ew;
    }

    return record;
}

void printFlexibleEdgeM(MGraph *g, Record record)
{
    for(int i = 0; i < g->n; i++)
        for(int j = 0; j < g->n; j++)
            if(g->matrix[i][j] != INF && i != j && record[j].latest - g->matrix[i][j] > record[i].earliest)
                cout << "起点：" << i << "   终点：" << j << "   机动时间：" <<    
                    record[j].latest - g->matrix[i][j] - record[i].earliest << endl; 
}

void printFlexibleEdgeL(LGraph *g, Record record)
{
    for(int i = 0; i < g->n; i++)
        for(int j = 0; j < g->vs[i].size(); j++)
            if(g->vs[i][j].ew != 0 && record[g->vs[i][j].n].latest - g->vs[i][j].ew > record[i].earliest)
                cout << "起点：" << i << "   终点：" << g->vs[i][j].n << "   机动时间：" <<
                    record[g->vs[i][j].n].latest - g->vs[i][j].ew - record[i].earliest << endl; 
}
int main()
{
    LGraph *lg = create_lGraph();
    MGraph *mg = create_mGraph();
    Record r1 = mGraphRecord(mg);
    Record r2 = lGraphRecord(lg);
    printFlexibleEdgeM(mg, r1);
    cout << "----------------------" << endl; 
    printFlexibleEdgeL(lg, r2);
    for(int i = 0; i < mg->n; i++)
        cout << r1[i].earliest << " " << r1[i].latest << endl;
    cout << "----------------------" << endl; 
    for(int i = 0; i < lg->n; i++)
        cout << r2[i].earliest << " " << r2[i].latest << endl;
    return 0;
}

/*
    input:
        9 11 
        0 1 6
        0 2 4
        0 3 5
        1 4 1
        2 4 1
        3 5 2
        5 7 4
        4 6 9
        4 7 7
        7 8 4
        6 8 2
        9 11 
        0 1 6
        0 2 4
        0 3 5
        1 4 1
        2 4 1
        3 5 2
        5 7 4
        4 6 9
        4 7 7
        7 8 4
        6 8 2
    output:
        0 3 1 2 4
        0 3 1 2 4
*/