SPFA--------高效率的图解法

转明出处：http://lib.csdn.net/article/datastructure/10344

SPFA（Shortest Path Faster Algorithm）（队列优化）算法是求单源最短路径的一种算法，它还有一个重要的功能是判负环（在差分约束系统中会得以体现），在Bellman-ford算法的基础上加上一个队列优化，减少了冗余的松弛操作，是一种高效的最短路算法。（spfa会被恶意数据卡掉，如果没必要判负环建议使用Dijkstra）

                             

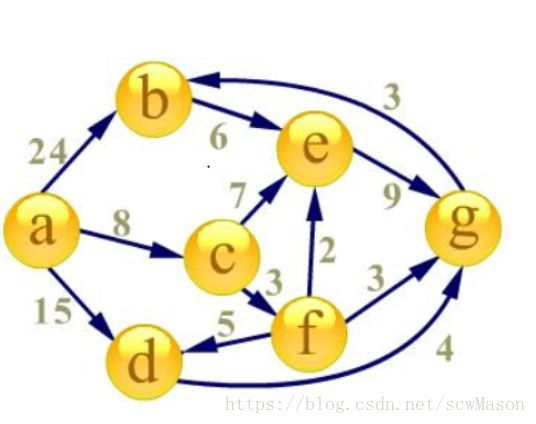
我们以上面的图为例：

首先建立起始点a到其余各点的
最短路径表格

                                  

首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

                                  

在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

                                 

在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

                                 

在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

 队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

 

 

                               

在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

                               

在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

                           

在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

 

                          

在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

                         

在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４

这这个是单源最短路算法，效率很高，和Dijkstra二分天下。时间复杂度的分析，暂时我还没做，先摘抄2009年OI国家集训队广东中山纪念中学的姜碧野学长一篇论文中的分析：

　　在一般情况，SPFA的效率很高，可以证明SPFA的期望复杂度为O(KM)，K<2。但由于证明还不够严谨且适用性不广(存在针对性数据)，在此不再赘述。但将会在随后的测试中用实际数据来验证SPFA的高效性。

　　注：上文中所说M表示图中的边数。

　　其实算法思想很简单。假设起点叫S，终点叫T。用(u,v)表示边u->v的长度。依旧用d[i]表示S->i的最短路径。我们采用“松弛操作”，不断更新可以更新的d，最终无法更新终止。算法如下：个是单源最短路算法，效率很高，和Dijkstra二分天下。时间复杂度的分析，暂时我还没做，先摘抄2009年OI国家集训队广东中山纪念中学的姜碧野学长一篇论文中的分析：

　　在一般情况，SPFA的效率很高，可以证明SPFA的期望复杂度为O(KM)，K<2。但由于证明还不够严谨且适用性不广(存在针对性数据)，在此不再赘述。但将会在随后的测试中用实际数据来验证SPFA的高效性。

　　注：上文中所说M表示图中的边数。

　　其实算法思想很简单。假设起点叫S，终点叫T。用(u,v)表示边u->v的长度。依旧用d[i]表示S->i的最短路径。我们采用“松弛操作”，不断更新可以更新的d，最终无法更新终止。算法如下：

引入问题：

      有N个城市（标号为0-N-1），M条道路（无向边）、并且给出M条道路的距离属性和花费属性。现在给定起点s和终点d，求从起点到终点的最短路径及花费。注意：如果有多条最短路径，则选择花费最大的那条，然后输出到终点最短路径的数量以及最终选择

#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 510;
const int INF = 0x3fffffff;
struct node
{
	int v;
	int dis;
	node(int a, int b) :v(a), dis(b) {}
};
vector Adj[MAXN];
int n, m, st, ed;
int d[MAXN], num[MAXN], weight[MAXN];
int sum[MAXN], w[MAXN];
set pre[MAXN];
bool inq[MAXN];
bool SPFA(int s)
{
	memset(inq, false, sizeof(inq));
	memset(num, 0, sizeof(num));
	fill(d, d + MAXN, INF);
	memset(w, 0, sizeof(w));
	queue Q;
	Q.push(s);
	inq[s] = true;
	num[s]++;
	d[s] = 0;
	w[s] = weight[s];
	while (!Q.empty())
	{
		int u = Q.front();
		Q.pop();
		inq[u] = false;
		for (int j = 0; j < Adj[u].size(); j++)
		{
			int v = Adj[u][j].v;
			int ds = Adj[u][j].dis;
			if (d[u] + ds < d[v])
			{
				d[v] = d[u] + ds;
				w[v] = w[u] + weight[v];
				num[v] = num[u];
				pre[v].clear();
				pre[v].insert(u);
				if (!inq[v])
				{
					Q.push(v);
					inq[v] = true;
					sum[v]++;
					if (sum[v] >= n)
					{
						return false;
					}
				}
			}
			else if (d[u] + ds == d[v])
			{
				if (w[v] < w[u] + weight[v])
				{
					w[v] = w[u] + weight[v];
				}
				pre[v].insert(u);
				num[v] = 0;
				set::iterator it;
				for (it = pre[v].begin(); it != pre[v].end(); it++)
				{
					num[v] += num[*it];
				}
			}
		}
	}
	return true;
}
int main()
{
	cin >> n >> m >> st >> ed;
	for (int i = 0; i < n; i++)
	{
		cin >> weight[i];
	}
	int u, v, wt;
	for (int i = 0; i < m; i++)
	{
		cin >> u >> v >> wt;
		Adj[u].push_back(node(v, wt));
		Adj[v].push_back(node(u, wt));
	}
	SPFA(st);
	cout << num[ed] << endl;
	cout << w[ed];
	system("pause");
	return 0;
}