基于Pandas实现皮尔逊相关与余弦相似度在工业大数据分析中的应用实践
大数据时代,工业、工程专业理论贯穿于大数据分析的方方面面。很多原有的认知将被颠覆,很多原有的制度将面临挑战。所以大数据的出现改变了很多人的思维方式,更多的人拥抱大数据。
1. 相关关系
相关关系是客观现象存在的一种非确定的相互依存关系,即自变量的每一个取值,因变量由于受随机因素影响,与其所对应的数值是非确定性的。相关分析中的自变量和因变量没有严格的区别,可以互换。
事物或现象的相关种类可以从方向、形态及变量个数诸多方面划分。
1、正相关、负相关和零相关
正相关是指两列变量变动方向相同,一列变量由大到小或由小到大变化时,另一列变量亦由大到小或由小到大变化,相关系数在0.00与1.00之间。如身高与体重,身高越长,体重就越重。
负相关是指两列变量变动方向相反,一列变量由大到小或由小到大变化时,另一列变量反而由小到大或由大到小变化,相关系数在-1.00与0.00之间。例如随着计算练习次数增加或练习时间加长,计算错误就越少等等。
零相关是指两列变量之间没有关系,即一列变量变动时,另一列变量作无规律的变动,又称为不相关,相关系数为0。如相貌与人的行为等现象之间的关系,都属于零相关。

2、直线相关和曲线相关
直线相关是指两列变量中的一列变量在增加(或减少)时,而另一列变量随之而增加(或减少),或这一列变量在增加时,而另一列变量则相应地减少。它们之间存在一种直线关系,或线性相关。直线相关可用直线拟合。
非线性相关(曲线相关)是指两列伴随相变化的变量,未能形成直线关系。曲线相关有很多种,不能用曲线拟合。

3、完全相关、强相关和弱相关
完全相关是指两列变量的关系是一一对应,完全确立的关系。在坐标轴上描绘两列变量时会形成一条直线。
强相关又称高度相关,即当一列变量变化时,与之相应的另一列变量增大(或减少)的可能性非常大。在坐标图上则表现为散点图较为集中在某条直线的周围,相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强。
弱相关又称低度相关,即当一列变量变化时,与之相对应的另一列变量增大(或减少)的可能性较小。亦即两列变量之间虽然有一定的联系,但联系的紧密程度较低,相关系数越接近于0,相关度越弱。在坐标涂上表现出散点比较分散地分布在某条直线的周围。
通常情况下通过以下取值范围判断变量的相关强度:
| 相关系数 | 相关度 |
|---|---|
| 0.8-1.0 | 极强相关 |
| 0.6-0.8 | 强相关 |
| 0.4-0.6 | 中等程度相关 |
| 0.2-0.4 | 弱相关 |
| 0.0-0.2 | 极弱相关或无相关 |
2. 大数据相关分析
大数据始于数据相关分析,相关分析探讨数据之间是否具有统计学上的关联性。这种关系既包括两个数据之间的单一相关关系,如年龄与个人领域空间之间的关系,也包括多个数据之间的多重相关关系——如年龄、体育运动爱好、个人领域空间之间的关系;既包括A与B的线性相关关系,也可以是复杂相关关系;既可以是A、B变量同时增大这种正相关关系,也可以是A变量增大时B变量减小这种负相关,还包括两变量共同变化的紧密程度——即相关系数。
其中,对于因果关系是相关关系唯一不研究的数据关系,就是数据协同变化的内在根据。
目前分析数据相关性的方法,有两大类别,一类是基于决策树的随机森林分析相关性的方法。这一种方法的相关性判定依据是信息熵和GINI系数递减率以及数据特征在隐藏节点上出现的次数。另一类是计算相关系数方法,最具代表性的是皮尔逊相关性系数。
信息熵衡量信息的确定程度往往基于广义线性模型指数分布族中的多项分布给定概率,以二项分布为例,二项分布的中心极限定理趋近的正态分布方差就是Gini系数。因此其根本判定标准是随机变量的分布极限方差的大小,也就是数据分类对于该特征的离散程度。
而皮尔逊相关性系数,不仅包含了这种离散程度,还直接建立起特征与结果之间线性联系的评价标准,即协方差标准。在数据量级较大,噪声不明显时,二者会相对接近,但数据不足,噪声较大时,随机森林便不稳定,皮尔逊相关性系数就会优于随机森林评价。
皮尔逊相关系数为了确定 每个特征之间是否紧密相关,如果很相关就属于重复特征,可以去除。 我们输入机器学习模型中的每个特征都独一无二,这才是最佳。
2.1. 皮尔逊相关系数
皮尔逊相关系数( Pearson correlation coefficient),是用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。
ρ X , Y = c o v ( X , Y ) σ X σ Y \rho_{X,Y}=\frac{cov(X,Y)}{\sigma _{X}\sigma_{Y}} ρX,Y=σXσYcov(X,Y)
-
协方差(Covariance)
协方差是一个反映两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值,反之相反,公式如下:
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) n − 1 cov(X,Y)=\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{n-1} cov(X,Y)=n−1∑i=1n(Xi−X)(Yi−Y) -
标准差:
σ X = 1 n − 1 ∑ i = 1 n ( X − X ‾ ) 2 \sigma_{X} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X-\overline{X})^{2}} σX=n−11i=1∑n(X−X)2
σ Y = 1 n − 1 ∑ i = 1 n ( Y − Y ‾ ) 2 \sigma_{Y} = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(Y-\overline{Y})^{2}} σY=n−11i=1∑n(Y−Y)2 -
皮尔逊相关系数推导公式
ρ X , Y = c o v ( X , Y ) σ X σ Y \rho_{X,Y}=\frac{cov(X,Y)}{\sigma _{X}\sigma_{Y}} ρX,Y=σXσYcov(X,Y)
ρ X , Y = ∑ i = 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) ∑ i = 1 n ( X − X ‾ ) 2 ∑ i = 1 n ( Y − Y ‾ ) 2 \rho_{X,Y}=\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\sum_{i=1}^{n}(X-\overline{X})^{2}}\sqrt{\sum_{i=1}^{n}(Y-\overline{Y})^{2}}} ρX,Y=∑i=1n(X−X)2∑i=1n(Y−Y)2∑i=1n(Xi−X)(Yi−Y)
-
约束条件
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)两个变量之间有线性关系
(2)变量是连续变量
(3)变量均符合正态分布,且二元分布也符合正态分布
(4)两个变量的观测值是成对的,两变量独立 -
皮尔逊相关系数的一些误区:
- 相关系数很大,但是图像不是线性相关;
- 非线性相关也会导致线性相关系数很大,如图1;
- 离群点对相关系数的影响很大,例如图2,去掉离群点后,相关系数为0.98;
- 如果两个变量的相关系数很大也不能说明两者相关,例如图3,可能是受到了异常值的影响。
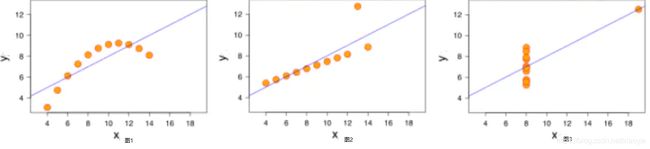
- 离群点
在样本空间中,与其他样本点的一般行为或特征不一致的点,我们称为离群点。
相关性理论优选方案:
判定相关是否密切时,要把样本量大小与相关系数取值大小综合起来考虑。如果样本量较小时,受取样偶然因素的影响较大,很可能本来无关的两类事物,却计算出较大的相关系数,一般要经过统计检验方能确定变量之间是否存在显著的相关。另外,若是非线性相关关系,而用直线相关计算r值可能很小,但不能说两变量关系不密切。
2.2 余弦相似度
余弦相似度,也称为余弦距离,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,夹角等于0,即两个向量相等,这就叫"余弦相似性"。
余弦取值范围为[-1,1]。求得两个向量的夹角,并得出夹角对应的余弦值,此余弦值就可以用来表征这两个向量的相似性。夹角越小,趋近于0度,余弦值越接近于1,它们的方向更加吻合,则越相似。当两个向量的方向完全相反夹角余弦取最小值-1。当余弦值为0时,两向量正交,夹角为90度。因此可以看出,余弦相似度与向量的幅值无关,只与向量的方向相关。
由于连续离散点连线的斜率存在无穷大的问题,所以,把角度和斜率转换为向量夹角余弦值,方便比较相似度。
c ( A , B ) = A . B ∣ A ∣ ∣ B ∣ = ∑ i = 1 n A i B i ∑ i = 1 n ( A i ) 2 ∑ i = 1 n ( B i 2 ) c(A,B)=\frac{A.B}{\left | A \right |\left | B \right |}=\frac{\sum_{i=1}^{n}A_{i}B_{i}}{\sqrt{\sum_{i=1}^{n}(A_{i})^{2}}\sqrt{\sum_{i=1}^{n}(B_{i}^{2})}} c(A,B)=∣A∣∣B∣A.B=∑i=1n(Ai)2∑i=1n(Bi2)∑i=1nAiBi
这里的 A i A_{i} Ai、 B i B_{i} Bi分别代表向量A和B的各分量。
皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进,理论推导公式网上有可查。
2.3. 图形分析方法与散点图
相关散点图(correlation scatter diagram)。是统计分析图的一种。指用于观察两个变量的相关模式的散点图。以圆点的多少、疏密表示两变量问关系的程度。两个变量的相关模式和强弱可以在相关散点图上粗略地看出。若散点呈倾斜的椭圆形,则说明两个变量有线性相关。散点越密集且椭圆形越窄长,则相关程度越高;若散点呈曲线状(如弯月形),则说明两个变量是曲线相关。绘制相关散点图是相关分析的步骤之一。
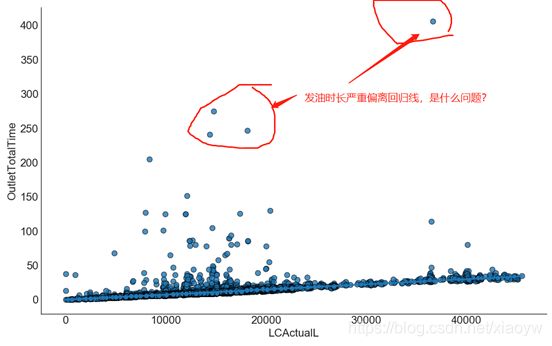
散点图是确定变量之间是否存在相关关系及关系紧密程度的简单而又直观的方法。如果所有散点分布呈椭圆状,则说明二变量之间呈线性关系。如果散点图呈现圆形,就为零相关或弱相关。散点图可以做出一个拟合直线,代表数据点的相关趋势。这条直线是用统计方法求得的,因每个数据点与它的离差最小,所以称为最佳拟合直线。数据与最佳拟合直线之间的离差越小,拟合直线对数据相关关系预测的可靠度即精确度会越高。用一些合理的统计指标对相关现象的观测值进行的统计分析叫相关分析。
另外,上图中严重偏离线性回归线的点,需要重点关注的离群点,需要进一步删除或其他处理。
2.4. 卡方检验
分析定类数据与定类数据的关系,可以使用卡方检验,独立性检验(卡方检验)就是用于研究定类数据和定类数据之间的关系情况,比如,研究不同药物的疗效是否有差异,若疗效因药物种类不同而产生差异,则表明两种药物的疗效不相同,也即说明药物和疗效之间存在关联。反之,若不同种类的药物疗效相同,则说明药物和疗效是相互独立的。
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。(更多参考:卡方检验、卡方分布)
Logistic回归分析的结果和卡方检验的结果不一样?
这种情况是正常的,是由于分别使用单因素分析和多因素分析造成的。卡方检验相对于Logistic回归而言一次只能考虑一个因素,因此在卡方检验中你的性别、专业是分开做的(单因素分析)。如果在Logistic回归中你也分开做性别、专业(单因素分析),那么结果就会与卡方检验完全一样。 但是,如果你在Logistic回归中同时使用性别、专业等多个因素(多因素分析),那么模型中的各个因素是可以产生相互影响的,有可能产生共线性。如果性别、专业存在共线性的话,那么Logistic逐步回归就会自动放弃其中一个模型影响力较小的因素(即使这个因素在单因素分析中有显著性也会被放弃)以防止共线性的产生。
元素/特征/属性的异常值的选择情况,可以使用直方图、箱型图、Z分数法等筛选。如 Python 探索性数据分析(Exploratory Data Analysis,EDA) ,数据探索的同时,也可以排除单个变量的异常值。而对于离散属性(或离散化)的分类,可以使用 等距分类、等频分类 等,但是这样分类不能体现出与其他属性或结果的相关性。
3. 大数据相关分析的应用
获得相关系数有什么用呢?简而言之,有了相关系数,就可以根据回归方程,进行A变量到B变量的估算,这就是所谓的回归分析,因此,相关分析是一种完整的统计研究方法,它贯穿于提出假设,数据研究,数据分析,数据研究的始终。
3.1. 皮尔逊相关与热力图
以特殊高亮的形式显示相关系数的图示,高亮一般为正相关越强,高度深色表示为负相关越强。

获取相关系数如下:

参考代码:
import pymongo
import numpy as np
from datetime import datetime
import pandas as pd
import matplotlib.pyplot as plt
names = ['Total','CraneP','SpeciL','LCActL','Effi','Time','Month','Day','LossL','T','Density']
def get_DataFromExcel():
df = pd.read_excel('e:/data1.xlsx')
#转换Object类型为可计算类型
df['OutletTotalTime'] = df['OutletTotalTime'].astype('int64')
df['CraneP'] = df['CraneP'].astype('int64')
df['SpecifiedL'] = df['SpecifiedL'].astype('float64')
df['LCActualL'] = df['LCActualL'].astype('float64')
df['Month'] = df['Month'].astype('int64')
df['Time'] = df['Time'].astype('int64')
df['Day'] = df['Day'].astype('int64')
#df0['Effi'] = df0['Effi'].astype('float64')
return df
# 相关系数热力图
def draw_corr(df,to_xlsx):
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
#相关系数矩阵图(Correlation Matrix Plot)
correlations = df.corr(method='pearson',min_periods=1) #计算变量之间的相关系数矩阵
correlations.to_excel(to_xlsx)
print(correlations)
# plot correlation matrix
fig = plt.figure() #调用figure创建一个绘图对象
ax = fig.add_subplot(111)
cax = ax.matshow(correlations,cmap = 'inferno', vmin=-1, vmax=1) #绘制热力图,从-1到1
fig.colorbar(cax) #将matshow生成热力图设置为颜色渐变条
ticks = np.arange(0,11,1) #生成0-9,步长为1
ax.set_xticks(ticks) #生成刻度
ax.set_yticks(ticks)
ax.set_xticklabels(names) #生成x轴标签
ax.set_yticklabels(names)
plt.show()
df0 = get_DataFromExcel()
draw_corr(df1,to_xlsx='e:/dcorr1.xlsx')
3.2. 散点图分析
DataFrame用plotting的scatter_matrix创建散布图矩阵,并且支持对角线上放置各变量的直方图或密度图(diagonal=‘kde’)。

参考代码:
import pymongo
import numpy as np
from datetime import datetime
import pandas as pd
import matplotlib.pyplot as plt
names = ['Total','CraneP','SpeciL','LCActL','Effi','Time','Month','Day','LossL','T','Density']
def get_DataFromExcel():
df = pd.read_excel('e:/data1.xlsx')
#转换Object类型为可计算类型
df['OutletTotalTime'] = df['OutletTotalTime'].astype('int64')
df['CraneP'] = df['CraneP'].astype('int64')
df['SpecifiedL'] = df['SpecifiedL'].astype('float64')
df['LCActualL'] = df['LCActualL'].astype('float64')
df['Month'] = df['Month'].astype('int64')
df['Time'] = df['Time'].astype('int64')
df['Day'] = df['Day'].astype('int64')
#df0['Effi'] = df0['Effi'].astype('float64')
return df
def draw_scatter_matrix(df):
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
#散布图矩阵(Scatterplot Matrix)散点图
pd.plotting.scatter_matrix(df,figsize=(10,10),diagonal='kde')
plt.show()
df0 = get_DataFromExcel()
draw_scatter_matrix(df=df1[['LCActualL','OutletTotalTime','OilTemperature','OilDensity']])
大数据相关分析是大数据人工智能工作开始,后续将开展数据分析、挖掘、趋势分析,欢迎读者反馈。
参考:
《[数学建模第五讲] 皮尔逊相关系数》 简书,茶酒qqq 2020.02
《用Python统计推断——相关性篇》 知乎 , 梁巨摇 2019.01
《如何理解皮尔逊相关系数(Pearson Correlation Coefficient)?》 知乎 微调 2018.04
《Python 卡方检验》 CSDN博客 ,薛定谔的DBA 2018.01
《Python科学计算初探——余弦相似度》 CSDN博客, 肖永威 2018.04