直方图均衡（Histogram Equalization）

官网教程

直方图均衡的原理

1. 原理参考 ，或者数字图像处理p72
2. 将图像像素值概率分别拉升，扩大分别范围，提高对比度，应用于背景和前景像素差别不大

最终的映射公式：$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{P}_r(r_j)=\frac{L-1}{MN}\sum _{j=0}^k{n}_{j}k=1,2,3...L-1$$

$s_k$：目标像素值
$r_k$：原始像素值
$L$：灰度级（8位256）
$P_r(r_j)$：$r_j$在原始图中的概率
$MN$：图像的像素总数cols×rows
$n_j$：原始图像中，像素值为 j 的个数

---

代码

1. 直方图均衡 （参见官网）

2. 直方图的计算(官网代码教程)

#include 
#include 

using namespace cv;
using namespace std;


int main(void)
{
    Mat src = imread("../res/beauty.jpg");
    if(src.empty())
    {
	cout << "can't load the image" << endl;
    }

    vector<Mat> bgr_plances;
    cv::split(src,bgr_plances); //将src每个通道分开，分别存到bgr_plances
	
    int histSize=256; //bins
    float range[]= {0,256};     
    const float* histRange = {range};

    bool uniform = true, accumulate = false;

    Mat b_hist, g_hist, r_hist;
    cv::calcHist(&bgr_plances[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRange, uniform, accumulate);
    cv::calcHist(&bgr_plances[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRange, uniform, accumulate);
    cv::calcHist(&bgr_plances[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRange, uniform, accumulate);

    

    int hist_w = 512, hist_h = 400;  //定义直方图的长宽
    int bin_w = cvRound((double)hist_w/histSize);  //将宽为512的图分成 histSize等分，每份相当于一个bin

    Mat hist_Image(hist_h,hist_w,CV_8UC3,Scalar(0,0,0)); //创建直方图，下面会在上面画图

//范围规范化，因为像素值个数大小不一,像素0的可能1000个，像素255可能10，所以将他们规范到 0-hist_Image.rows之间，满足图像高度，没有溢出
    normalize(b_hist,b_hist,0,hist_Image.rows,NORM_MINMAX,-1,Mat());
    normalize(g_hist,g_hist,0,hist_Image.rows,NORM_MINMAX,-1,Mat());
    normalize(r_hist,r_hist,0,hist_Image.rows,NORM_MINMAX,-1,Mat());


//开始画图
    for(int i=1;i<histSize; i++)
    {
	line(hist_Image,Point(bin_w*(i-1),hist_h-cvRound(b_hist.at<float>(i-1))), //从第0个点到第1个点
		Point(bin_w*i,hist_h-cvRound(b_hist.at<float>(i))),
		Scalar(255,0,0),2,8,0
	    );
	line(hist_Image,Point(bin_w*(i-1),hist_h-cvRound(g_hist.at<float>(i-1))),
		Point(bin_w*i,hist_h-cvRound(g_hist.at<float>(i))),
		Scalar(0,255,0),2,8,0
	    );	
	line(hist_Image,Point(bin_w*(i-1),hist_h-cvRound(r_hist.at<float>(i-1))),
		Point(bin_w*i,hist_h-cvRound(r_hist.at<float>(i))),
		Scalar(0,0,255),2,8,0
	    );
    }

    imshow("CalHist Demo", hist_Image);
    waitKey();
	return 0;
};

结果：

原图：

直方图：

---

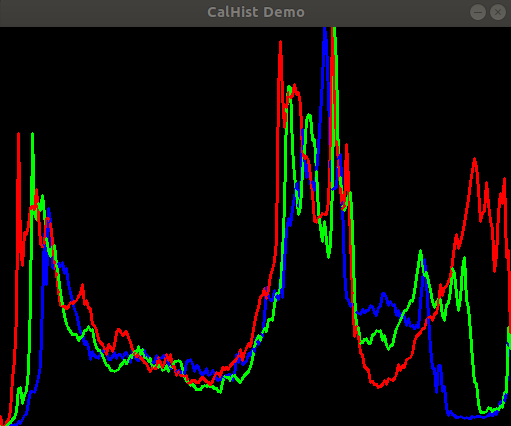
OpenCV API

1 将一副图像进行直方图均衡输出

void cv::equalizeHist
(
InputArray src,     // Source 8-bit single channel image
OutputArray dst     //Destination image of the same size and type as src
)

2 计算一组或者一个图像的直方图（参数还是比较复杂，可以参考上面的例程或者官网函数原型处也有例子）

void cv::calcHist
(
const Mat * images,    // 原图，他们都有相同的深度、尺寸，但是可以有不同的通道数
int nimages,        // 原图像的个数
const int * channels,    // 数组{[0,1],[2,3,4]} 意味着第一个图像2通道，第二张3通道；0代表就一张图像
InputArray mask,    // 掩膜，如果不为空，必须是8位和images大小一样，mask非0意味着原图此位置计算，0意味着忽略此处元素
OutputArray hist,    // 输出的直方图（ Mat对象）
int dims,        // 直方图的维数，只统计像素，那就是1
const int * histSize,    // 每个维度使用的 bins（计算像素的话就是256）, 多维度的话，传递的应该是int型数组的首地址
const float ** ranges,    // 每一个维度的bins的范围，如果下一个参数uniform=true，则只需要定义下限和上限；
              如像素值0-255，如果histSize=256,则每个bin就按1步进；
               如果不是均匀分布（uniform=false），则数组里面每个元素包含 bins+1个元素（为了定义每个bin与bin之间的界限），
bool uniform = true,    // 看上一个参数
bool accumulate = false    // 没看懂，false即可
)

3 该函数分为范围归一化与数据值归一化（参考下面链接）
cv::normalize
(
InputArry src,     // 输入数组
InputOutputArray dst,    // 输出的结果数组
double alpha=1,    // 1,用来规范值，2.规范范围，并且是下限；
double beta=0,    // 只用来规范范围并且是上限
int norm_type=NORM_L2,    // 归一化选择的数学公式类型
int dtype=-1,        // -1意味着输出数组和输入类型一样
InputArray mask=noArry()    // 掩码
)