Introduction to Optimization(一):一维最优化方法

最近经常用到scipy.optimize 想来一直把它当成黑箱实在是不舒服，所以还是决定去了解一下其中的算法，幸来看见《an Introduction to Optimization》这本书里讲了很多优化方法。便于让自己燕过流痕故这里做个笔记.仅用于个人回顾.

---

这里是正文……..

第7章: 一维搜索方法.
这里主要说一下这个

• 黄金分割方法

原来这就是以前听ACM大佬说的3分.

算法描述

对于函数: f(x) 搜索它在区间 [a,b] 内的极小值

1. 令 a0=a,b0=b
2. 选定一个值 ρ<12 进行缩小区间.
   s.t
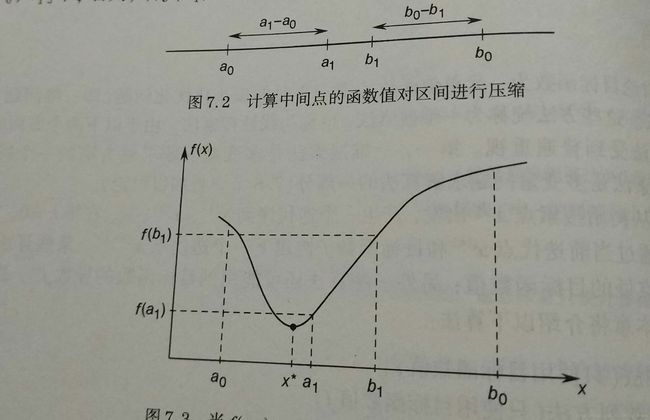
   a1−a0=b0−b1=ρ(b0−a0)
3. 计算 f(a1),f(b1)
4. 若有 f(a1)>f(b1) , 则极小值点在区间 [a1,b0] ,替换掉，反之亦然

如下图

分析

关键在于 ρ 的选取，我们希望选取 ρ 使得计算量变小，即
（假设 f(a1)<f(b1) ）当我们替换为 [a0,b1] 时，使得下一轮 b2=a1 这样下一轮就不需要计算 f(b2) 了.不失一般性设 [a0,b0] 长度为1,因此有

ρ(b1−a0)ρ(1−ρ)ρ=b1−b2=1−2ρ=3−5√2

区间按照
1−ρ=5√−12
的黄金比例压缩，所以称为黄金分割. 不难验证这个搜索方法以指数级数压缩

py代码

def golden(fun, bound, tot=1e-6):
    """
    一维黄金分割找极小值
    :param fun: 1元函数
    :param bound: [lb,ub]
    :param tot: 最小区间长度
    :return: [x0, minimal_val]
    """
    a, b = bound
    p = 0.382  # 黄金分割 1-p ~= 0.618
    a_next = None
    b_next = None
    while b-a > tot:
        if a_next is None:
            a1 = a+p*(b-a)
            f_a1 = fun(a1)
            a_next = (a1, f_a1)
        if b_next is None:
            b1 = a+(1-p) * (b-a)
            f_b1 = fun(b1)
            b_next = (b1, f_b1)
        if a_next[1] < b_next[1]:
            b = b_next[0]
            b_next = a_next
            a_next = None
        else:
            a = a_next[0]
            a_next = b_next
            b_next = None
    return [(b+a)/2, fun((b+a)/2)]

test

    fun = lambda x: x**4 - 14*x**3 + 60*x**2 - 70*x
    ret = golden(fun, [0, 2])
    from scipy.optimize import minimize_scalar
    print('my ans\n', ret)
    res = minimize_scalar(fun,bounds=[0,2],method='brent')
    print('scipy\n',res)

结果如下

可以看到scipy.optimize 迭代次数很小，因为他用的brent 方法。 这个方法，我暂时留个坑，据书中介绍用的很多.

scipy.optimize 里的minimize

关于这个去看optimize 的文档可以发现里面有一个minimize_scalar 里面实现了两个函数的一维标量搜索:

• golden
• brent

具体可见文档