Canvas 画正n角星
Canvas 画正n角星
看到canvas画图是不由得想起之前的gostscript,两者很类似,借鉴crystalhuhu 的五角星画法
先讲如何画一个正规的五角星
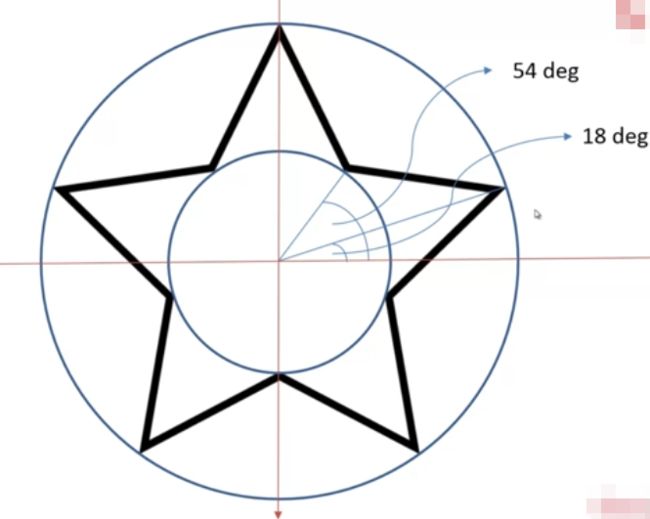
在五角星的内外画两个圆,五角星有五个角,360/5=72度
所以得出这两个角的度数
然后算出这两个点坐标
角度转弧度
角度/180*Math.PI
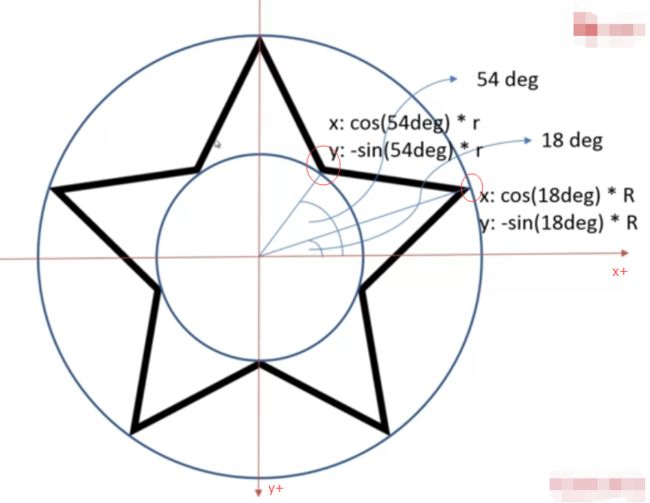
所以外顶点坐标x: Math.cos( (18+72*i)/180*Math.PI) * R
y: Math.sin((18+72*i)/180*Math.PI) * R
所以内顶点坐标 x: Math.cos( (54+72*i)/180*Math.PI) * r
y: Math.sin((54+72*i)/180*Math.PI) * r
画完五角星后我就想何不画个n角星,说画就画:
推倒下N角星的顶点坐标:
三角星 外圆内圆中对应的顶点坐标相差120度 外圆起始角30° 内圆起始角60° 30+60 = 360/3=120
四角星 外圆内圆中对应的顶点坐标相差90度 外圆起始角22.5° 内圆起始角67.5° 30+60 = 360/4=90
五角星 外圆内圆中对应的顶点坐标相差72度 外圆起始角18° 内圆起始角54° 18+54= 360/5 =72
六角星 外圆内圆中对应的顶点坐标相差60度 外圆起始角15° 内圆起始角45° 15+45= 360/6 =60
所以外定点坐标x: Math.cos(((360/n)*(1/4)+(360/n)*1)/180*Math.PI)*R
y: Math.sin(((360/n)*(1/4)+(360/n)*1)/180*Math.PI)*R
所以内定点坐标x: Math.cos(((360/n)*(3/4)+(360/n)*1)/180*Math.PI)*R
y: Math.sin(((360/n)*(3/4)+(360/n)*1)/180*Math.PI)*R
简化后就是:
外定点坐标x: Math.cos(((360/n)*(1/4)+(360/n)*1)/180*Math.PI)*R
y: Math.sin(((360/n)*(1/4)+(360/n)*1)/180*Math.PI)*R
内定点坐标x: Math.cos(((360/n)*(3/4)+(360/n)*1)/180*Math.PI)*R
y: Math.sin(((360/n)*(3/4)+(360/n)*1)/180*Math.PI)*R
那么整段代码如下(当n>=3的时候正确):
<html>
<head>
<meta charset="utf-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<title>title>
<link rel="stylesheet" href="">
head>
<body>
<canvas id="mycanvas">canvas>
<script>
var canvas = document.getElementById('mycanvas');
canvas.width=800;//设置画布的宽度
canvas.height=800;//设置画布的高度
var cxt = canvas.getContext('2d');
createStar(cxt,4,100,300,400,400,10);
function createStar(context,n,r,R,x,y,lwid) {
/*
content 画图对象
n 星型顶点数
r 内圆半径
R 外圆半径
x 星型中心点x坐标
y 星型中心店y坐标
lwid lineWidth
*/
cxt.save();
cxt.lineWidth=lwid;
cxt.beginPath();
cxt.translate(x,y);
for(var i=0;iMath .cos(((1/4 + i)*2*Math.PI/n))*R,-Math.sin(((1/4 + i)*2*Math.PI/n))*R);
cxt.lineTo(Math.cos(((3/4 + i)*2*Math.PI/n))*r,-Math.sin(((3/4 + i)*2*Math.PI/n))*r);
}
cxt.closePath();
cxt.stroke();
cxt.restore();
}
script>
body>
html>