4_DeepLearnwP_IMDB_newswires_housePrices_Self-supervised_HoldOut_K-fold_L2_dropout_overfit_TP_metric

Classifying movie reviews: a binary classification example:

https://blog.csdn.net/Linli522362242/article/details/106433059

Classifying newswires: a multiclass classification example

https://blog.csdn.net/Linli522362242/article/details/106433059

Predicting house prices: a regression example(scalar regression and Cross_Validation)

https://blog.csdn.net/Linli522362242/article/details/106433059

02_End-to-End Machine Learning Project_StratifiedShuffleSplit_RMSE_MAE_Geographical Data_CaliforniaHouse

https://blog.csdn.net/Linli522362242/article/details/103387527

02_End-to-End Machine Learning Project_02_stats.sem_Cross_Validation_Grid_Randomized_Ensemble_ Pipeline

https://blog.csdn.net/Linli522362242/article/details/103587172

02_End-to-End Machine Learning Project_03_stats.sem_ppf_CategoricalEncoder_RandomizedSearchCV_joblib

https://blog.csdn.net/Linli522362242/article/details/103646927

03_Classification_02_confusion matrix _interpolation.shift正则表达_Multioutput Classification_Multilabel Classification_Build a spam classifier

https://blog.csdn.net/Linli522362242/article/details/103866244

06_Decision Trees_01_graphviz_Gini_Entropy_Decision Tree_CART_prune_Regression_Classification_Tree

https://blog.csdn.net/Linli522362242/article/details/104542381

##############################################################################################################

     After the three practical examples, you should be starting to feel familiar with how to approach classification and regression problems using neural networks, and you’ve witnessed the central problem of machine learning: overfitting. This chapter will formalize some of your new intuition into a solid conceptual framework for attacking and solving deep-learning problems. We’ll consolidate all of these concepts—model evaluation, data preprocessing and feature engineering, and tackling overfitting—into a detailed seven-step workflow for tackling any machine-learning task.

Four branches of machine learning

     In our previous examples, you’ve become familiar with three specific types of machine-learning problems: binary classification, multiclass classification, and scalar regression. All three are instances of supervised learning, where the goal is to learn the relationship between training inputs and training targets.

     Supervised learning is just the tip of the iceberg—machine learning is a vast field with a complex subfield taxonomy[tækˈsɑːnəmi]分类. Machine-learning algorithms generally fall into four broad categories, described in the following sections.

Supervised learning

     This is by far the most common case. It consists of learning to map input data to known targets (also called annotations标注), given a set of examples (often annotated by humans). All four examples you’ve encountered in this book so far were canonical examples of supervised learning. Generally, almost all applications of deep learning that are in the spotlight these days belong in this category, such as optical character recognition, speech recognition, image classification, and language translation.

     Although supervised learning mostly consists of classification and regression, there are more exotic[ɪɡˈzɑːtɪk]奇异的 variants变型 as well, including the following (with examples):

• Sequence generation—Given a picture, predict a caption describing it. Sequence generation can sometimes be reformulated as a series of classification problems (such as repeatedly predicting a word or token in a sequence).
   
• Syntax tree prediction—Given a sentence, predict its decomposition into a syntax tree.
   
• Object detection—Given a picture, draw a bounding box around certain objects inside the picture. This can also be expressed as a classification problem (given many candidate bounding boxes, classify the contents of each one) or as a joint classification and regression problem, where the bounding-box coordinates are predicted via vector regression.
   
• Image segmentation—Given a picture, draw a pixel-level mask掩模 on a specific object. (08_Dimensionality Reduction_02_Gaussian mixture_kmeans++_extent_tick_params_silhouette_image segmenthttps://blog.csdn.net/Linli522362242/article/details/105722461)

Unsupervised learning

     This branch of machine learning consists of finding interesting transformations of the input data without the help of any targets, for the purposes of data visualization, data compression, or data denoising, or to better understand the correlations present in the data at hand. Unsupervised learning is the bread and butter of data analytics, and it’s often a necessary step in better understanding a dataset before attempting to solve a supervised-learning problem. Dimensionality reduction(https://blog.csdn.net/Linli522362242/article/details/105722461) and clustering(https://blog.csdn.net/Linli522362242/article/details/105813977) are well-known categories of unsupervised learning.

Self-supervised learning

     This is a specific instance of supervised learning, but it’s different enough that it deserves its own category. Self-supervised learning is supervised learning without human-annotated labels—you can think of it as supervised learning without any humans in the loop. There are still labels involved (because the learning has to be supervised by something), but they’re generated from the input data, typically using a
heuristic[hjʊˈrɪstɪk]启发式的 algorithm.

     For instance, autoencoders自编码器 are a well-known instance of self-supervised learning, where the generated targets are the input, unmodified. In the same way, trying to predict the next frame in a video, given past frames, or the next word in a text, given previous
words, are instances of self-supervised learning (temporally supervised learning, in this case: supervision comes from future input data). Note that the distinction between supervised, self-supervised, and unsupervised learning can be blurry[ˈblɜːri]模糊的 sometimes—these categories are more of a continuum[数]连续统一 without solid borders. Self-supervised learning can be reinterpreted as either supervised or unsupervised learning, depending on whether you pay attention to the learning mechanism or to the context of its application.

#############################################################

NOTE

     In this book, we’ll focus specifically on supervised learning, because it’s by far the dominant form of deep learning today, with a wide range of
industry applications. We’ll also take a briefer look at self-supervised learning in later chapters.
#############################################################

Reinforcement learning

     Long overlooked, this branch of machine learning recently started to get a lot of attention after Google DeepMind successfully applied it to learning to play Atari games (and, later, learning to play Go围棋 at the highest level). In reinforcement learning, an agent receives information about its environment and learns to choose actions that will maximize some reward. For instance, a neural network that “looks”观察 at a videogame screen and outputs game actions in order to maximize its score can be trained via reinforcement learning.

     Currently, reinforcement learning is mostly a research area and hasn’t yet had significant practical successes beyond games. In time, however, we expect to see reinforcement learning take over an increasingly large range of real-world applications: self-driving cars, robotics, resource management, education, and so on. It’s an idea whose time has come, or will come soon.

Classification and regression glossary

     Classification and regression involve many specialized terms. You’ve come across some of them in earlier examples, and you’ll see more of them in future chapters. They have precise, machine-learning-specific definitions, and you should be familiar with them:

• Sample or input—One data point that goes into your model.
   
• Prediction or output—What comes out of your model.
   
• Target—The truth. What your model should ideally have predicted, according to an external source of data.
   
• Prediction error or loss value—A measure of the distance between your model’s prediction and the target.
   
• Classes—A set of possible labels to choose from in a classification problem. For example, when classifying cat and dog pictures, “dog” and “cat” are the two classes.
   
• Label—A specific instance of a class annotation in a classification problem. For instance, if picture #1234 is annotated as containing the class “dog,” then “dog” is a label of picture #1234.
   
• Ground-truth真值 or annotations—All targets for a dataset, typically collected by humans.
   
• Binary classification—A classification task where each input sample should be categorized into two exclusive categories.
   
• Multiclass classification—A classification task where each input sample should be categorized into more than two categories: for instance, classifying handwritten digits.
   
• Multilabel classification—A classification task where each input sample can be assigned multiple labels. For instance, a given image may contain both a cat and a dog and should be annotated both with the “cat” label and the “dog” label. The number of labels per image is usually variable.
   
• Scalar regression—A task where the target is a continuous scalar value. Predicting house prices is a good example: the different target prices form a continuous space.
   
• Vector regression—A task where the target is a set of continuous values: for example, a continuous vector. If you’re doing regression against multiple values (such as the coordinates of a bounding box in an image), then you’re doing vector regression.
   
• Mini-batch or batch—A small set of samples (typically between 8 and 128) that are processed simultaneously by the model. The number of samples is often a power of 2, to facilitate memory allocation on GPU. When training, a mini-batch is used to compute a single gradient-descent update applied to the weights of the model.

Evaluating machine-learning models

     In the three examples presented in chapter 3, we split the data into a training set, a validation set, and a test set. The reason not to evaluate the models on the same data they were trained on quickly became evident: after just a few epochs, all three models began to overfit. That is, their performance on never-before-seen data started stalling (or worsening) compared to their performance on the training data—which always
improves as training progresses.

     In machine learning, the goal is to achieve models that generalize—that perform well on never-before-seen data—and overfitting is the central obstacle障碍. You can only control that which you can observe, so it’s crucial to be able to reliably measure the generalization power of your model. The following sections look at strategies for mitigating减轻 overfitting and maximizing generalization. In this section, we’ll focus on how
to measure generalization: how to evaluate machine-learning models.

Training, validation, and test sets

     Evaluating a model always boils down to splitting the available data into three sets: training, validation, and test. You train on the training data and evaluate your model on the validation data. Once your model is ready for prime time, you test it one final time on the test data.

     You may ask, why not have two sets: a training set and a test set? You’d train on the training data and evaluate on the test data. Much simpler!

     The reason is that developing a model always involves tuning its configuration: for example, choosing the number of layers or the size of the layers (called the hyperparameters of the model, to distinguish them from the parameters, which are the network’s weights). You do this tuning by using as a feedback signal the performance of the model on the validation data. In essence, this tuning is a form of learning: a search for a good configuration in some parameter space. As a result, tuning the configuration of the model based on its performance on the validation set can quickly result in overfitting to the validation set, even though your model is never directly trained on it.

     Central to this phenomenon is the notion of information leaks. Every time you tune a hyperparameter of your model based on the model’s performance on the validation set, some information about the validation data leaks into the model. If you do this only once, for one parameter, then very few bits of information will leak, and your validation set will remain reliable to evaluate the model. But if you repeat this many times—running one experiment, evaluating on the validation set, and modifying your model as a result—then you’ll leak an increasingly significant amount of information about the validation set into the model.

     At the end of the day, you’ll end up with a model that performs artificially well on the validation data, because that’s what you optimized it for. You care about performance on completely new data, not the validation data, so you need to use a completely different, never-before-seen dataset to evaluate the model: the test dataset. Your model shouldn’t have had access to any information about the test set, even indirectly. If anything about the model has been tuned based on test set performance, then your measure of generalization will be flawed.

     Splitting your data into training, validation, and test sets may seem straightforward, but there are a few advanced ways to do it that can come in handy when little data is available. Let’s review three classic evaluation recipes: simple hold-out validation, Kfold validation, and iterated K-fold validation with shuffling.

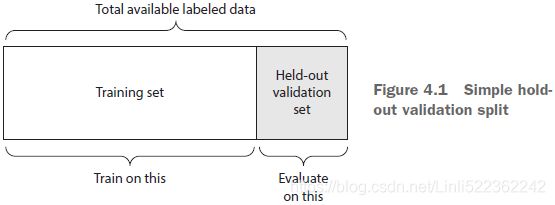
Simple Hold-out Validation

     Set apart some fraction of your data as your test set. Train on the remaining data, and evaluate on the test set. As you saw in the previous sections, in order to prevent information leaks, you shouldn’t tune your model based on the test set, and therefore you should also reserve a validation set.

     Schematically, hold-out validation looks like figure 4.1. The following listing shows a simple implementation.

Hold-out Validation

https://blog.csdn.net/Linli522362242/article/details/103387527 # Shuffle

https://blog.csdn.net/Linli522362242/article/details/105046444 # hold-out

num_validation_samples = 10000

import numpy as np

np.random.shuffle(data)                         #Shuffling the data is usually appropriate
validation_data = data[:num_validation_samples] #Defines the validation set
data = data[num_validation_samples:]

training_data = data[:] #Defines the training set

model = get_model() #Trains a model on the training data, and evaluates it on the validation data
model.train(training_data)
validation_score = model.evalute( validation_data )

# At this point you can tune your model,
# retrain it, evaluate it, tune it again...

# Once you've tuned your hyperparameters, it's common to train your final model from scratch
# on all non-test data available
model = get_model()
model.train( np.concatenatete([training_data, validation_data])
           )

test_score = model.evaluate( test_data ) 

     This is the simplest evaluation protocol, and it suffers from one flaw[flɔː]瑕疵 if little data is available, then your validation and test sets may contain too few samples to be statistically representative of the data at hand. This is easy to recognize: if different random shuffling rounds of the data before splitting end up yielding very different measures of model performance, then you’re having this issue. K-fold validation and iterated K-fold validation are two ways to address this, as discussed next.

K-fold Validation

     With this approach, you split your data into K partitions of equal size. For each partition i, train a model on the remaining K – 1 partitions, and evaluate it on partition i. Your final score is then the averages of the K scores obtained. This method is helpful when the performance of your model shows significant variance变化很大 based on your train-test split. Like hold-out validation, this method doesn’t exempt [ɪɡˈzempt]使豁免 you from using a distinct validation set for model calibration校准.

     Schematically, K-fold cross-validation looks like figure 4.2. Listing 4.2 shows a simple implementation.

Figure 4.2 Three-fold validation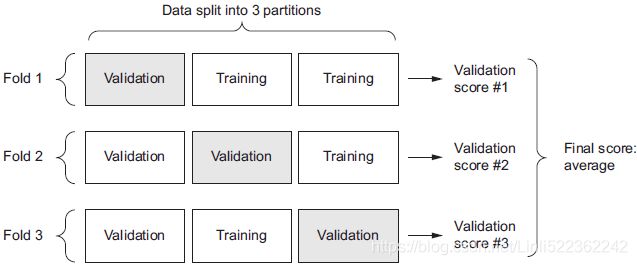

k = 4
num_validation_samples = len(data)//k

np.random.shuffle(data)

validation_scores = []
for fold in range(k):
    # Selects the validation data partition
    validation_data = data[ num_validation_samples*fold : num_validation_samples*(fold+1)]
    # Uses the remainder of the data as training data. Note that the + operator is 
    # list concatenation, not summation.
    training_data = data[:num_validation_samples * fold] + 
                    data[num_validation_samples*(fold+1):]
    
    # Creates a brand-new instance of the model (untrained)
    model = get_model()
    model.train( training_data )
    
    validation_score = model.evaluate(validation_data)
    validation_scores.append( validation_score )

# Validation score: average of the validation scores of the k folds
validation_score = np.average( validation_scores )

# Trains the final model on all non-test data available
model = get_model()
model.train( data )

test_score = model.evaluate(test_data)

Iterated K-fold Validation with Shuffling

     This one is for situations in which you have relatively little data available and you need to evaluate your model as precisely as possible. I’ve found it to be extremely helpful in Kaggle competitions. It consists of applying K-fold validation multiple times(P), shuffling the data every time before splitting it K ways. The final score is the average of the scores obtained at each run of K-fold validation. Note that you end up training and evaluating P × K models (where P is the number of iterations you use), which can very expensive.

Things to keep in mind

Keep an eye out for the following when you’re choosing an evaluation protocol:

• Data representativeness—You want both your training set and test set to be representative of the data at hand. For instance, if you’re trying to classify images of digits, and you’re starting from an array of samples where the samples are ordered by their class, taking the first 80% of the array as your training set and the remaining 20% as your test set will result in your training set containing only classes 0–7, whereas your test set contains only classes 8–9. This seems like a ridiculous mistake, but it’s surprisingly common. For this reason, you usually should randomly shuffle your data before splitting it into training and test sets.
   
• The arrow of time—If you’re trying to predict the future given the past (for example, tomorrow’s weather, stock movements, and so on), you should not randomly shuffle your data before splitting it, because doing so will create a temporal leak时间泄露: your model will effectively be trained on data from the future. In such situations, you should always make sure all data in your test set is posterior to the data in the training set.
   
• Redundancy in your data—If some data points in your data appear twice (fairly common with real-world data), then shuffling the data and splitting it into a training set and a validation set will result in redundancy between the training and validation sets. In effect, you’ll be testing on part of your training data, which is the worst thing you can do! Make sure your training set and validation set are disjoint.

Data preprocessing, feature engineering, and feature learning

     In addition to model evaluation, an important question we must tackle before we dive deeper into model development is the following: how do you prepare the input data and targets before feeding them into a neural network? Many data-preprocessing and feature-engineering techniques are domain specific (for example, specific to text data or image data); we’ll cover those in the following chapters as we encounter them in
practical examples. For now, we’ll review the basics that are common to all data domains.

Data preprocessing for neural networks

     Data preprocessing aims at making the raw data at hand more amenable[əˈminəbəl, əˈmɛnə-]可用某种方式处理的 to neural networks. This includes vectorization, normalization, handling missing values, and feature extraction.

Vectorization

     All inputs and targets in a neural network must be tensors of floating-point data (or, in specific cases, tensors of integers). Whatever data you need to process—sound, images, text—you must first turn into tensors, a step called data vectorization. For instance, in the two previous text-classification examples, we started from text represented as lists of integers (standing for sequences of words), and we used one-hot encoding to turn them into a tensor of float32 data. In the examples of classifying digits and predicting house prices, the data already came in vectorized form, so you were able to skip this step.

Value Normalization

     In the digit-classification example, you started from image data encoded as integers in the 0–255 range, encoding grayscale values. Before you fed this data into your network, you had to cast it to float32 and divide by 255 so you’d end up with floatingpoint values in the 0–1 range. Similarly, when predicting house prices, you started from features that took a variety of ranges—some features had small floating-point values,
others had fairly large integer values. Before you fed this data into your network, you had to normalize each feature independently so that it had a standard deviation of 1 and a mean of 0.

     In general, it isn’t safe to feed into a neural network data that takes relatively large values (for example, multidigit integers, which are much larger than the initial values taken by the weights of a network) or data that is heterogeneous[ˌhetərəˈdʒi:niəs]成分混杂的 (for example, data where one feature is in the range 0–1 and another is in the range 100–200). Doing so can trigger large gradient updates that will prevent the network from converging. To make learning easier for your network, your data should have the following characteristics:

• Take small values—Typically most values should be in the 0–1 range.
• Be homogenous—That is, all features should take values in roughly the same range.

     Additionally, the following stricter normalization practice is common and can help, although it isn’t always necessary (for example, you didn’t do this in the digit-classification example):

• Normalize each feature independently to have a mean of 0.
• Normalize each feature independently to have a standard deviation of 1.

This is easy to do with Numpy arrays:

x -= x.mean(axis=0) # Assuming x is a 2D data matrix of shape (samples, features)
x /= x.std(axis=0)

Handling Missing Value

     You may sometimes have missing values in your data. For instance, in the house-price example, the first feature (the column of index 0 in the data) was the per capita人均 crime rate. What if this feature wasn’t available for all samples? You’d then have missing values in the training or test data.

     In general, with neural networks, it’s safe to input missing values as 0, with the condition that 0 isn’t already a meaningful value. The network will learn from exposure to the data that the value 0 means missing data and will start ignoring the value.

     Note that if you’re expecting missing values in the test data, but the network was trained on data without any missing values, the network won’t have learned to ignore missing values! In this situation, you should artificially generate training samples with missing entries: copy some training samples several times, and drop some of the features that you expect are likely to be missing in the test data.

Feature engineering

    Feature engineering is the process of using your own knowledge about the data and about the machine-learning algorithm at hand (in this case, a neural network) to make the algorithm work better by applying hardcoded (nonlearned) transformations to the data before it goes into the model. In many cases, it isn’t reasonable to expect a machinelearning model to be able to learn from completely arbitrary data. The data needs to be presented to the model in a way that will make the model’s job easier.

     Let’s look at an intuitive example. Suppose you’re trying to develop a model that can take as input an image of a clock and can output the time of day (see figure 4.3).

Figure 4.3 Feature engineering for reading the time on a clock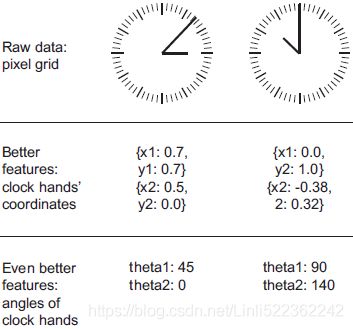

     If you choose to use the raw pixels of the image as input data, then you have a difficult machine-learning problem on your hands. You’ll need a convolutional neural network to solve it, and you’ll have to expend quite a bit of computational resources to train the network.

     But if you already understand the problem at a high level (you understand how humans read time on a clock face), then you can come up with much better input features for a machine-learning algorithm: for instance, it’s easy to write a five-line Python script to follow the black pixels of the clock hands and output the (x, y) coordinates of the tip of each hand. Then a simple machine-learning algorithm can learn to associate these coordinates with the appropriate time of day.

     You can go even further: do a coordinate change, and express the (x, y) coordinates as polar coordinates with regard to the center of the image. Your input will become the angle theta of each clock hand. At this point, your features are making the problem so easy that no machine learning is required; a simple rounding operation and dictionary lookup are enough to recover the approximate time of day.

     That’s the essence of feature engineering: making a problem easier by expressing it in a simpler way. It usually requires understanding the problem in depth.

     Before deep learning, feature engineering used to be critical, because classical shallow浅的 algorithms didn’t have hypothesis spaces rich enough to learn useful features by themselves. The way you presented the data to the algorithm was essential to its success. For instance, before convolutional[kɒnvə'luʃənəl]卷积 neural networks became successful on the MNIST digit-classification problem, solutions were typically based on hardcoded features such as the number of loops in a digit image, the height of each digit in an image, a histogram of pixel values, and so on.

      Fortunately, modern deep learning removes the need for most feature engineering, because neural networks are capable of automatically extracting useful features from raw data. Does this mean you don’t have to worry about feature engineering as long as you’re using deep neural networks? No, for two reasons:

• Good features still allow you to solve problems more elegantly[ˈɛləɡəntlɪ]高雅地 while using fewer resources. For instance, it would be ridiculous可笑的 to solve the problem of reading a clock face using a convolutional neural network.
   
• Good features let you solve a problem with far less data. The ability of deep learning models to learn features on their own relies on having lots of training data available; if you have only a few samples, then the information value in their features becomes critical.

Overfitting and underfitting

     In all three examples in the previous chapter—predicting movie reviews, topic classification, and house-price regression—the performance of the model on the held-out validation data always peaked after a few epochs and then began to degrade: the model quickly started to overfit to the training data. Overfitting happens in every machine-learning problem. Learning how to deal with overfitting is essential to mastering machine learning.

     The fundamental issue in machine learning is the tension矛盾 between optimization and generalization. Optimization refers to the process of adjusting a model to get the best performance possible on the training data (the learning in machine learning), whereas generalization refers to how well the trained model performs on data it has never seen before. The goal of the game is to get good generalization, of course, but you don’t control generalization; you can only adjust the model based on its training data.

     At the beginning of training, optimization and generalization are correlated: the lower the loss on training data, the lower the loss on test data. While this is happening, your model is said to be underfit: there is still progress to be made; the network hasn’t yet modeled all relevant patterns in the training data. But after a certain number of iterations on the training data, generalization stops improving, and validation metrics stall停顿 and then begin to degrade: the model is starting to overfit. That is, it’s beginning to learn patterns that are specific to the training data but that are misleading or irrelevant when it comes to new data.

     To prevent a model from learning misleading or irrelevant patterns found in the training data, the best solution is to get more training data. A model trained on more data will naturally generalize better. When that isn’t possible, the next-best solution is to modulate the quantity of information that your model is allowed to store or to add constraints on what information it’s allowed to store. If a network can only afford to memorize a small number of patterns, the optimization process will force it to focus on the most prominent patterns, which have a better chance of generalizing well.

     The processing of fighting overfitting this way is called regularization. Let’s review some of the most common regularization techniques and apply them in practice to improve the movie-classification model from 3.4 https://blog.csdn.net/Linli522362242/article/details/106433059

 Reducing the network's size

Reducing the network’s size-->the number of learnable parameters in the model -->the number of layers and the number of units per layer

     The simplest way to prevent overfitting is to reduce the size of the model: the number of learnable parameters in the model (which is determined by the number of layers and the number of units per layer). In deep learning, the number of learnable parameters in a model is often referred to as the model’s capacity[kəˈpæsəti]容量. Intuitively, a model with more parameters has more memorization capacity and therefore can easily learn a perfect dictionary-like mapping between training samples and their targets—a mapping without any generalization power. For instance, a model with 500,000 binary parameters could easily be made to learn the class of every digit in the MNIST training set: we’d need only 10 binary parameters for each of the 50,000 digits. But such a model would be useless for classifying new digit samples. Always keep this in mind: deeplearning models tend to be good at fitting to the training data, but the real challenge is generalization, not fitting.

     On the other hand, if the network has limited memorization resources, it won’t be able to learn this mapping as easily; thus, in order to minimize its loss, it will have to resort凭借 to learning compressed representations that have predictive power regarding关于 the targets—precisely the type of representations we’re interested in. At the same time, keep in mind that you should use models that have enough parameters that they don’t underfit: your model shouldn’t be starved for memorization resources. There is a compromise折中 to be found between too much capacity and not enough capacity.

     Unfortunately, there is no magical formula to determine the right number of layers or the right size for each layer. You must evaluate an array of different architectures (on your validation set, not on your test set, of course) in order to find the correct model size for your data. The general workflow to find an appropriate model size is to start with relatively few layers and parameters, and increase the size of the layers or add new layers until you see diminishing returns收益递减 with regard to validation loss直到这种增加对验证损失的影响变得很小.

Let’s try this on the movie-review classification network. The original network is shown next.

https://blog.csdn.net/Linli522362242/article/details/106433059

from tensorflow.keras.datasets import imdb
                                        # select top 10,000 most frequently occurring words
( train_data, train_labels), (test_data, test_labels) = imdb.load_data( num_words=10000 ) 

# You can’t feed lists of integers into a neural network. You have to turn your lists
# (train_data and test_data) into tensors.

# Encoding the integer sequences into a binary matrix
import numpy as np
# sequences.shape==(samples, indices of words)
def vectorize_sequences( sequences, dimension = 10000 ):
    results = np.zeros( (len(sequences), dimension) )
    for i, sequence in enumerate(sequences):
        #Set the position corresponding to the index of word in each sample to 1.0
        results[i, sequence] = 1.
    return results

x_train = vectorize_sequences( train_data )
x_test = vectorize_sequences( test_data )

# convert the dataset to array then
# give the dense layer the ability to handle floating-point vector data
y_train = np.asarray( train_labels).astype('float32')
y_test = np.asarray( test_labels).astype('float32')


import tensorflow as tf
tf.random.set_seed(42)
np.random.seed(42)

####################################
model_ori = keras.models.Sequential()
model_ori.add( keras.layers.Dense(16, activation = 'relu', input_shape=(10000,)
                       )
         )
model_ori.add( keras.layers.Dense(16, activation = 'relu') )
model_ori.add( keras.layers.Dense(1, activation = 'sigmoid') )
####################################

from tensorflow.keras import optimizers


model_ori.compile( optimizer=optimizers.RMSprop(lr=0.001), loss='binary_crossentropy', 
                  metrics=['accuracy'] )
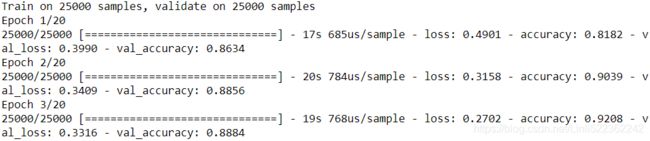
history_ori = model_ori.fit( x_train_partial, y_train_partial, epochs=20, batch_size=512,
                     validation_data=(x_val, y_val)
                   )

 
... ...

Now let’s try to replace it with this smaller network.

     Version of the model with lower capacity(-->the number of learnable parameters in the model -->the number of layers and the number of units per layer)

# facing a binary classification problem and the output of your network is a probability 
# (you end your network with a single-unit layer with a sigmoid activation)

model_small = keras.models.Sequential()
model_small.add( keras.layers.Dense(4, activation='relu', input_shape=(10000,)
                             ) # relu: (0, max(z))=(0, dot(W, input) + b) )
         )
model_small.add( keras.layers.Dense(4, activation='relu') )
#sigmoid: outputting something that can be interpreted as a probability. #between 0 and 1
model_small.add( keras.layers.Dense(1, activation='sigmoid') ) # σ(z) = 1 / (1 + exp(–z))

model_small.compile( optimizer=optimizers.RMSprop(lr=0.001), loss='binary_crossentropy',
                     metrics=['accuracy']
                   )
history_small = model_small.fit( x_train, y_train, epochs=20, batch_size=512, 
                           validation_data = (x_test, y_test)
                         )

... ...

import matplotlib.pyplot as plt

history_dict_ori=history_ori.history
val_loss_ori = history_dict_ori['val_loss']

history_dict_small=history_small.history
val_loss_small = history_dict_small['val_loss']

epochs = range(1, len(val_loss_ori) +1)

plt.plot(epochs, val_loss_ori, 'b+', label='Original model')
plt.plot(epochs, val_loss_small, 'bo', label='Smaller model')
plt.title('Figure 4.4 Effect of model capacity on validation loss: trying a smaller model')
plt.xlabel('Epochs')
plt.ylabel('Validation_loss')
plt.legend()
plt.show()

     Figure 4.4 shows a comparison of the validation losses of the original network and the smaller network. The dots are the validation loss values of the smaller network, and the crosses are the initial network (remember, a lower validation loss signals a better model). 

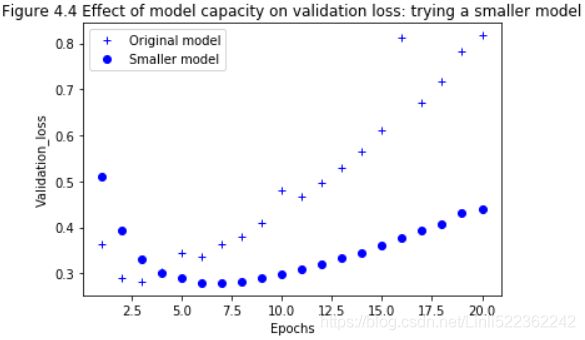# more time to best fit and 

     As you can see, the smaller network starts overfitting later than the reference network (after six epochs rather than four), and its performance degrades more slowly(the loss increases more slowly) once it starts overfitting.

plt.clf() # clears the figure

val_acc_ori = history_dict_ori['val_accuracy']

val_acc_small = history_dict_small['val_accuracy']

epochs = range(1, len(val_acc_ori) +1)

plt.plot(epochs, val_acc_ori, 'b+', label='Original model')
plt.plot(epochs, val_acc_small, 'bo', label='Smaller model')
plt.title('Figure 4.4 Effect of model capacity on validation accuracy: trying a smaller model')
plt.xlabel('Epochs')
plt.ylabel('Validation_accuracy')
plt.legend()
plt.show()

Proved: a lower validation loss(higher accuracy) signals a better model

Now, for kicks, let’s add to this benchmark a network that has much more capacity—far more than the problem warrants.

     Version of the model with higher capacity(-->the number of learnable parameters in the model -->the number of layers and the number of units per layer)

# facing a binary classification problem and the output of your network is a probability 
# (you end your network with a single-unit layer with a sigmoid activation)

model_big = keras.models.Sequential()
model_big.add( keras.layers.Dense(512, activation='relu', input_shape=(10000,)
                             ) # relu: (0, max(z))=(0, dot(W, input) + b) )
         )
model_big.add( keras.layers.Dense(512, activation='relu') )
#sigmoid: outputting something that can be interpreted as a probability. #between 0 and 1
model_big.add( keras.layers.Dense(1, activation='sigmoid') ) # σ(z) = 1 / (1 + exp(–z))

model_big.compile( optimizer=optimizers.RMSprop(lr=0.001), loss='binary_crossentropy',
                     metrics=['accuracy']
                   )
history_big = model_big.fit( x_train_partial, y_train_partial, epochs=20, batch_size=512, 
                           validation_data = (x_test, y_test)
                         )

 
... ...

import matplotlib.pyplot as plt

history_dict_ori=history_ori.history
val_loss_ori = history_dict_ori['val_loss']

history_dict_big=history_big.history
val_loss_big = history_dict_big['val_loss']

epochs = range(1, len(val_loss_ori) +1)

plt.plot(epochs, val_loss_ori, 'b+', label='Original model')
plt.plot(epochs, val_loss_big, 'bo', label='Bigger model')
plt.title('Figure 4.5 Effect of model capacity on validation loss: trying a bigger model')
plt.xlabel('Epochs')
plt.ylabel('Validation_loss')
plt.ylim(0,1.6)
plt.legend(loc='upper left')
plt.show()

     Figure 4.5 shows how the bigger network fares compared to the reference network. The dots are the validation loss values of the bigger network, and the crosses are the initial network. Its validation loss is also noisier.

     The bigger network starts overfitting almost immediately, and it overfits much more severely.

import matplotlib.pyplot as plt

history_dict_ori=history_ori.history
train_loss_ori = history_dict_ori['loss']

history_dict_big=history_big.history
train_loss_big = history_dict_big['loss']

epochs = range(1, len(val_loss_ori) +1)

plt.plot(epochs, train_loss_ori, 'b+', label='Original model')
plt.plot(epochs, train_loss_big, 'bo', label='Bigger model')
plt.title('Figure 4.6 Effect of model capacity on training loss: trying a bigger model')
plt.xlabel('Epochs')
plt.ylabel('Training_loss')
plt.ylim(-0.2,0.6)
plt.legend(loc='upper right')
plt.show()

     Meanwhile, figure 4.6 shows the training losses for the two networks. As you can see, the bigger network gets its training loss near zero very quickly. The more capacity the network has, the more quickly it can model the training data (resulting in a low training loss), but the more susceptible易受影响的 it is to overfitting (resulting in a large difference between the training and validation loss).
 # the bigger network gets its training loss near zero very quickly

Adding weight regularization

     You may be familiar with the principle of Occam’s razor: given two explanations for something, the explanation most likely to be correct is the simplest one—the one that makes fewer assumptions. This idea also applies to the models learned by neural networks: given some training data and a network architecture, multiple sets of weight values (multiple models) could explain the data. Simpler models are less likely to overfit
than complex ones.

    A simple model in this context is a model where the distribution of parameter values has less entropy (or a model with fewer parameters, as you saw in the previous section). Thus a common way to mitigate overfitting is to put constraints on the complexity of a network by forcing its weights to take only small values, which makes the distribution of weight values more regular. This is called weight regularization, and it’s
done by adding to the loss function of the network a cost associated with having large weights. This cost comes in two flavors:

• L1 regularization—The cost added is proportional to the absolute value of the weight coefficients (the L1 norm of the weights).
• L2 regularization—The cost added is proportional to the square of the value of the weight coefficients (the L2 norm of the weights). L2 regularization is also called weight decay衰减 in the context of neural networks. Don’t let the different name confuse you: weight decay is mathematically the same as L2 regularization. 

     In Keras, weight regularization is added by passing weight regularizer instances to layers as keyword arguments. Let’s add L2 weight regularization to the movie-review classification network.

from tensorflow.keras import regularizers

model_l2 = keras.models.Sequential()
model_l2.add( keras.layers.Dense(16, kernel_regularizer = regularizers.l2(0.001), #0.001*weight_coefficient_value
                              activation = 'relu', input_shape=(10000,)
                             )
            )
model_l2.add( keras.layers.Dense(16, kernel_regularizer = regularizers.l2(0.001),
                              activation = 'relu'
                             )
            )
model_l2.add( keras.layers.Dense(1, activation = 'sigmoid')
            )

import tensorflow as tf
tf.random.set_seed(42)
np.random.seed(42)

model_l2.compile( optimizer=optimizers.RMSprop(lr=0.001), loss='binary_crossentropy',
                     metrics=['accuracy']
                )
history_l2 = model_l2.fit( x_train, y_train, epochs=20, batch_size=512, 
                           validation_data = (x_test, y_test)
                         )

 
... ...

     l2(0.001) means every coefficient in the weight matrix of the layer will add 0.001* weight_coefficient_value to the total loss of the network. Note that because this penalty is only added at training time, the loss for this network will be much higher at training than at test time.

import matplotlib.pyplot as plt

history_dict_ori=history_ori.history
val_loss_ori = history_dict_ori['val_loss']

history_dict_l2=history_l2.history
val_loss_l2 = history_dict_l2['val_loss']

epochs = range(1, len(val_loss_l2) +1)

plt.plot(epochs, val_loss_ori, 'b+', label='Original model')
plt.plot(epochs, val_loss_l2, 'bo', label='Model with L2')
plt.title('Figure 4.7 Effect of L2 weight regularization on validation loss')
plt.xlabel('Epochs')
plt.ylabel('Validation Loss')
plt.legend()
plt.show()

    Figure 4.7 shows the impact of the L2 regularization penalty. As you can see, the model with L2 regularization (dots) has become much more resistant有抵抗力的 to overfitting than the reference model (crosses), even though both models have the same number of parameters. 
 # the loss on mode with L2 norm << the loss on original model

As an alternative to L2 regularization, you can use one of the following Keras weight regularizers.

Different weight regularizers available in Keras

from tensorflow.keras import regularizers

regularizers.l1(0.001) #L1 regularization
regularizers.l1_l2(l1=0.001, l2=0.001)

Adding dropout掉队

     Dropout is one of the most effective and most commonly used regularization techniques for neural networks, developed by Geoff Hinton and his students at the University of Toronto. Dropout, applied to a layer, consists of randomly dropping out (setting to zero) a number of output features of the layer during training. Let’s say a given layer would normally return a vector [0.2, 0.5, 1.3, 0.8, 1.1] for a given input sample during training. After applying dropout, this vector will have a few zero entries distributed at random: for example, [0, 0.5, 1.3, 0, 1.1]. The dropout rate is the fraction of the features that are zeroed out是被设为0 的特征所占的比例; it’s usually set between 0.2 and 0.5. At test time, no units are dropped out; instead, the layer’s output values are scaled down by a factor equal to the dropout rate, to balance for the fact that more units are active than at training time.

     Consider a Numpy matrix containing the output of a layer, layer_output, of shape (batch_size, features). At training time, we zero out设为0 at random a fraction of the values in the matrix:

At training time, drops out 50% of the units in the output

layer_output *= np.random.randint(0, high=2, size=layer_output.shape) #[low=0, high) ==> 0 or 1  
# At training time, drops out 50% of the units in the output

At test time, we scale down the output by the dropout rate. Here, we scale by 0.5 (because we previously dropped half the units):

layer_output *= 0.5  # At test time

     Note that this process can be implemented by doing both operations at training time and leaving the output unchanged at test time, which is often the way it’s implemented in practice (see figure 4.8):

layer_output *= np.random.randint( 0,high=2, size=layer_output.shape ) # At training time
layer_output /=0.5 # Note that we’re scaling up rather scaling down in this case.

     Figure 4.8 Dropout applied to an activation matrix at training time, with rescaling happening during training. At test time, the activation matrix is unchanged.

     This technique may seem strange and arbitrary. Why would this help reduce overfitting? Hinton says he was inspired by, among other things, a fraud-prevention mechanism used by banks. In his own words, “I went to my bank. The tellers kept changing and I asked one of them why. He said he didn’t know but they got moved around a lot. I figured it must be because it would require cooperation between employees to successfully
defraud the bank. This made me realize that randomly removing a different subset of neurons on each example would prevent
conspiracies [kənˈspirəsiz]密谋 and thus reduce overfitting.” The core idea is that introducing noise in the output values of a layer can
break up happenstance偶然 patterns that aren’t significant (what Hinton refers to as conspiracies), which the network will start memorizing if no noise is present.

In Keras, you can introduce dropout in a network via the Dropout layer, which is applied to the output of the layer right before it:

model.add(layers.Dropout(0.5))

Let’s add two Dropout layers in the IMDB network to see how well they do at reducing overfitting.

Adding dropout to the IMDB network

model_dropout = keras.models.Sequential()
model_dropout.add(keras.layers.Dense(16, activation='relu', input_shape=(10000,)))#10000 dimensions
model_dropout.add( keras.layers.Dropout(0.5) )
model_dropout.add( keras.layers.Dense(16, activation='relu') )
model_dropout.add( keras.layers.Dropout(0.5) )
model_dropout.add( keras.layers.Dense(1, activation='sigmoid') )

tf.random.set_seed(42)
np.random.seed(42)

model_dropout.compile( optimizer='RMSprop', loss='binary_crossentropy', metrics=['accuracy'] )
history_dropout = model_dropout.fit( x_train, y_train, epochs=20, batch_size=512,
                                     validation_data = (x_test, y_test)
                                   )

... ...

history_dict_ori = history_ori.history
val_loss_ori = history_dict_ori['val_loss']

history_dict_dropout = history_dropout.history
val_loss_dropout = history_dict_dropout['val_loss']

epochs = range(1, len(val_loss_ori) + 1)

plt.plot(epochs, val_loss_ori, 'b+', label='Original model')
plt.plot(epochs, val_loss_dropout, 'bo', label='Model with dropout')
plt.title('Figure 4.9 Figure 4.9 Effect of dropout on validation loss')
plt.xlabel("Epochs")
plt.ylabel('Validation Loss')
plt.legend()
plt.show()

 Figure 4.9 shows a plot of the results. Again, this is a clear improvement over the reference network.
 # the loss on mode with dropout layers < the loss on original model

To recap扼要重述, these are the most common ways to prevent overfitting in neural networks:

• Get more training data.
• Reduce the capacity of the network. (-->the number of learnable parameters in the model -->the number of layers and the number of units per layer)
• Add weight regularization.
• Add dropout.

The universal workflow of machine learning

     In this section, we’ll present a universal blueprint that you can use to attack and solve any machine-learning problem. The blueprint ties together the concepts you’ve learned about in this chapter: problem definition, evaluation, feature engineering, and fighting overfitting.

Defining the problem and assembling a dataset

First, you must define the problem at hand:

• What will your input data be? What are you trying to predict? You can only learn to predict something if you have available training data: for example, you can only learn to classify the sentiment情感 of movie reviews if you have both movie reviews and sentiment annotations available. As such, data availability is usually the limiting factor at this stage (unless you have the means财富/手段 to pay people to collect data for you).
   
• What type of problem are you facing? Is it binary classification? Multiclass classification? Scalar regression? Vector regression? Multiclass, multilabel classification? Something else, like clustering, generation, or reinforcement learning? Identifying the problem type will guide your choice of model architecture, loss function, and so on.

     You can’t move to the next stage until you know what your inputs and outputs are, and what data you’ll use. Be aware of the hypotheses you make at this stage:

• You hypothesize that your outputs can be predicted given your inputs.
   
• You hypothesize that your available data is sufficiently informative to learn the relationship between inputs and outputs.

     Until you have a working model, these are merely hypotheses, waiting to be validated or invalidated. Not all problems can be solved; just because you’ve assembled examples of inputs X and targets Y doesn’t mean X contains enough information to predict Y. For instance, if you’re trying to predict the movements of a stock on the stock market given its recent price history, you’re unlikely to succeed, because price history
doesn’t contain much predictive information.

     One class of unsolvable problems you should be aware of is nonstationary problems非平稳问题. Suppose you’re trying to build a recommendation engine for clothing, you’re training it on one month of data (August), and you want to start generating recommendations
in the winter. One big issue is that the kinds of clothes people buy change from season to season: clothes buying is a nonstationary phenomenon over the scale of a few months. What you’re trying to model changes over time. In this case, the right move is to constantly retrain your model on data from the recent past, or gather data at a timescale where the problem is stationary. For a cyclical problem like clothes buying, a few years’ worth of data will suffice[səˈfaɪs]使有能力 to capture seasonal variation—but remember to make the time of the year an input of your model!

     Keep in mind that machine learning can only be used to memorize patterns that are present in your training data. You can only recognize what you’ve seen before. Using machine learning trained on past data to predict the future is making the assumption that the future will behave like the past. That often isn’t the case.

Choosing a measure of success

     To control something, you need to be able to observe it. To achieve success, you must define what you mean by success—accuracy? Precision and recall? Customer-retention rate客户保留率? Your metric for success will guide the choice of a loss function: what your model will optimize. It should directly align with your higher-level goals, such as the success of your business.
##############################################
https://blog.csdn.net/Linli522362242/article/details/103786116
T: True prediction or classify correctly;     F: False prediction or classify incorrectly
P: instance is truely belong to target class based on the fact;     
N: instance is not belong to target class based on the fact
Accuracy = (TP+TN)/(TP+FP+FN+TN)
Precision = TP/(TP+FP) # True predicted/ (True predicted + False predicted)
Recall = TP/(TP+FN)  ==  

the ROC curve plots sensitivity (recall==TP/(TP+FN) ) versus 1 – specificity(TNR).==FPR
            #Xs, Ys 
plt.plot(fpr,  tpr, lw=2, label=label)

     One way to compare classifiers is to measure the area under the curve (AUC). A perfect classifier will have a ROC AUC equal to 1, whereas a purely random classifier will have a ROC AUC equal to 0.5. 
https://blog.csdn.net/Linli522362242/article/details/103786116
##############################################

metrics

• For balanced-classification problems, where every class is equally likely每个类别的可能性相同, accuracy and area under the receiver operating characteristic curve (ROC AUC) are common metrics.
   
• For class-imbalanced problems, you can use precision and recall.
   
• For ranking problems or multilabel classification, you can use mean average precision.

And it isn’t uncommon to have to define your own custom metric by which to measure success. To get a sense
of the diversity of machine-learning success metrics and how they relate to different problem domains, it’s helpful to browse the data science competitions on Kaggle (https://kaggle.com); they showcase a wide range of problems and evaluation metrics.

Deciding on an evaluation protocol

      Once you know what you’re aiming for, you must establish how you’ll measure your current progress. We’ve previously reviewed three common evaluation protocols:

• Maintaining a hold-out validation set—The way to go when you have plenty of data
   
• Doing K-fold cross-validation—The right choice when you have too few samples for hold-out validation to be reliable
   
• Doing iterated K-fold validation—For performing highly accurate model evaluation when little data is available

Just pick one of these. In most cases, the first will work well enough.

Preparing your data

     Once you know what you’re training on, what you’re optimizing for, and how to evaluate your approach, you’re almost ready to begin training models. But first, you should format your data in a way that can be fed into a machine-learning model—here, we’ll assume a deep neural network:

• As you saw previously, your data should be formatted as tensors.
   
• The values taken by these tensors should usually be scaled to small values: for example, in the [-1, 1] range or [0, 1] range.
   
• If different features take values in different ranges (heterogeneous data), then the data should be normalized.
   
• You may want to do some feature engineering, especially for small-data problems.

Once your tensors of input data and target data are ready, you can begin to train models.

Developing a model that does better than a baseline

     Your goal at this stage is to achieve statistical power统计功效 : that is, to develop a small model that is capable of beating a dumb baseline. In the MNIST digit-classification example, anything that achieves an accuracy greater than 0.1 can be said to have statistical power; in the IMDB example, it’s anything with an accuracy greater than 0.5.

     Note that it’s not always possible to achieve statistical power. If you can’t beat a random baseline after trying multiple reasonable architectures, it may be that the answer to the question you’re asking isn’t present in the input data. Remember that you make two hypotheses:

• You hypothesize that your outputs can be predicted given your inputs.
• You hypothesize that the available data is sufficiently informative to learn the relationship between inputs and outputs.

It may well be that these hypotheses are false, in which case you must go back to the drawing board.

Assuming that things go well, you need to make three key choices to build your first working model:

• Last-layer activation—This establishes useful constraints on the network’s output. For instance, the IMDB classification example used sigmoid in the last layer; the regression example didn’t use any last-layer activation; and so on.
   
• Loss function—This should match the type of problem you’re trying to solve. For instance, the IMDB example used binary_crossentropy, the regression example used mse, and so on.
   
• Optimization configuration—What optimizer will you use? What will its learning rate be? In most cases, it’s safe to go with rmsprop and its default learning rate.

     Regarding the choice of a loss function, note that it isn’t always possible to directly optimize for the metric that measures success on a problem. Sometimes there is no easy way to turn a metric into a loss function; loss functions, after all, need to be computable given only a mini-batch of data (ideally, a loss function should be computable for as little as a single data point) and must be differentiable (otherwise, you can’t use backpropagation反向传播https://blog.csdn.net/Linli522362242/article/details/106433059 to train your network). For instance, the widely used classification metric ROC AUC can’t be directly optimized. Hence, in classification tasks, it’s common to optimize for a proxy metric of ROC AUC, such as crossentropy. In general, you can hope that the lower the crossentropy gets, the higher the ROC AUC will be.

Table 4.1 can help you choose a last-layer activation and a loss function for a few common problem types.

Table 4.1 Choosing the right last-layer activation and loss function for your model

Scaling up: developing a model that overfits

     Once you’ve obtained a model that has statistical power统计功效, the question becomes, is your model sufficiently powerful? Does it have enough layers and parameters to properly model the problem at hand? For instance, a network with a single hidden layer with two units would have statistical power on MNIST but wouldn’t be sufficient to solve the problem well. Remember that the universal tension矛盾 in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it.

To figure out how big a model you’ll need, you must develop a model that overfits.
This is fairly easy:
1 Add layers.
2 Make the layers bigger.
3 Train for more epochs.

     Always monitor the training loss and validation loss, as well as the training and validation values for any metrics you care about. When you see that the model’s performance on the validation data begins to degrade, you’ve achieved overfitting.

     The next stage is to start regularizing and tuning the model, to get as close as possible to the ideal model that neither underfits nor overfits.

Regularizing your model and tuning your hyperparameters

     This step will take the most time: you’ll repeatedly modify your model, train it, evaluate on your validation data (not the test data, at this point), modify it again, and repeat, until the model is as good as it can get. These are some things you should try:

• Add dropout.
• Try different architectures: add or remove layers.
• Add L1 and/or L2 regularization.
• Try different hyperparameters (such as the number of units per layer or the learning rate of the optimizer) to find the optimal configuration.
• Optionally, iterate on feature engineering: add new features, or remove features that don’t seem to be informative.

     Be mindful of the following: every time you use feedback from your validation process to tune your model, you leak information about the validation process into the model. Repeated just a few times, this is innocuous无害的; but done systematically over many iterations, it will eventually cause your model to overfit to the validation process (even though no model is directly trained on any of the validation data). This makes the evaluation process less reliable.

     Once you’ve developed a satisfactory model configuration, you can train your final production model on all the available data (training and validation) and evaluate it one last time on the test set. If it turns out that performance on the test set is significantly worse than the performance measured on the validation data, this may mean either that your validation procedure wasn’t reliable after all, or that you began overfitting to the validation data while tuning the parameters of the model. In this case, you may want to switch to a more reliable evaluation protocol (such as iterated K-fold validation).

Chapter summary

• Define the problem at hand and the data on which you’ll train. Collect this data, or annotate it with labels if need be.
• Choose how you’ll measure success on your problem. Which metrics will you monitor on your validation data?
• Determine your evaluation protocol: hold-out validation? K-fold validation? Which portion of the data should you use for validation?
• Develop a first model that does better than a basic baseline: a model with statistical power.
• Develop a model that overfits.
• Regularize your model and tune its hyperparameters, based on performance on the validation data. A lot of machine-learning research tends to focus only on this step—but keep the big picture in mind.