「SNOI 2019」积木

传送门

---

problem

有一块 $n$ 行 $m$ 列的网格板，$n,m$ 都是奇数。网格上平铺着一些 $1\times 2$ 的积木。积木可以旋转，不能重叠。这些积木共有 $\frac{nm-1}{2}$ 块，也就是说，网格板上只有一格的空位。

你可以做两种操作：

1. 将一块与空白格相邻（指有公共边）的积木旋转 $90^{\circ }$ 到空白格中；
2. 将一块与空白格积木相邻的积木平移至空白格中。

如图所示（被移动的积木颜色较浅）：

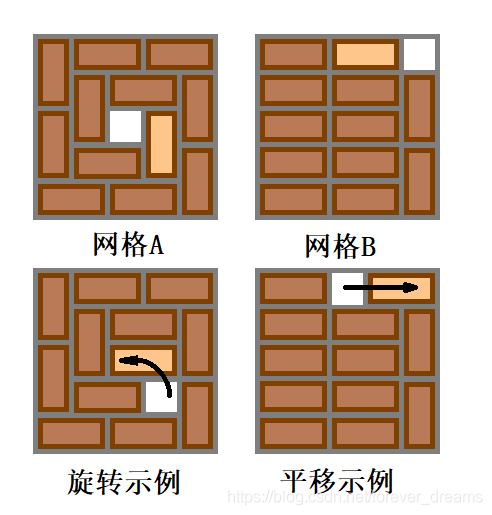
请你用以上两种操作将给定的网格板变换为指定的状态。

数据范围：$1\le n,m\le 2000$。

---

solution

抄参考的神仙博客。

这道题并没有要求操作数最少，只需要求出一个相对较优的操作即可。

考虑其实我们不断让当前空位里该放的牌和结果相同，这样我们显然是找到了一条从初始图里空位到结果图里空位的路径，并且在过去的时候顺便把路径上所有牌摆好了。

存在一个问题，不在这条路径上的位置我们还没有访问过，在这些位置乱掉的牌我们就还没有摆正。

强行把空格子挪过去，然后这个问题就和原问题相同，处理完之后回溯一下即可。

实际上就是在沿路径挪空格的时候，看一下哪个方向的格子是未访问的，把这个方向的连通块处理完之后把空格子挪回来即可。

当然实际上这样也就导致了要访问相同的地方，有一定的无用操作。

另外，代码中有一些很巧妙的细节问题，建议仔细看一看。

---

code

#include
#define N 2005
using namespace std;
int n,m,Sx,Sy,Tx,Ty;
char S[N][N],T[N][N];
bool used[N][N],vis[N][N];
int dx[5]={1,0,-1,0};
int dy[5]={0,1,0,-1};
int way(char c){
	if(c=='n')  return 0;
	if(c=='<')  return 1;
	if(c=='u')  return 2;
	if(c=='>')  return 3;
}
const char *str="n",*op="DRUL";
void go(int d){
	putchar(op[d]);
	int ox=Sx+dx[d],oy=Sy+dy[d];
	int D=way(S[ox][oy]),X=ox+dx[D],Y=oy+dy[D];
	S[X][Y]='o',S[Sx][Sy]=str[d],S[ox][oy]=str[d^2];
	Sx=X,Sy=Y;
}
void Dfs(int x,int y){
	if(vis[x][y]||(x==Tx&&y==Ty))  return;
	int d=way(T[x][y]);
	vis[x][y]=1,x+=dx[d],y+=dy[d],d=way(S[x][y]);
	vis[x][y]=1,x+=dx[d],y+=dy[d],Dfs(x,y);
}
void dfs(int x,int y){
	if(used[x][y])  return;
	used[x][y]=1,Dfs(x,y);
	for(int i=0;i<4;++i){
		int X=x+dx[i],Y=y+dy[i];
		if(X<1||X>n||Y<1||Y>m||vis[X][Y])  continue;
		go(i),dfs(Sx,Sy);
	}
	if(x==Tx&&y==Ty)  return;
	go(way(T[x][y])),dfs(Sx,Sy);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)  scanf("%s",S[i]+1);
	for(int i=1;i<=n;++i)  scanf("%s",T[i]+1);
	for(int i=1;i<=n;++i){
		for(int j=1;j<=m;++j){
			if(S[i][j]=='o')  Sx=i,Sy=j;
			if(T[i][j]=='o')  Tx=i,Ty=j;
		}
	}
	dfs(Sx,Sy);
	return 0;
}