(复习)基础算法--搜索--深入训练(USACO-Feb08、WOW模拟赛Day2-T4、USACO-Dec13、CTSC-1999)
1. USACO-Feb08 流星雨 (meteor.cpp)
题目描述(译文):
贝茜听说了一个骇人听闻的消息:一场流星雨即将袭击整个农场,由于流星体积过大它们无法在撞击到地面前燃烧殆尽,届时将会对它撞到的一切东西造成毁 灭性的打击。很自然地,贝茜开始担心自己的安全问题。以FJ牧场中最聪明的奶牛的名誉起誓,她一定要在被流星砸到前,到达一个安全的地方(也就是说,一块 不会被任何流星砸到的土地)。如果将牧场放入一个直角坐标系中,贝茜现在的位置是原点,并且,贝茜不能踏上一块被流星砸过的土地。
根据预报,一共有M颗流星(1 <= M <= 50,000)会坠落在农场上,其中第i颗流星会在时刻T_i (0 <= T_i <= 1,000)砸在坐标为(X_i, Y_i) (0 <= X_i <= 300;0 <= Y_i <= 300)的格子里。流星的力量会将它所在的格子,以及周围4个相邻的格子都化为焦土,当然贝茜也无法再在这些格子上行走。
贝茜在时刻0开始行动,它只能在第一象限中,平行于坐标轴行动,每1个时刻中,她能移动到相邻的(一般是4个)格子中的任意一个,当然目标格子要没有被烧焦才行。如果一个格子在时刻t被流星撞击或烧焦,那么贝茜只能在t之前的时刻在这个格子里出现。
请你计算一下,贝茜最少需要多少时间才能到达一个安全的格子。
输入格式:
第1行: 1个正整数:M
第2..M+1行: 第i+1行为3个用空格隔开的整数:X_i,Y_i,以及T_i
输出格式:
第1行: 输出1个整数,即贝茜逃生所花的最少时间。如果贝茜无论如何都无法在流星雨中存活下来,输出-1。
思路:
一道很水的BFS,需要注意的只有代码中对地图的预处理部分。用Map数组存储单元格[i][j]在Map[i][j]之后即为不安全的单元格(不能通过的单元格),暴搜即可通过。
代码:
/*
2016.9.20 BulaBulaCHN
*/
#include2.WOW模拟赛 Day2-T4 潜入辛迪加 (syndicate.cpp)
题目描述:
“我们最新的研究成果《毒药研究方案》被可恶的辛迪加偷走了!”作为拉文霍德的一员,你一定感到很震惊,因为它是我们最尖端的科研人员的一年的研究成果。被辛迪加获得,我们可能会有灭顶之灾。
狡猾的辛迪加为了躲避我们的追杀,他们并没有把《毒药研究方 案》带回激流堡,而是把它藏了起来。但是终究是我们技高一筹,运用侏儒的最新研究成果“静电放射探测器”,我们已经发现了他们的藏身之地。原来他们早就在 奥特兰克山脉的地下修建了一个巨大的城市,现在,他们就把《毒药研究方案》放在了城市的最深处。更好的消息是,我们已经发现了地下城的入口。
作为一名出色的盗贼,你要学会以彼之道,还施彼身——把《毒药研究方案》偷回来。然而辛迪加布置了严密的防御,更糟糕的是,他们从地精购买了电磁监视器。无论你的潜行技巧有多么高明,只要一接近它,就会出发警报。只有破坏它的供电系统,才能电磁监视器悄无声息得失效。
现在,“静电放射探测器”已经为我们生成了一张地图,它可以告诉你整个地下城的布局结构,包括每一个电磁监视器的位置,及其供电装置的位置。辛迪加的地下城可以被描述为一个N*N的表格,城市的入口在(1,1)处,目标《毒药研究方案》在(N,N)处。每个单元格可能是一片空地、一个障碍物、一个辛迪加卫士、一个电磁监视器、或者一个的供电装置。
从入口处开始,每步你只能上、下、左、右移动到相邻的一个单元 格,不可以停留在原地。你只能进入空地,或者失去供电系统的电磁监视器的位置,或者摧毁供电装置。你不能移动到障碍物上,也不能进入辛迪加卫士的视线中。 辛迪加卫士可以监视自己所在单元格以及上下左右共五格的位置,而且他们的视线可以重叠。你不能杀死辛迪加卫士,也不能被他们发现。每个电磁监视器的供电装 置可能存在,也可能无法破坏或者根本不存在。一个供电装置也可能会对应零个、一个或多个电磁监视器,意味着摧毁它,对应的所有电磁监视器都会失效。(1,1)和(N,N)一定是可以通行的。
拉文霍德要求你在执行任务之前首先给出一个计划书,即要求算出至少一共需要多少步,才能拿到我们的《毒药研究方案》。
输入格式 :
第1行,两个整数N, M。表示地图大小为N*N,供电装置的数量为M。
第2-N+1行,每行N个整数,每个整数i可能是0,-1,-2或者一个正整数。i=0表示该位置为一块空地,i=-1表示该位置为一个障碍物,i=-2表示该位置为一个辛迪加卫士。如果i是一个属于[1,M]的正整数,则表示该位置为一个供电装置,其编号为i。如果i是一个大于M的正整数,则表示该位置为一个电磁监视器,它的电力由编号为i-M的供电装置提供。
输出格式 :
一个整数,为拿到《毒药研究方案》所需的最少的步数。如果不能到达输出-1.
思路:
一道典型的分层BFS,既把每种持有钥匙的状态转化为一个01串进行存储。运用位运算进行状态转移,仍然是一道很水的题。但是这道题要注意的细节还有一些可说之处:1.你可以穿过供电装置(既存在于供电装置所在的单元格上);2.供电装置有可能和障碍物相重合(此时是否可以穿过供电装置请详细分析样例);3.供电装置有可能和守卫的视线相重合(此时又是否可以穿过供电装置还得详细分析样例)。
代码:
/*
2016.9.20 BulaBulaCHN
*/
#include3.USACO-Dec13 虫洞(wormhole.cpp)
题目描述(译文):
农夫约翰在周末进行高能物理实验的爱好适得其反,导致他的农场中有N个虫洞(2 <= n <= 12),每一个位于在二维地图的不同点。根据他的计算,农民约翰知道他的虫洞有N/2个连接对。
例如,如果A和B是连接虫洞的连接对,那么任何进入虫洞A的物体将从虫洞B退出,任何物体进入虫洞B将同样从虫洞A退出。这可以有相当令人不快的后果。例如,假设有两个配对,虫洞在A(0,0)和B(1,0),而贝茜奶牛从位置(1/2,0)在+X方向移动。她将进入虫洞B,从虫洞A退出,然后再进入B,等等,被困在一个无限循环周期中!
农民约翰知道在他的农场里每一个虫洞的确切位置。他还知道贝茜奶牛总是走在+X方向,但是他不记得贝茜奶牛在哪里,即她现在的位置。请帮助农民约翰计算不同的虫洞配对的数目,满足如果她从一个倒霉的位置开始,她可能会被困在一个无限循环中。
输入格式:
第1行:虫洞的数量,N。
第2..1+N行:每行包含两个整数,描述(x,y),一个单一的虫洞坐标。每个坐标的范围是0..1000000000。
输出格式:
行1:独特的虫洞配对的数目
她可以呆在一个循环周期中,在任意的出发点出发,在+X方向移动。
思路:
这道题的思路就是……妈哒根本没有思路!其实这道题就是一个纯粹的裸DFS而已因为数据范围实在太小,每一层DFS枚举出一对虫洞,最后进行验证即可。
代码:
/*
2016.9.20 BulaBulaCHN
*/
#includereturn a.yint cnt=0;
int ans=0;
bool u[13];
int b[13];
void check()
{
bool flag=0;
for(int i=1;i<=n;i++)
{
int x=i;
for(int j=1;j<=n;j++)
{
int ano=(x%2)?b[x+1]:b[x-1];
if(ano==n || v[ano+1].y!=v[ano].y) break;
for(int k=1;k<=n;k++)
{
if(b[k]==ano+1)
{
x=k;
break;
}
}
if(j==n) {ans++; flag=1; break;}
}
if(flag) break;
}
}
void dfs()
{
if(cnt==n) {check(); return;}
int pos=0;
for(int i=1;i<=n;i++) if(!u[i])
{
b[++cnt]=i;
u[i]=1;
pos=i;
break;
}
for(int i=pos+1;i<=n;i++) if(!u[i])
{
b[++cnt]=i;
u[i]=1;
dfs();
cnt--;
u[i]=0;
}
u[pos]=0;
cnt--;
}
int main()
{
freopen("wormhole.in","r",stdin);
freopen("wormhole.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i].x,&v[i].y);
sort(v+1,v+1+n,cmp);
dfs();
printf("%d",ans);
fclose(stdin);
fclose(stdout);
return 0;
}
4.CTSC-1999 拯救大兵瑞恩(孤岛营救)(rescue.cpp)
题目描述:
1944年,特种兵麦克接到国防部的命令,要求立即赶赴太平洋上的一个孤岛,营救被敌军俘虏的大兵瑞恩。瑞恩被关押在一个迷宫里,迷宫地形复杂,但是幸好麦克得到了迷宫的地形图。
迷宫的外形是一个长方形,其在南北方向被划分为N行,在东西方向被划分为M列,于是整个迷宫被划分为N*M个单元。我们用一个有序数对(单元的行号,单元的列号)来表示单元位置。南北或东西方向相邻的两个单元之间可以互通,或者存在一扇锁着的门,又或者存在一堵不可逾越的墙。迷宫中有一些单元存放着钥匙,并且所有的门被分为P类,打开同一类的门的钥匙相同,打开不同类的门的钥匙不同。
大兵瑞恩被关押在迷宫的东南角,即(N,M)单元里,并已经昏迷。迷宫只有一个入口,在西北角,也就是说,麦克可以直接进入(1,1)单元。另外,麦克从一个单元移动到另一个相邻单元的时间为1,拿取所在单元的钥匙的时间以及用钥匙开门的时间忽略不计。
你的任务是帮助麦克以最快的方式抵达瑞恩所在单元,营救大兵瑞恩。
输入格式:
第一行是三个整数,依次表示N,M,P的值;
第二行是一个整数K,表示迷宫中门和墙的总个数;
第I+2行(1<=I<=K),有5个整数,依次为Xi1,Yi1,Xi2,Yi2,Gi:
当Gi>=1时,表示(Xi1,Yi1)单元与(Xi2,Yi2)单元之间有一扇第Gi类的门,当Gi=0时,表示(Xi1,Yi1)单元与(Xi2,Yi2)单元之间有一堵不可逾越的墙;
(其中,|Xi1-Xi2|+|Yi1-Yi2|=1,0<=Gi<=P)
第K+3行是一个整数S,表示迷宫中存放的钥匙总数;
第K+3+E行(1<=E<=S),有3个整数,依次为Xi1,Yi1,Qi:表示第E把钥匙存放在(Xi1,Yi1)单元里,并且第E把钥匙是用来开启第Qi类门的。(其中1<=Qi<=P)
注意:输入数据中同一行各相邻整数之间用一个空格分隔。
输出格式:
输出文件只包含一个整数T,表示麦克营救到大兵瑞恩的最短时间的值,若不存在可行的营救方案则输出-1。
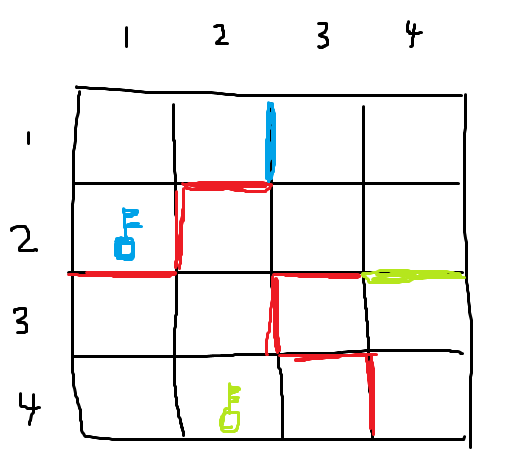
输入样例 :
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
输出样例 :
14
参数设定:
3<=N,M<=15;
1<=P<=10;
思路:
同第二题,这是一道典型的分层DFS,而其状态更小更好储存。但是同样的,作为一道鬼畜的分层BFS试题,它还是有很多鬼畜的细节需要我们去处理!
- 一个单元格中可能有多个钥匙。
- 如果没有样例说明很多人可能看到这道题就想把第二题的码粘过来,但是注意障碍物的存在方式。
- 对于本人代码中这种位置的存储方式会更加方便判断是否可以通行,但是也需要去处理转移状态的细节。
- 小技巧:位运算判断是否能够开门可以利用位运算的按位与操作。
代码:
/*
2016.9.20 BulaBulaCHN
*/
#include最后,需要数据的同学评论留邮。