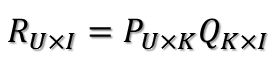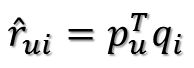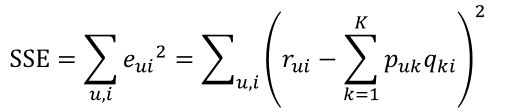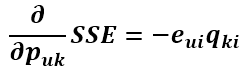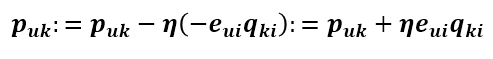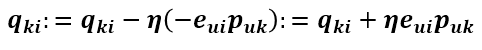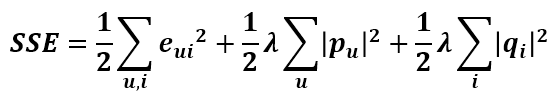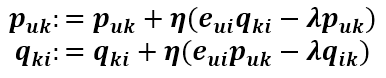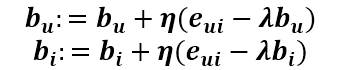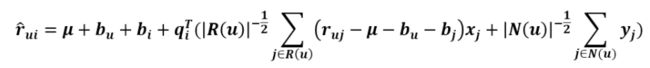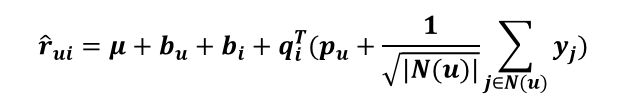理论：SVD及扩展的矩阵分解方法

svd是现在比较常见的算法之一，也是数据挖掘工程师、算法工程师必备的技能之一，这边就来看一下svd的思想，svd的重写，svd的应用。
这边着重的看一下推荐算法中的使用，其实在图片压缩，特征压缩的工程中，svd也有着非常不凡的作用。

svd的思想

1.矩阵因子模型（潜在因子模型）

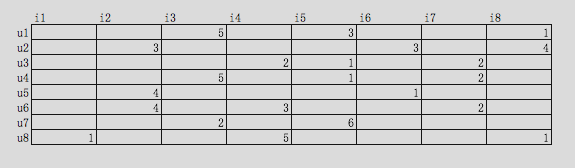
假设，我们现在有一个用户u对商品i的程度矩阵，浏览是1，搜索是2，加车是3，下单是4，付款是5:

用户商品矩阵

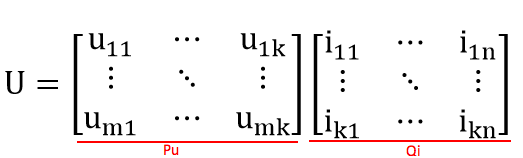
实际情况下，用户不可能什么商品都买，所以，该矩阵必然是一个稀疏矩阵，任意一个矩阵必然可以被分解成2个矩阵的乘积：

k就是潜在因子的个数，举个例子，你去买衣服，你可能买了裙子，露背装，我去买衣服，我买了牛仔裤，潮牌T恤，影响我们购买商品的差异的原因可能有很多点，但是必然有些原因占比重要些，比如性别，收入，有一些可能不那么重要比如天气，心情。而拆分成的Pu矩阵表示了这些潜在因子对我或者你的影响程度，Qi矩阵表示了各种商品对这些潜在因子的影响程度。
当我们尽可能的通过拆分矩阵的形式，目标使得拆分后的两个矩阵的乘积最匹配最上方的用户商品矩阵的已知的数据值，从而可以通过这两个矩阵的乘积填补掉空缺的值。

2.Baseline Predictors

这个是08年的，Koren在NetFlix大赛的一个思路，后续也延伸了svd多种变种，比如Asvd，有偏的Rsvd，对偶算法下的Svd++，这些算法的核心在于解决了Svd上面我们提到的那个矩阵庞大稀疏的问题，后续我们再看。

Baseline Predictors使用向量bi表示电影i的评分相对于平均评分的偏差，向量bu表示用户u做出的评分相对于平均评分的偏差，将平均评分记做μ。

新的得分计算方式如下：Rui＝μ+bi+bu
准备引入了商品及用户的实际分布的情况，有效的降低在测试数据上面的效果。

3.svd数学原理

首先，线代或者高等代数里面告诉我们：一个向量可以通过左乘一个矩阵的方式来进行拉伸，旋转，或者同时拉伸旋转。
所以，无论什么矩阵M，我们都可以找到一组正交基v1、v2，使得Mv1、Mv2也是正交的，不妨记其方向为为μ1、μ2。
Mv1=δ1u1；
Mv2=δ2u2；
存在向量x，在v1、v2空间里的表示为：x=（x·v1）v1+（x·v2）v2，
所以有，Mx有：
Mx=（x·v1）Mv1+（x·v2）Mv2
Mx=（x·v1）δ1u1+（x·v2）δ2u2
Mx=δ1u1(v1.T)x+δ2u2(v2.T)x
M=δ1u1(v1.T)+δ2u2(v2.T)
所以就有了那个非常有名的公式：
M=UΣV.T
U是有一组正交基构成的，V也是有一组正交基构成的，Σ是由δ1、δ2构成的，几何意义上来说，M的作用就是把一个向量由V的正交空间变换到U的正交空间上，而通过Σ的大小来控制缩放的力度。

我们还需要知道一些简单的推论，

• 通过MM.T，我们知道，δ的平方是MM.T的特征值
• 奇异值δ的数量决定了M=UΣV.T的复杂度，而奇异值的大小变化差异程度很大，通常前几个奇异值的平方就能占到全部奇异值的平方的90%，所以，我们可以通过控制奇异值的数量来优化原始矩阵乘积，去除掉一下噪声数据

svd重写

基础的svd

首先，我们在刚开始就知道，评分矩阵R可以用两个矩阵P和Q的乘积来表示：

其中，U表示用户数，I表示商品数，K=就是潜在因子个数。
首先通过那些已知的数据比如下方红色区域内的数据去训练这两个乘积矩阵：

那么未知的评分也就可以用P的某一行乘上Q的某一列得到了：

这是预测用户u对商品i的评分，它等于P矩阵的第u行乘上Q矩阵的第i列。这个是最基本的SVD算法，下面我们们来看如何确定Pu、Qi：

假设已知的评分为：rui则真实值与预测值的误差为：

继而可以计算出总的误差平方和：

只要通过训练把SSE降到最小那么P、Q就能最好地拟合R了。常规的来讲，梯度下降是非常好的求解方式，常见的包括随机梯度下降，批量梯度下降。
随机梯度下降一定程度会避免局部最小但是计算量大，批量梯度计算量小但是会存在鞍点计算误区的问题。

先求得SSE在Puk变量（也就是P矩阵的第u行第k列的值）处的梯度：

现在得到了目标函数在Puk处的梯度了，那么按照梯度下降法，将Puk往负梯度方向变化。令更新的步长（也就是学习速率）为

则Puk的更新式为

同样的方式可得到Qik的更新式为

Rsvd

很明显，上述这样去求的矩阵QP必然会存在过度拟合的问题，导致对实际数据预测的时候，效果远差于训练数据，仿造elastic net的思维：

对所有的变量就加入正则惩罚项，重新计算上面的梯度如下：

这就是正则svd，也叫做Rsvd，也是我们用的比较多的svd的方法。

偏移Rsvd

在最开始讲了，Koren在NetFlix大赛里面除了考虑了对原始数据的拟合情况，也考虑了用户的评分、商品的平均得分相对于整体数据的偏移情况，有了新的得分公式：Rui＝μ+bi+bu，影响的只有eui，后面的Pu、qi的正则不受影响，但是新增了bi、bu的正则项，重新计算每一项的偏导数：
bu、bi的更新式子：

其余的都不发生改变，这就叫做有偏移下的Rsvd

无论是Rsvd还是有偏移的Rsvd，当原始的用户对商品的评分矩阵过大，比如有3亿用户，3亿商品，形成9亿商品集合的时候，这就是一个比较不可能完成的存储任务，而且里面绝大多数都是0的稀疏矩阵。

Asvd及Svd++

这边，我们引入两个集合：R(u)表示用户u评过分的商品集合，N(u)表示用户u浏览过但没有评过分的商品集合，Xj和Yj是商品的属性。
Asvd的rui的评分方式：

Svd++的rui的评分方式：

无论是Asvd还是Svd++，都干掉了原来庞大的P矩阵，取而代之的是两个用户浏览评分矩阵大大缩小了存储的空间，但是随着而来的是一大把更多的未知参数及迭代的复杂程度，所有在训练时间上而言，会大大的增加。

我这边只重写了一下Rsvd的python版本，网上挺多版本的迭代条件有一定问题，稍作处理了一下，并写成了函数，大家可以参考一下：

def svd(mat, feature, steps=2000, gama=0.02, lamda=0.3):  
#feature是潜在因子的数量，mat为评分矩阵
    slowRate = 0.99  
    preRmse = 0.0000000000001
    nowRmse = 0.0 
    
    user_feature = matrix(numpy.random.rand(mat.shape[0], feature))  
    item_feature = matrix(numpy.random.rand(mat.shape[1], feature))  
  
    for step in range(steps):  
        rmse = 0.0    
        n = 0    
        for u in range(mat.shape[0]):  
            for i in range(mat.shape[1]):  
                if not numpy.isnan(mat[u,i]):  
#这边是判断是否为空，也可以改为是否为0:if mat[u,i]>0:
                    pui = float(numpy.dot(user_feature[u,:], item_feature[i,:].T))  
                    eui = mat[u,i] - pui  
                    rmse += pow(eui, 2)  
                    n += 1   
                    for k in range(feature):  
#Rsvd的更新迭代公式
                        user_feature[u,k] += gama*(eui*item_feature[i,k] - lamda*user_feature[u,k])  
                        item_feature[i,k] += gama*(eui*user_feature[u,k] - lamda*item_feature[i,k])
#n次迭代平均误差程度
        nowRmse = sqrt(rmse * 1.0 / n) 
        print 'step: %d      Rmse: %s' % ((step+1), nowRmse)  
        if (nowRmse > preRmse):    
            pass  
        else:  
            break 
#降低迭代的步长
        gama *= slowRate  
        step += 1    
    return user_feature, item_feature  

直接调用的结果如下：

step: 1956      Rmse: 0.782449675844
step: 1957      Rmse: 0.782449675843
step: 1958      Rmse: 0.782449675843
step: 1959      Rmse: 0.782449675843
step: 1960      Rmse: 0.782449675842
step: 1961      Rmse: 0.782449675842
step: 1962      Rmse: 0.782449675842
step: 1963      Rmse: 0.782449675841
step: 1964      Rmse: 0.782449675841
step: 1965      Rmse: 0.78244967584
step: 1966      Rmse: 0.78244967584
step: 1967      Rmse: 0.78244967584
step: 1968      Rmse: 0.782449675839
step: 1969      Rmse: 0.782449675839
step: 1970      Rmse: 0.782449675839
step: 1971      Rmse: 0.782449675838
step: 1972      Rmse: 0.782449675838
step: 1973      Rmse: 0.782449675838
step: 1974      Rmse: 0.782449675837
step: 1975      Rmse: 0.782449675837
step: 1976      Rmse: 0.782449675837
step: 1977      Rmse: 0.782449675836
step: 1978      Rmse: 0.782449675836
step: 1979      Rmse: 0.782449675836
step: 1980      Rmse: 0.782449675835
step: 1981      Rmse: 0.782449675835
step: 1982      Rmse: 0.782449675835
step: 1983      Rmse: 0.782449675835
step: 1984      Rmse: 0.782449675834
step: 1985      Rmse: 0.782449675834
step: 1986      Rmse: 0.782449675834
step: 1987      Rmse: 0.782449675833
step: 1988      Rmse: 0.782449675833
step: 1989      Rmse: 0.782449675833
step: 1990      Rmse: 0.782449675833
step: 1991      Rmse: 0.782449675832
step: 1992      Rmse: 0.782449675832
step: 1993      Rmse: 0.782449675832
step: 1994      Rmse: 0.782449675831
step: 1995      Rmse: 0.782449675831
step: 1996      Rmse: 0.782449675831
step: 1997      Rmse: 0.782449675831
step: 1998      Rmse: 0.78244967583
step: 1999      Rmse: 0.78244967583
step: 2000      Rmse: 0.78244967583
Out[15]: 
(matrix([[-0.72426432,  0.40007415,  1.16887518],
         [-0.73130968,  0.40240702,  1.14708432],
         [ 0.34759923,  1.35065656, -0.29573789],
         [ 1.17462156, -0.04964694,  0.73881335],
         [ 2.04035441, -0.06798676,  1.28078727],
         [ 0.30446306,  1.71648612, -0.4109819 ],
         [ 1.71963828, -0.00833196,  1.25983483],
         [-0.86341514,  0.47750529,  1.36135332],
         [-0.48881234,  0.57942923,  0.77110915],
         [ 0.29282908,  1.5164249 , -0.39811768],
         [ 0.35369432, -0.00964055,  0.22328158]]),
 matrix([[ 1.3381854 , -0.05425608,  0.87036818],
         [ 1.07547853, -0.04515239,  0.69607952],
         [ 1.39038494, -0.05799558,  0.90186332],
         [-0.60218508,  0.36233309,  0.92136536],
         [ 0.39117217,  1.9272062 , -0.50710187],
         [-0.93202395,  0.52982297,  1.43309143],
         [-0.19393338,  0.40429152,  0.29994372],
         [ 1.40108031,  0.06915628,  0.87647945],
         [ 1.39446638, -0.05197355,  0.920216  ],
         [ 0.31981929,  1.84114505, -0.40108819],
         [-0.82317832,  0.52798144,  1.51619052]]))

svd在推荐算法中的使用

数据集中行代表用户user，列代表物品item，其中的值代表用户对物品的打分。
基于SVD的优势在于：用户的评分数据是稀疏矩阵，可以用SVD将原始数据映射到低维空间中，然后计算物品item之间的相似度，更加高效快速。

整体思路：
用户未知得分的商品评分计算方式：
1.用户的评分矩阵==》用户已经评分过得商品的得分
2.商品的用户评分==》用户已经评分过得商品和其他每个商品的相关性
3.“用户已经评分过得商品的得分”*“用户已经评分过得商品和某个未知评分商品的相关系数”=某个未知商品该用户的评分

计算上面三个步骤，我们需要：
1.考虑采取上面相关性的计算方式
2.考虑潜在因子的个数

依旧python代码，我会在代码中注释讲解：
1.首先相关性

# 欧拉距离相似度，评分可用，程度不建议
def oulasim(A, B):
    distince = la.norm(A - B)  # 第二范式：平方的和后求根号
    similarity = 1 / (1 + distince)
    return similarity


# 余弦相似度，评分、1/0、程度都可以用
def cossim(A, B):
    ABDOT = float(dot(A, B))
    ABlen = la.norm(A) * la.norm(B)
    if ABlen == 0:
        similarity = '异常'
    else:
        similarity = ABDOT / float(ABlen)
    return similarity


# 皮尔逊相关系数
def pearsonsim(A, B):
    A = A - mean(A)
    B = B - mean(B)
    ABDOT = float(dot(A, B))
    ABlen = la.norm(A) * la.norm(B)
    if ABlen == 0:
        similarity = '异常'
    else:
        similarity = ABDOT / float(ABlen)
    return similarity

2.指定用户及对应商品的相似度

# svd
def recommender(datamat,user,index,function):
    n = shape(datamat)[1]  # 商品数目
    U, sigma, VT = la.svd(datamat)
    # 规约最小维数
    sigma2 = sigma ** 2
    k = len(sigma2)
    n_sum2 = sum(sigma2)
    nsum = 0
    max_sigma_index = 0
#奇异值的平方占比总数的90%，确定潜在因子数
    for i in sigma:
        nsum = nsum + i ** 2
        max_sigma_index = max_sigma_index + 1
        if nsum >= n_sum2 * 0.9:
            break
    # item new matrix
    item = datamat.T * U[:, 0:max_sigma_index] * matrix(diag(sigma[0:max_sigma_index])).I
    key=item[index,:]
    total_similarity=0
    rank_similarity=0
    for i in range(k):
#如果用户没有评分或者与用户选择想知道的商品一致则跳过，不跳过计算出来前者是得分0，后者直接是用户已评分的结果，没有意义
            if datamat[user,i]==0 or i==index:continue
            similarity=function(key,item[i,:].T)
            total_similarity=total_similarity+similarity
#用户的评分*相关系数
            rank_similarity=rank_similarity+similarity*datamat[user,i]*similarity
    score = rank_similarity/total_similarity
    return score

比如：用户1在商品1的得分为3.99分

In [18]: recommender(data,1,1,cossim)
Out[18]: 3.98921610058786

3.指定商品，与所有其它商品的相似度

def recommender(datamat, item_set, method):
    col = shape(datamat)[1]  # 物品数量
    item = datamat[:, item_set]
    similarity_matrix = zeros([col, 1])
    for i in range(col):
        index = nonzero(logical_and(item > 0, datamat[:, i] > 0))[0]
        if sum(index) > 0:
            similarity = method(datamat[index, item_set].T, datamat[index, i])
        else:
            similarity = '-1'
        similarity_matrix[i] = similarity
    return similarity_matrix

比如：商品0，对其它所有商品的相似度：

In [24]: recommender(data,0,cossim)
Out[24]: 
array([[ 1.        ],
       [ 0.99439606],
       [ 0.99278096],
       [-1.        ],
       [-1.        ],
       [-1.        ],
       [-1.        ],
       [ 0.98183139],
       [ 0.97448865],
       [-1.        ],
       [ 1.        ]])

4.直接算出所有商品间的相似度：

def similarity(datamat, method):
    item_sum = shape(datamat)[1]
    similarity = pd.DataFrame([])
    for i in range(item_sum):
        res = recommender(datamat, i, method)
        similarity = pd.concat([similarity, pd.DataFrame(res)], axis=1)
    return similarity

比如商品的相似矩阵：

In [25]: similarity(data,cossim)
Out[25]: 
           0         0         0         0         0         0         0  \
0   1.000000  0.994396  0.992781 -1.000000 -1.000000 -1.000000 -1.000000   
1   0.994396  1.000000  0.999484 -1.000000 -1.000000 -1.000000 -1.000000   
2   0.992781  0.999484  1.000000 -1.000000 -1.000000 -1.000000 -1.000000   
3  -1.000000 -1.000000 -1.000000  1.000000 -1.000000  0.990375  1.000000   
4  -1.000000 -1.000000 -1.000000 -1.000000  1.000000 -1.000000  1.000000   
5  -1.000000 -1.000000 -1.000000  0.990375 -1.000000  1.000000  1.000000   
6  -1.000000 -1.000000 -1.000000  1.000000  1.000000  1.000000  1.000000   
7   0.981831  0.956858  0.955304 -1.000000  1.000000 -1.000000 -1.000000   
8   0.974489  0.956858  0.955304 -1.000000 -1.000000 -1.000000 -1.000000   
9  -1.000000 -1.000000 -1.000000  1.000000  0.994536  1.000000  0.384615   
10  1.000000  1.000000  1.000000  1.000000 -1.000000  0.981307  1.000000   

           0         0         0         0  
0   0.981831  0.974489 -1.000000  1.000000  
1   0.956858  0.956858 -1.000000  1.000000  
2   0.955304  0.955304 -1.000000  1.000000  
3  -1.000000 -1.000000  1.000000  1.000000  
4   1.000000 -1.000000  0.994536 -1.000000  
5  -1.000000 -1.000000  1.000000  0.981307  
6  -1.000000 -1.000000  0.384615  1.000000  
7   1.000000  0.991500  1.000000  1.000000  
8   0.991500  1.000000 -1.000000  1.000000  
9   1.000000 -1.000000  1.000000  1.000000  
10  1.000000  1.000000  1.000000  1.000000  

5.指定用户下的top5商品推荐

def fianl_recommender(datamat,user,function):
    unratedItems=nonzero(datamat[user,:].A==0)[1]
    if len(unratedItems)==0: print 'ok'
    score=[]
    for i in unratedItems:
        i_score=recommender(datamat,user,i,function)
        score.append((i,i_score))
    score=sorted(score,key=lambda x:x[1],reverse=True)
    return score[:5]

比如指定用户1，最适合推荐的商品如下：

In [31]: fianl_recommender(data,1,pearsonsim)
Out[31]: 
[(7, 3.3356853252871588),
 (8, 3.3349455396520296),
 (0, 3.33492840157654),
 (2, 3.334920725716121),
 (1, 3.334919898261294)]

最后，谢谢大家阅读。

---

欢迎大家关注我的个人bolg，更多代码内容欢迎follow我的个人Github，如果有任何算法、代码疑问都欢迎通过公众号发消息给我哦。

少年，扫一下嘛