一个特别有意思的算法——多边形游戏

世界上有许许多多的不可能,但是即使再不可能。合全人类的力量还能做不成吗
地球本身就是一个大的自然圈。而这些用具、房屋、衣物不都是人类一点点装饰起来的
我认为从无到有是最困难的事情。然而文明、科技、器械等一代代创建和传承。
所以我们面对困难不要轻言放弃，哪怕用自己的想法证明这是一件我做不到、就是一件困难的事情，也要按照这个想法做一遍。

本篇介绍一个多边形游戏算法，它也是一个动态规划的经典算法。

1、多边形游戏算法

什么是多边形游戏算法

给定N个顶点的多边形，每个顶点标有一个整数，每条边上标有+(加)或是×(乘)号，并且N条边按照顺时针
依次编号为1~N。下图给出了一个N＝4个顶点的多边形。

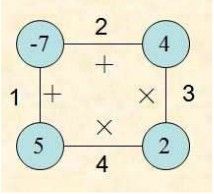
游戏规则 ：(1) 首先，移走一条边。 (2) 然后进行下面的操作： 选中一条边E，该边有两个相邻的顶点，不妨称为V1和V2。对V1和V2顶点所标的整数按照E上所标运算符号(+或是×)进行运算，得到一个整数；用该整数标注一个新顶点，该顶点代替V1和V2 。 持续进行此操作，直到最后没有边存在，即只剩下一个顶点。该顶点的整数称为此次游戏的得分(Score)。

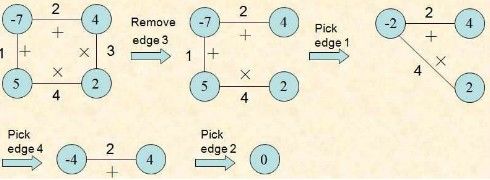
动态规划算法解多边形游戏问题

设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],op[3],…,op[n],v[n] 其中，op[i]表示第i条边所对应的运算符，v[i]表示第i个顶点上的数值，i=1~n。

在所给的多边形中，从顶点i（1<=i<=n）开始，长度为j（链中有j个顶点）的顺时针链p(i,j）可表示为v[i],op[i+1],…,v[i+j-1]，如果这条链的最后一次合并运算在op[i+s]处发生（1<=s<=j-1），则可在op[i+s]处将链分割为两个子链p(i,s)和p(i+s,j-s)。

设m[i,j,0]是链p(i,j)合并的最小值，而m[i,j,1]是最大值。若最优合并在op[i+s]处将p(i,j)分为两个长度小于j的子链的最大值和最小值均已计算出。即：
　　 a=m[i,s,0] b=m[i,s,1] c=m[i,s,0] d=m[i,s,1]
　　(1) 当op[i+s]=’+’时
　　　　m[i,j,0]=a+c ；m[i,j,1]=b+d
　　 (2) 当op[i+s]=’*’时
　　　　 m[i,j,0]=min{ac,ad,bc,bd} ； m[i,j,1]=max{ac,ad,bc,bd}

由于最优断开位置s有1<=s<=j-1的j-1中情况。 初始边界值为 m[i,1,0]=v[i] 1<=i<=n m[i,1,1]=v[i] 1<=i<=n

综上可知多边形游戏问题满足最优子结构性质

设m[i,j,0]是链p(i,j)的最小值，而m[i,j,0]是链p(i,j)的最大值。若最优合并在op[i+s]处将p(i,j)分为长度小于j的子链p(i,i+s)和p(i+s,i-s)。然后我们计算最值
a=m[i,i+s,0]
b=m[i,i+s,1]
c=m[i+s,j-s,0]
d=m[i+s,j-s,1]

然后去计算加和乘法得到最值，然后进行比较。因为最优断开位置s有1<=s<=j-1的j-1种情况，由此可知
m[i,1,0]=v[i]   1<=i<=n
m[i,1,1]=v[i]   1<=i<=n

由于多边形是封闭的，在上面的计算中，当i+s>n时，我们就得去用到数据结构上的环链结构：
(i+s-1)%n+1

最后的m[i,n,1]就是问题的最高分

我们看上面的那个例子：
输入n个端点，n个符号
输出在断掉第i条边后得到最高分maxscore，请将i,maxscore输出
我们先将四个点的值作为初值记录备忘录里；

然后计算两个点，将-7+4，4·2，2·(-5)，5+(-7)，记到备忘录里。

然后计算三个点，-7与4先运算再和2运算或者-7在4和2运算完，-7再与它们直接的结果进行运算。由于运算之间是两点运算后再与另一个点进行计算。然而两点运算是保存在了备忘录里了。最后两点运算后的结果和另外一个点要进入运算方法进行计算的，找到最值返回的。

同理4要先和2进行运算再和5进行运算得到值m1。或者是4在2和5运算完，4再与它们的结果进行运算得到的值m2。
然后比较m1和m2的大小关系（包括最小值和最大值），找到一个真正的最小值和最大值。

大家应该能看到，顺时针输入数据和符号。也是顺时针计算和求解

当初我再接触这个的时候，我总觉得书上和网上的介绍有错误。前面的算法是可以的。我觉得最后的求解是有问题的。书上的地方说的是m[i,n,1]是断掉第i条边后的最大值。实则经过我测试，我觉得是m[i,n,1]中if(i==1)P=n;else P=i-1;应该是这种情况才对。因为经过我分析代码的时候，无论从哪一个点开始顺时针计算，这个点逆时针的第一条边是没有被算进去的。也就是要被断的边。

对于代码分析：我们知道这个数组是一个三维数组，而且j是涵盖的点的个数。i是第几个点，s是划分。
我们这里只分析循环下标
这里令一个点的情况我们在进入方法前，就已经赋值完了。那么从第二点开始计算。
总共有n个点
对于s，上边也说了s从1取到j-1。
所以遍历下标就是这样的：
j=2,j<=n,j++
i=1,i<=n;i++
s=1,s

接下来我们直接上代码：

public static int minf;  //最小值
	public static int maxf;  //最大值
	public static int P;  //删减点
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner scanner=new Scanner(System.in);
		System.out.println("请输入多边形顶点数：");
		int N=scanner.nextInt();
		char op[]=new char[N+1];  //存放运算符
		int m[][][]=new int[N+1][N+1][2];
		for(int i=1;i<=N;i++) {
			System.out.println("请输入第"+i+"个顶点的数值：");
			m[i][1][0]=scanner.nextInt();
			m[i][1][1]=m[i][1][0];
			System.out.println("请输入第"+i+"个运算符：");
			op[i]=scanner.next().charAt(0);
		}
		int maxscore=PolydonmaxScore(N, m, op);
		System.out.println("首次删减第"+P+"个边");
		System.out.println("最大得分是："+maxscore);
		
	}
	
	//动态规划解多边形游戏
	public static int PolydonmaxScore(int N,int m[][][],char op[]) {
		for(int j=2;j<=N;j++)
			for(int i=1;i<=N;i++)
				for(int s=1;s<j;s++) {
					MaxMin(N, i, s, j, m, op);
					if(m[i][j][0]>minf)
						m[i][j][0]=minf;
					if(m[i][j][1]<maxf)
						m[i][j][1]=maxf;
				}
		
		int temp=m[1][N][1];
		P=N;
		
		for(int i=2;i<=N;i++)
			if(temp<m[i][N][1]) {
				temp=m[i][N][1];
				P=i-1;
			}
		
		return temp;
	}
	
	//求最小和最大分
	public static void MaxMin(int N,int i,int s,int j,int m[][][],char op[]) {
		int e[]=new int[5];
		int a=m[i][s][0],b=m[i][s][1];
		int r=(i+s-1)%N+1;  //下一个多边形的实际顶点编号,冗余设计为了防止(1+3)%4为0的情况
		int c=m[r][j-s][0],d=m[r][j-s][1];
		if(r-1==0)
			r=N+1;
		if(op[r-1]=='+') {
			minf=a+c;
			maxf=b+d;
		}else {
			e[1]=a*c;
			e[2]=a*d;
			e[3]=b*c;
			e[4]=b*d;
			minf=e[1];
			maxf=e[1];
			
			for(int k=2;k<=4;k++) {
				if(minf>e[k])
					minf=e[k];
				if(maxf<e[k])
					maxf=e[k];
			}
		}
	}

最后分析下时间复杂度

动态规划算法解多边形游戏分析

我们看到了，这里有三层循环，所以很自然的能看到时间复杂度就是O(n^3)

而追踪解只有一层循环，就是那个求最大值和断点的代码那里
则时间复杂度就是O(n)

综上动态规划算法解多边形游戏的时间复杂度就是O(n^3)

以上就是动态规划算法解多边形游戏问题的内容

2、动态规划算法总结

动态规划算法设计要点

1、引入参数来界定子问题的边界，注意子问题的重叠程度

####2、给出带边界参数的优化函数定义与优化函数的递推关系，找到递推关系的初值
####3、判断该优化问题是否满足优化原则
####4、考虑是否需要标记函数
####5、采用自底向上的实现技术，从最小子问题开始迭代计算，计算中用备忘录保留优化函数和标记函数的值。要将表设计好
####6、对于时间复杂度分析：
####所有子问题的计算工作量+追踪解的工作量
####7、动态规划算法一般使用较多的存储空间，这往往成为限制动态规划算法使用的瓶颈因素

动态规划算法的好处就是空间换时间，每个子问题只计算一次，从而得到更好的效率。

动态规划算法代码设计

关于代码如何编写。我觉得得先想清楚算法策略，得出的递推方程是否满足依赖关系。然后可以根据这个递推方程来编写代码。

首先建立一个表，这个表可能是一维数组、也可能是二维数组。
然后根据问题设计，编写主要代码块。
一遍是把最小子问题（记住：先从最小子问题开始入手，不然就有可能子问题会被计算多次）放到前面先计算。然后开始for循环迭代你所设计的递推方程内容。所以说数学有助于代码设计和编写

追踪解：
我们首先考虑清楚是否要标记函数，不考虑那就在得出最值的时候直接求解就行（如：多边形游戏）。需要标记函数，那就建一个一维或者二维的数组来记录解。最后通过设计一个追踪解的方法来自底向上（记住：一定是自底向上）求出解

动态规划算法在做算法题中很常见。多学多练才是硬道理。

         天行健，君子以自强不息；地势坤，君子以厚德载物 《周易》