算法基础：狄克斯特拉算法（基于Python）

本博客所有内容均整理自《算法图解》，欢迎讨论交流~

之前在引入图算法和广度优先搜索的时候，我举了一个旅行最短距离的例子，其实在那一节，广度优先搜索并没有解决那个例子的问题，在这里使用狄克斯特拉算法才可以真正解决赋权图的最短距离问题。

我们依然沿用那个例子。

假设你要从北京到成都去旅游，但是已经买不到北京直达成都的火车票或者飞机票了，于是你决定中转。现在有以下几种中转方案：

1、北京-乌鲁木齐-西安-成都

2、北京-合肥-武汉-成都

3、北京-大连-上海-重庆-成都

4、北京-九江-广州-昆明-成都

我们不考虑价格，仅仅考虑距离，这几种方案哪个距离最短呢？

其实这里我们首先要弄清楚的是，在这几种方案中，每两个城市之间的距离是多少。有了这些距离之后，我们才可以画出每种方案的图，把这些距离标在两个城市之间的连线上。这种边带有权值的图称为赋权图。

找到赋权图中前往X的最短路径，我们常使用狄克斯特拉算法。

---

1、狄克斯特拉算法的基本概念

关于狄克斯特拉算法的定义，百度百科是这样给出的：狄克斯特拉算法是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。狄克斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

下面来看看如何对下面的图使用这种算法。

 

对于上面的图，每条边都有一个权值，在这里代表从有向边的起点到终点所需的时间。如果我们需要找出从起点到达终点的最短路径，就可以使用狄克斯特拉算法来解决这个问题。

在使用狄克斯特拉之前，我们先来看看使用广度优先搜索算法来解决这个问题的结果，如下图所示：

上图中较粗的那一条路径，是使用广度优先搜索算法获得的最短路径，因为该路径只有两段，经过的节点最少，所以广度优先搜索把该路径认定为最短路径，因为广度优先搜索算法只考虑经过的节点最少，不考虑边的权值。

这条路径耗时7分钟，下面来看看使用狄克斯特拉算法能否找到耗时更短的路径！

狄克斯特拉算法算法主要包含四个步骤：

1. 找出“最近”的节点，即在最短时间内可到达的节点。
2. 更新该节点的邻居的开销。
3. 重复这个过程，直到对图中的所有节点都执行过该操作。
4. 计算最终路径。

第一步：START，找到最近的节点

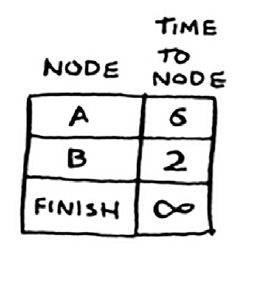
最开始，我们处于点START，此时我们可以前往A点和B点，前往A点需要6个单位时间，前往B点需要2个单位时间。至于其他的节点，此时我们并不知道需要多少单位时间可到达，所以暂时假设为无穷大单位时间。

由于狄克斯特拉算法在第一步是找出“最近”的可在最短时间内到达的节点，所以在此时，我们选择B节点。

第二步：B，更新邻居节点开销

此时我们处于节点B。于是我们首先计算B节点的邻居的距离开销，然后更新各节点的开销。

B节点前往A节点需要3个单位时间，前往终点需要5个单位时间。由于起点到达B节点还需要2个单位时间，所以总时间分别为2+3=5个单位时间和2+5=7个单位时间。

因此开销表更新为：
 

因此我们找到了一条前往A节点的更近的路径！

第三步：重复！

此时我们开始重复。

重复第一步：找出最近的节点。在第一步时，我们选择了节点B，已经更新了节点B的所有邻居的开销，所以除节点B外，最近的节点就是节点A了。

重复第二步：更新节点A的所有邻居的开销。由于A点前往终点的开销为1个单位时间，所以加上前往节点A的开销，总开销为5+1=6个单位时间！

所以开销表再一次更新：

第四步：计算最终路径

此时我们已经对所有节点都进行了邻居开销的更新了。

所以，我们此时可以来计算最终路径了。根据开销表，前往终点的最短路径的距离为6个单位时间。

最短路径为START->B->A->FINISH。

看完了前面的完整四个步骤，我想大家应该也都发现了，要想使用狄克斯特拉算法，一定得是有向无环图！而且权值必须是正数！因为如果是无向图，则权值是双向的，就很可能导致两个节点互相最近，于是就在两个节点之间无限循环！而有环是同样的道理，一旦有环了，就有可能陷入循环中！

---

2、狄克斯特拉算法的代码实现

我们依然以下图为例：

 

编写该问题的代码，我们需要三个散列表：
 

 

随着算法的进行，你将不断地更新散列表costs和parents。

首先，我们要思考这样一个问题：我们如何用代码表示costs散列表呢？其实，我们使用双散列表即可，类似于二维数组：

graph = {}

graph["start"]["a"] = 6

graph["start"]["b"] = 2

因此graph["start"]是一个散列表，可以使用graph["start"].keys()来获取起点的所有邻居节点。

下面来添加其他节点及其邻居节点：

graph["a"] = {}

graph["a"]["fin"] = 1

 

graph["b"] = {}

graph["b"]["a"] = 3

graph["b"]["fin"] = 5

 

graph["fin} = {}

于是整个图的散列表如下所示：

 

其中，start,a,b,fin也都是一个散列表。

接下来我们以相同的道理来创建存储开销和存储父节点的散列表。这里存储父节点，是为了最终获得最短路径，因为如果没有存储每一步的父节点，我们在终点就不知道如何回到起点了。

最后，我们还需要一个数组来存储已经处理过的节点。

所以，实现狄克斯特拉算法的Python代码如下所示：

graph = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

graph["a"] = {}
graph["a"]["fin"] = 1

graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5

graph["fin} = {}

infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node

node = find_lowest_cost_node(costs)
while node is not None:
    cost = costs[node]
    neighbors = graph[none]
    for n in neighbors.keys():
        new_cost = cost + neighbors[n]
        if costs[n] > new_cost:
            costs[n] = new_cost
            parents[n] = node
    processed.append(node)
    node = find_lowest_cost_node(costs)

最终，我们从终点回溯。首先通过parents["fin"]可以得到节点A，然后从parents["a"]可以得到节点B，接着从parents["b"]可以得到起点START。所以，最优路径为START->B->A->FIN。