数据结构之二分搜索树

二分搜索树

什么是树？

树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。

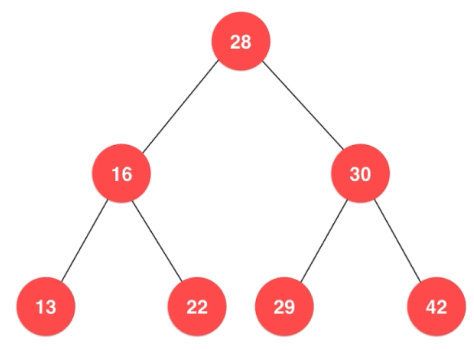
二分搜索树的每一个节点的值都大于左子树的所有节点的值，同时小于其右子树的所有节点的值，每一颗子树都是一颗二分搜索树。

需要注意的是二分搜索树并不一定每个节点都有子节点，并且存储的元素必须有可比较值。

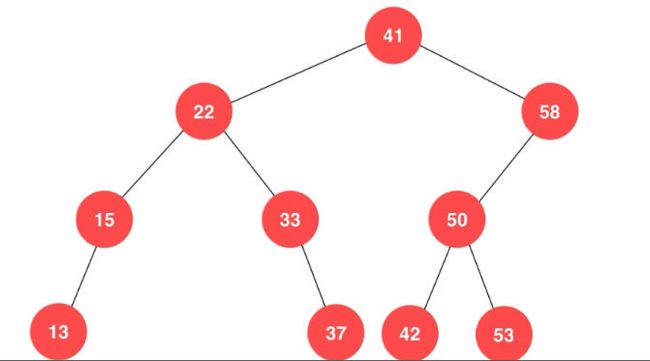
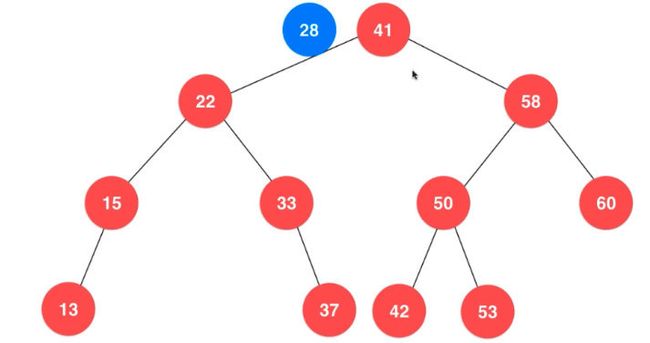
向二分搜索树添加元素

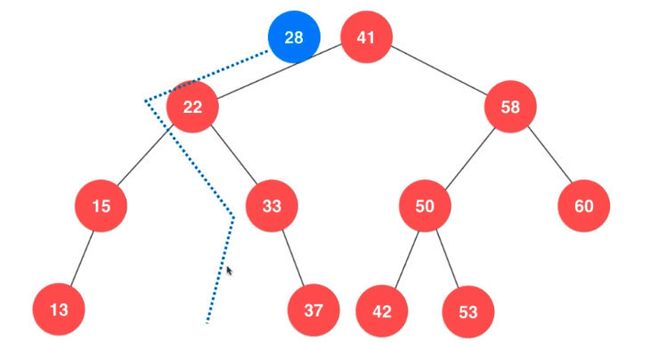
如上图所示，我们如果想插入28元素，我们需要判断插入在根节点的左孩子还是右孩子，28比41小，所以要插入在左孩子里，然后比较22，发现比22大所以要比较22的右孩子，然后比较33，发现比33小所以就比较33的左孩子，但是发现33没有左孩子了，这个时候我们就可以将28插入在33的左孩子位置。

使用递归实现添加操作

public class BST> {
        private class Node {
            private E e;
            //定义左节点和右节点
            private Node left, right;
            public Node(E e) {
                this.e = e;
                left = null;
                right = null;
            }
        }
        private Node root;
        private int size;
        public int size() {
            return size;
        }
        public boolean isEmpty() {
            return size == 0;
        }
        public void add(E e) {
            root = add(root, e);
        }
        //向以node为根的二分搜索树中插入元素E，递归算法
        private Node add(Node node, E e) {
            if (node == null) {
                size++;
                return new Node(e);
            }
            if (e.compareTo(node.e) < 0) {
                node.left = add(node.left, e);
            } else if (e.compareTo(node.e) > 0) {
                node.right = add(node.right, e);
            }
            return node;
        }
}

二分搜索树查询元素

具体实现逻辑和添加类似，都是使用递归来实现。

    public boolean contains(E e){
        return contains(root,e);
    }
    private boolean contains(Node node,E e){
        if (node == null){
            return false;
        }
        if (e.compareTo(node.e) < 0) {
            return contains(node.left, e);
        } else if (e.compareTo(node.e) > 0) {
            return contains(node.right, e);
        }
        return true;
    }

二分搜索树的前序遍历

先访问这个节点，再访问这个节点的左子树，最后访问这个节点的右子树，这就是前序遍历。

对于遍历操作，两颗子树都要顾及。

    //二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }
    //前序遍历以node为根的二分搜索树，递归算法
    private void preOrder(Node node){
        if (node == null) {
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

二分搜索树的中序遍历

先访问这个节点左子树，再访问这个节点，最后访问这个节点的右子树，这就是中序遍历。

打印输出的结果是排序好的数据。

    //中序遍历
    public void inOrder(){
        inOrder(root);
    }
    //中序遍历以node为根的二分搜索树，递归算法
    private void inOrder(Node node){
        if (node == null) {
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

二分搜索树的后序遍历

先访问这个节点左子树，再访问这个节点的右子树，最后访问这个节点，这就是后序遍历。

    //后序遍历
    public void postOrder(){
        postOrder(root);
    }
    //后序遍历以node为根的二分搜索树，递归算法
    private void postOrder(Node node){
        if (node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

二分搜索树的层序遍历

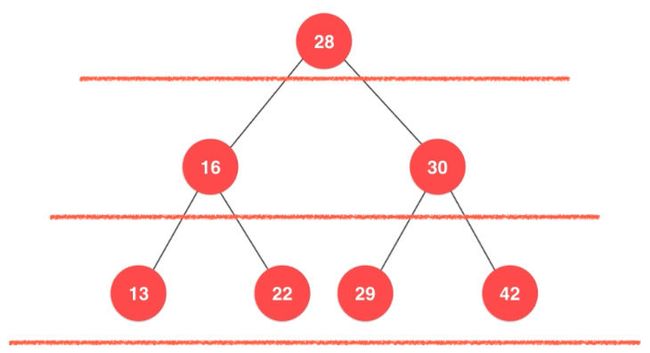
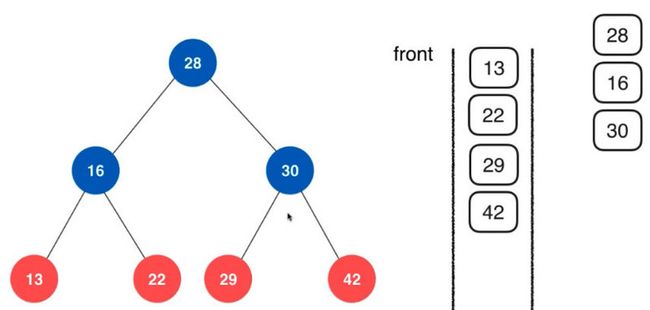
层序遍历其实就是广度优先遍历。

我们可以借助队列来实现层序遍历。

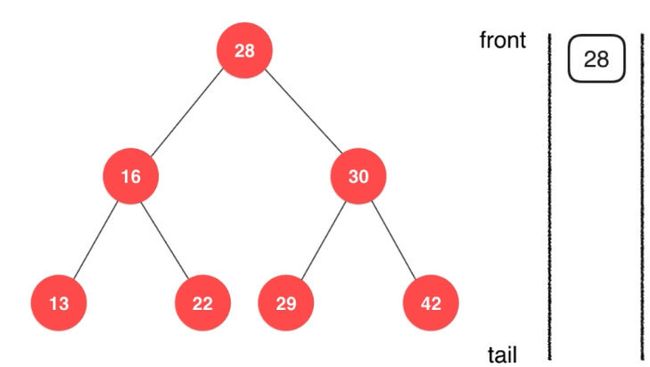
在一开始的时候我们将根节点放入队列中。然后访问28来进行操作。

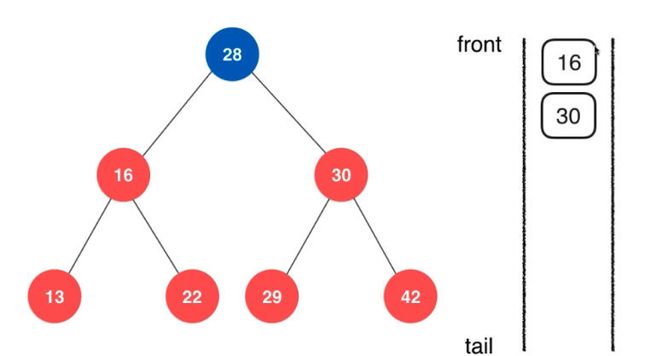
之后我们将28的左右两个孩子分别入队，之后进行操作。

然后访问16和30，将16的左右孩子和30的左右孩子放入队列。

public void levelOrder(){
        Queue queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            Node cur = queue.remove();
            System.out.println(cur.e);
            if (cur.left != null){
                queue.add(cur.left);
            }
            if (cur.right != null){
                queue.add(cur.right);
            }
        }
}

删除最大和最小元素

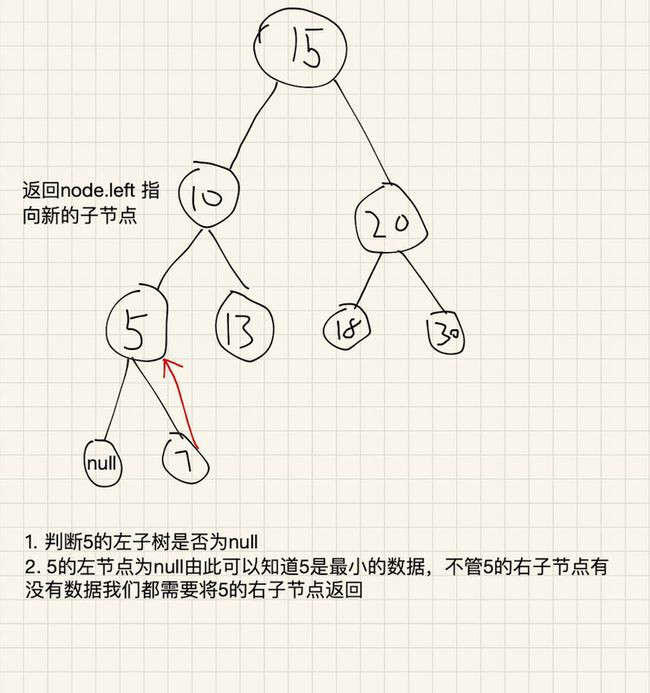
删除最小元素的基本逻辑为，先获取到最小元素，然后调用删除函数，从根节点出发递归查询左子树是否为null，如果为null则将右子树返回到node的左子树上。不管右子树是否为null都可以返回到左子树。删除最大元素同理。

    //寻找二分搜索树的最小元素
    public E minimum() {
        if (size == 0) {
            return null;
        }
        return minimum(root).e;
    }
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }
    //寻找二分搜索树的最大元素
    public E maximum() {
        if (size == 0) {
            return null;
        }
        return maximum(root).e;
    }
    private Node maximum(Node node) {
        if (node.right == null) {
            return node;
        }
        return maximum(node.right);
    }
    //二分搜索树中删除最小值的元素，返回最小值
    public E removeMin() {
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }
    private Node removeMin(Node node) {
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }
    //二分搜索树中删除最大值的元素，返回最大值
    public E removeMax() {
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }
    private Node removeMax(Node node) {
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }
        node.right = removeMax(node.right);
        return node;
    }

二分搜索树删除任意节点

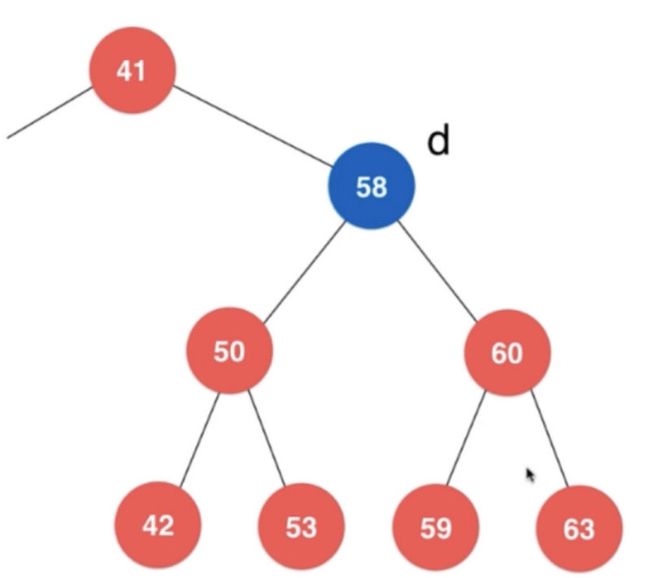
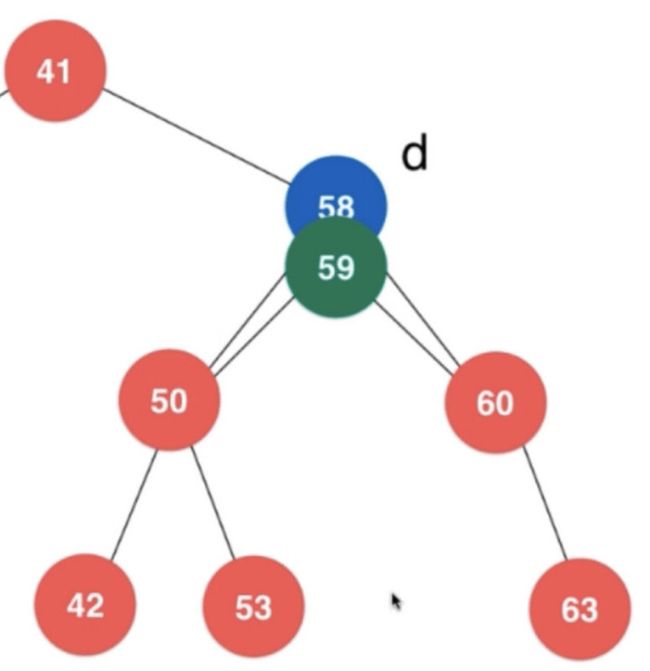
如果我们要删除58节点，我们需要从58的子节点中获取到比58大并且离58最近的一个节点来当新的节点。

也就是58的右节点中的最左根节点就是满足我们条件的值。

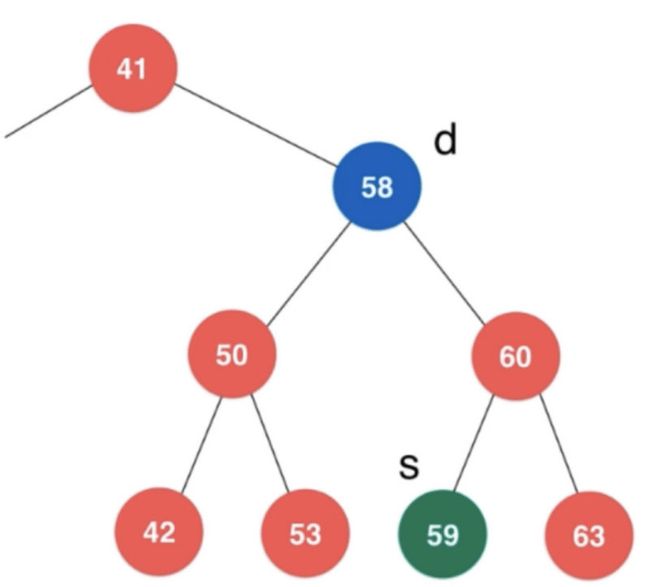
我们需要删除S节点，然后将S节点移动到D节点。然后将D节点的左右子节点赋给S节点，最后删除D节点。

    //从二分搜索树中删除为e的节点
    public void remove(E e) {
        root = remove(root, e);
    }
    private Node remove(Node node, E e) {
        if (node == null) {
            return null;
        }
        if (e.compareTo(node.e) < 0) {
            node.left = remove(node.left, e);
            return node;
        } else if (e.compareTo(node.e) > 0) {
            node.right = remove(node.right, e);
            return node;
        }else{
            //待删除的左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size--;
                return rightNode;
            }
            //待删除的右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size--;
                return leftNode;
            }
            //待删除的节点左右子树均不为空的情况
            //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
            //用这个节点代替删除的节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;
            node.left = node.right = null;
            return successor;
        }
    }