树结构大全

说明

---

• 主要讲解二叉树及其相关内容
• 次要说明其他树结构
• 以后会进行不定期更新

主要参考以下书籍

• 程序员面试笔记
• 慕课网：数据算法与结构
• 其他…

树结构的一些基本定义

---

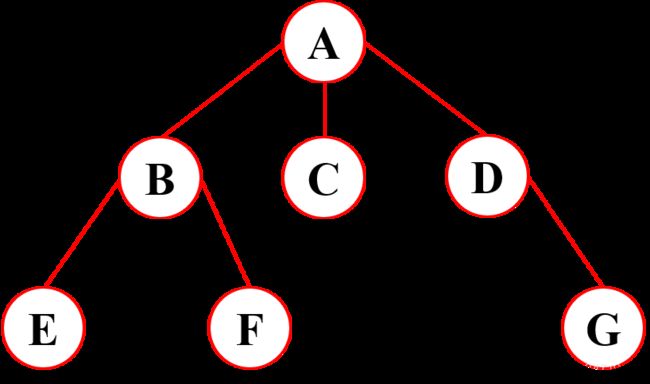
示意图

• 结点的度：结点拥有的子树的数目。eg：结点 A 的度为3
• 树的度：树种各结点度的最大值。eg：树的度为3
• 叶子结点：度为 0 的结点。g：E、F、C、G 为叶子结点
• 孩子结点：一个结点的子树的根节点。eg：B、C、D 为 A 的子结点
• 双亲结点：B 为 A 的子结点，那么 A 为 B 的双亲结点
• 兄弟结点：一个双亲结点结点的孩子互为兄弟结点。eg：B、C、D 为兄弟结点
• 结点的层次：根节点为第一层，子结点为第二层，依次向下递推…eg：E、F、G 的层次均为 3
• 树的深度：树种结点的最大深度。eg：该树的深度为 3
• 森林：m 棵互不相交的树称为森林

树结构的性质

---

1. 非空树的结点总数等于树种所有结点的度之和加 1
2. 度为 K 的非空树的第 i 层最多有 k^i-1 个结点(i >= 1)
3. 深度为 h 的 k 叉树最多有(k^h - 1)/(k - 1)个结点
4. 具有 n 个结点的 k 叉树的最小深度为 log_k(n(k-1)+1))

二叉树(Binary-Tree)

---

二叉树的定义

二叉树是一种特殊的树：它或者为空，或者由一个根节点加上根节点的左子树和右子树组成，这里要求左子树和右子树互不相交，且同为二叉树，很显然，这个定义是递归形式的。

满二叉树与完全二叉树

满二叉树： 如果一棵二叉树的任意一个结点或者是叶子结点，或者有两棵子树，同时叶子结点都集中在二叉树的最下面一层上，这样的二叉树称为满二叉树

完全二叉树： 若二叉树中最多只有最下面两层结点的度小于 2 ，并且最下面一层的结点（叶子结点）都依次排列在该层最左边的位置上，具有这样结构特点的树结构称为完全二叉树。

二叉树的性质

1. 在二叉树中第 i 层上至多有 2^i-1 个结点(i >=1)
2. 深度为 k 的二叉树至多有 2^k-1 个结点(k >=1)
3. 对于任何一棵二叉树，如果其叶子结点数为 n₀ ，度为 2 的结点数为 n₂ ，那么 n₀ = n₂ + 1
4. 具有 n 个结点的完全二叉树的深度为 log₂n + 1

结点定义

typedef struct BiTNode{
	ElemType data;
	struct BiTNode * lchild, * rchild;
} BiTNode, *BiTree;

二叉树的创建

/*创建一棵二叉树*/
void CreatBiTree(BiTree *T) {
    char c;
    scanf("%c", &c);
    if(c == ' ') *T = NULL;
    else {
        *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
        (*T)->data = c;    /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
    }
}

二叉树的遍历

基于深度遍历二叉树

分为先序(DLR)、中序(LDR)、后序遍历(LRD)

#include "stdio.h"
#include "malloc.h"

typedef struct BiTNode {
    char data;   /*结点的数据域*/
    struct BiTNode *lchild, *rchild;   /*指向左孩子和右孩子*/
} BiTNode, *BiTree;

/*创建一棵二叉树*/
void CreatBiTree(BiTree *T) {
    char c;
    scanf("%c", &c);
    if(c == ' ') *T = NULL;
    else {
        *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
        (*T)->data = c;    /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
    }
}

/*前序遍历二叉树*/
void PreOrderTraverse(BiTree T ) {
    if(T) {  /*递归结束条件，T为空*/
        printf("%3c", T->data); /*访问根结点,将根结点内容输出*/
        PreOrderTraverse(T->lchild);  /*先序遍历T的左子树*/
        PreOrderTraverse(T->rchild);  /*先序遍历T的右子数*/
    }
}

/*中序遍历二叉树*/
void InOrderTraverse(BiTree T) {
    if(T) {  /*如果二叉树为空，递归遍历结束*/
        InOrderTraverse(T->lchild);  /*中序遍历T的左子树*/
        printf("%3c", T->data);      /*访问根结点*/
        InOrderTraverse(T->rchild);  /*中序遍历T的右子数*/
    }
}

/*后序遍历二叉树*/
void PosOrderTraverse(BiTree T) {
    if(T) {  /*如果二叉树为空，递归遍历结束*/
        PosOrderTraverse(T->lchild);  /*后序遍历T的左子树*/
        PosOrderTraverse(T->rchild);  /*后序遍历T的右子数*/
        printf("%3c", T->data);       /*访问根结点*/
    }
}


int main() {
    BiTree T = NULL;  /*最开始T指向空*/
    printf("Input some characters to create a binary tree\n");
    CreatBiTree(&T);  /*创建二叉树*/
    printf("The squence of preorder traversaling binary tree\n");
    PreOrderTraverse(T); /*先序遍历二叉树*/
    printf("\nThe squence of inorder traversaling binary tree\n");
    InOrderTraverse(T);  /*中序遍历二叉树*/
    printf("\nThe squence of posorder traversaling binary tree\n");
    PosOrderTraverse(T); /*后序遍历二叉树*/
    getchar();
    getchar();
}

基于层次遍历二叉树

方法一

#include "stdio.h"

typedef struct BiTNode {
   char data;   /*结点的数据域*/
   struct BiTNode *lchild, *rchild;   /*指向左孩子和右孩子*/
} BiTNode, *BiTree;

/*创建一棵二叉树*/
void CreatBiTree(BiTree *T) {
   char c;
   scanf("%c", &c);
   if(c == ' ') *T = NULL;
   else {
      *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
      (*T)->data = c;    /*向根结点中输入数据*/
      CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
      CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
   }
}

/*遍历二叉树*/
void PreOrderTraverse(BiTree T ) {
   if(T) {  /*递归结束条件，T为空*/
      printf("%3c", T->data); /*访问根结点,将根结点内容输出*/
      PreOrderTraverse(T->lchild);  /*先序遍历T的左子树*/
      PreOrderTraverse(T->rchild);  /*先序遍历T的右子数*/
   }
}

void visit(BiTree p) {
   printf("%3c", p->data);
}

void layerOrderTraverse(BiTree T) {
   BiTree queue[20], p;
   int front, rear;
   if(T != NULL) {
      queue[0] = T;       /*将根结点的指针（地址）入队列*/
      front = -1;
      rear = 0;
      while(front < rear) {   /*当队列不为空时进入循环*/
         p = queue[++front]; /*取出队头元素*/
         visit(p);       /*访问p指向的结点元素*/
         if(p->lchild != NULL) /*将p结点的左孩子结点指针入队列*/
            queue[++rear] = p->lchild;
         if(p->rchild != NULL) /*将p结点的右孩子结点指针入队列*/
            queue[++rear] = p->rchild;
      }
   }
}

main() {
   BiTree T = NULL;  /*最开始T指向空*/
   printf("Input some characters to create a binary tree\n");
   CreatBiTree(&T);  /*创建二叉树*/

   printf("\nThe squence of layerorder traversaling binary tree\n");
   layerOrderTraverse(T);
   getchar();
   getchar();
}

方法二

void layerOrderTraverse(BiTree T){
	BiTree p;
	queue<BiTree> q;
	if(T != NULL){
		q.push(T);
		while(!q.empty()){
			p = q.front();
			q.pop();
			visit(p);  // 自定义访问操作
			if(p->lchild != NULL)
				q.push(p->lchild);
			if(p->rchild != NULL)
				q.push(p->rchild);
		}
	}
}

二叉树的深度

方法一

#include "stdio.h"
#include "malloc.h"

typedef struct BiTNode{
    char data;   /*结点的数据域*/
    struct BiTNode *lchild , *rchild;  /*指向左孩子和右孩子*/
} BiTNode , *BiTree;

/*创建一棵二叉树*/
void CreatBiTree(BiTree *T)
{
    char c;
    scanf("%c",&c);
    if(c == ' ') *T = NULL;
    else{
       *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
        (*T)->data = c;    /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
    }
}

/*计算二叉树的深度*/
void getDepth(BiTree T,int n,int *level)
{
   if(T!=NULL)
   {
        if(n> *level)
        {
            *level = n;
        }
        getDepth(T->lchild,n+1,level);
        getDepth(T->rchild,n+1,level);
   }
}

int getBitreeDepth(BiTree T)
{
    int level = 0;
    int n = 1;
    getDepth(T,n,&level);
    return level ;
}

main()
{
    BiTree T = NULL;    /*最开始T指向空*/
    printf("Input some characters to create a binary tree \n");
    CreatBiTree(&T);    /*创建二叉树*/
    printf("\nThe depth of the binary tree is %d\n",getBitreeDepth(T));
    getchar() ;
	getchar() ;
}

方法二

int getBitreeDepth(BiTree T){
	int leftHeight, rightHeight, maxHeight;
	if(T != NULL){
		leftHeight = getBitreeDepth(T->lchild);  // 计算左子树的深度
		rightHeight = getBitreeDepth(T->rchild);  // 计算右子树的深度
		maxHeight = leftHeight > rightHeight ? leftHeight : rightHeight;  // 比较左右子树的深度
		return maxHeight + 1;  // 返回二叉树的深度
	else{
		return 0;
	}
}

二叉树叶子结点个数

#include "string.h" 
#include "stdio.h" 
#include "malloc.h"

typedef struct BiTNode{
    char data;   /*结点的数据域*/
    struct BiTNode *lchild , *rchild;  /*指向左孩子和右孩子*/
} BiTNode , *BiTree;

void CreatBiTree(BiTree *T){
    char c;
    scanf("%c",&c);
    if(c == ' ') *T = NULL;
    else{
       *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
        (*T)->data = c;    /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
    }
}

void getLeavesConut (BiTree T,int *count){
    if(T!=NULL && T->lchild==NULL && T->rchild==NULL){   /*访问到叶结点*/
        *count = *count + 1;
    }
    if(T){
        getLeavesConut (T->lchild,count);  /*先序遍历T的左子树*/
        getLeavesConut (T->rchild,count);  /*先序遍历T的右子数*/
    }
}

int getBiTreeLeavesCount(BiTree T) {
	int count = 0;				/*在主调函数中定义变量count，初始值为0*/
	getLeavesConut(T, &count);	/*调用递归函数getLeavesConut计算叶子结点个数*/
	return count;				/*返回叶子结点个数*/
}

main()
{
   BiTree T = NULL;				/*初始化T */
   int count = 0;
   printf("Input some characters to create a binary tree \n");
   CreatBiTree(&T);				/*创建一棵二叉树*/
   getLeavesConut (T,&count);	/*计算二叉树中叶子结点的个数 */
   printf("The number of leaves of BTree are %d\n",count);
   getchar();
   getchar();
}

二叉排序树(Binary-Sort-Tree)

---

什么是二叉排序树

二又排序树或者为一棵空树，或者是具有下列性质的二又树：

1. 若它的左子树不为空，则左子树上的所有结点的值均小于根结点的值
2. 若它的右子树不为空，则右子树上的所有结点的值均大于根节点的值
3. 二叉排序树的左右子树也都是二叉排序树

二叉排序树的查找

BiTree SearchBST(BiTree T, dataTYpe){
	if(T == NULL)
		return NULL;
	if(T->data == key)
		return T;
	if(key < T->data)
		return SearchBST(T-> lchild, key);
	else
		return SearchBST(T-> rchild, key);
}

最低公共祖先

分析

从整棵二又排序树的根结点出发，
当访间的当前结点同时大于给定的两个结点时、沿左指前进；
当访间的当前结点同时小于給定的两个结点时，沿右指针前进；
当第一次访问到介于给定的两个结点值之间的那个结点时即是它们的最低公共祖先结点

然鹅，这个算法并不完善，因为这个算法适用的前提是给定的两个结点分别位于二叉排序树中某个结点的左右子树上

假设给定的两个结点分别为a和b，并且 a 是 b 的祖先，那么结点 a 和 b 的最低公共祖先就是 a 的父结点，因为 a 的父结点一定也是 b 的祖先，同时该结点也必然是 a 和 b 的最低公共祖先。

另外，如果给定的 a 或 b 其中一个为根结点的值，那么这种情况是不存在公共最低祖先的，因为根结点没有祖先，所以也应把这种情况考虑进去。

#include "stdio.h"
#include "malloc.h"
#include "string.h"

typedef struct BiTNode{
    int data;   /*结点的数据域*/
    struct BiTNode *lchild;
    struct BiTNode *rchild;  /*指向左孩子和右孩子*/
} BiTNode , *BiTree;

int findLowestCommonAncestor(BiTree T,int value1, int value2) {
	BiTree curNode = T;  /*curNode为当前访问结点，初始化为T*/
	if(T->data == value1 || T->data == value2) {
		return -1;    /*value1和value2有一个为根结点，因此没有公共祖先，返回-1*/
	}
	while(curNode != NULL){
		if (curNode->data > value1 &&
			curNode->data > value2 && curNode->lchild->data != value1 &&
			curNode->lchild->data != value2) {
/*当前结点的值同时大于value1和value2，且不是value1和value2的父结点*/
				curNode = curNode->lchild;  
		} else if (curNode->data < value1 &&
			curNode->data < value2 && curNode->rchild->data != value1 &&
			curNode->rchild->data != value2) {
/*当前结点的值同时小于value1和value2，且不是value1和value2的父结点*/
				curNode = curNode->rchild;
		} else {
			return curNode->data;	/*找到最低公共祖先*/
		}
	}
}

void CreatBiTree(BiTree *T){
    int d;
    scanf("%d",&d);
    if(d == 0) *T = NULL;
    else{
       *T = (BiTNode * )malloc(sizeof(BiTNode));  /*创建根结点*/
        (*T)->data = d;    /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));  /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));  /*递归地创建右子树*/
    }
}

main()
{
	BiTree T;
	int value1,value2;
	int ancestorValue;
	printf("Please create a binary sort tree\n");
	CreatBiTree(&T);
	printf("Input two values for searching lowest common ancestor\n");
	scanf("%d,%d",&value1,&value2);
	ancestorValue = findLowestCommonAncestor(T,value1,value2);
	if (ancestorValue != -1) {
		printf("The  lowest common ancestor is %d\n", ancestorValue);
	} else {
		printf("There is no ancestor\n");
	}
	getchar();
}

二叉排序树 VS 二叉堆(Binary-Heap)

---

两者的相同点与不同点

相同点

二叉堆也是一种树结构

不同点

1. 任何一个结点都不大于父亲节点（亦即左右结点均不大于父节点）
2. 必须是一棵完全二叉树（结点必须集中在最左侧），亦即最大堆
3. 用数组存储二叉堆，原因在于满二叉树的结点索引存在倍数关系

关系描述为：左结点是父节点的 2 倍，右结点为父节点的 2 倍 加 1（根结点的序列为 1）

二叉堆主要表现为最大堆(Max-Heap)，主要涉及以下内容

最大堆的一些基本操作(Max-Heap)

• 创建
• 删除
• 元素个数
• 插入
• 堆顶元素
• 最大元素

#include 
#include 

using namespace std;

template<typename Item>
class MaxHeap{

private:
    Item *data;
    int count;
    int capacity;

    void shiftUp(int k){
        while( k > 1 && data[k/2] < data[k] ){
            swap( data[k/2], data[k] );
            k /= 2;
        }
    }

    void shiftDown(int k){
        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[j+1] > data[j] ) j ++;
            if( data[k] >= data[j] ) break;
            swap( data[k] , data[j] );
            k = j;
        }
    }

public:

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    MaxHeap(int capacity){
        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    MaxHeap(Item arr[], int n){
        data = new Item[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;

        for( int i = count/2 ; i >= 1 ; i -- )
            shiftDown(i);
    }

    ~MaxHeap(){
        delete[] data;
    }

    // 返回堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 像最大堆中插入一个新的元素 item
    void insert(Item item){
        assert( count + 1 <= capacity );
        data[count+1] = item;
        shiftUp(count+1);
        count ++;
    }

    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    Item extractMax(){
        assert( count > 0 );
        Item ret = data[1];
        swap( data[1] , data[count] );
        count --;
        shiftDown(1);
        return ret;
    }

    // 获取最大堆中的堆顶元素
    Item getMax(){
        assert( count > 0 );
        return data[1];
    }
};

最大索引堆(Max-Heap-Index)

#include 
#include 

using namespace std;

// 最大索引堆
template<typename Item>
class IndexMaxHeap{

private:
    Item *data;     // 最大索引堆中的数据
    int *indexes;   // 最大索引堆中的索引, indexes[x] = i 表示索引i在x的位置
    int *reverse;   // 最大索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置

    int count;
    int capacity;

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftUp( int k ){

        while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
            swap( indexes[k/2] , indexes[k] );
            reverse[indexes[k/2]] = k/2;
            reverse[indexes[k]] = k;
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftDown( int k ){

        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
                j += 1;

            if( data[indexes[k]] >= data[indexes[j]] )
                break;

            swap( indexes[k] , indexes[j] );
            reverse[indexes[k]] = k;
            reverse[indexes[j]] = j;
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
    IndexMaxHeap(int capacity){

        data = new Item[capacity+1];
        indexes = new int[capacity+1];
        reverse = new int[capacity+1];
        for( int i = 0 ; i <= capacity ; i ++ )
            reverse[i] = 0;

        count = 0;
        this->capacity = capacity;
    }

    ~IndexMaxHeap(){
        delete[] data;
        delete[] indexes;
        delete[] reverse;
    }

    // 返回索引堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    void insert(int i, Item item){
        assert( count + 1 <= capacity );
        assert( i + 1 >= 1 && i + 1 <= capacity );

        // 再插入一个新元素前,还需要保证索引i所在的位置是没有元素的。
        assert( !contain(i) );

        i += 1;
        data[i] = item;
        indexes[count+1] = i;
        reverse[i] = count+1;
        count++;

        shiftUp(count);
    }

    // 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
    Item extractMax(){
        assert( count > 0 );

        Item ret = data[indexes[1]];
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 从最大索引堆中取出堆顶元素的索引
    int extractMaxIndex(){
        assert( count > 0 );

        int ret = indexes[1] - 1;
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 获取最大索引堆中的堆顶元素
    Item getMax(){
        assert( count > 0 );
        return data[indexes[1]];
    }

    // 获取最大索引堆中的堆顶元素的索引
    int getMaxIndex(){
        assert( count > 0 );
        return indexes[1]-1;
    }

    // 看索引i所在的位置是否存在元素
    bool contain( int i ){
        assert( i + 1 >= 1 && i + 1 <= capacity );
        return reverse[i+1] != 0;
    }

    // 获取最大索引堆中索引为i的元素
    Item getItem( int i ){
        assert( contain(i) );
        return data[i+1];
    }

    // 将最大索引堆中索引为i的元素修改为newItem
    void change( int i , Item newItem ){

        assert( contain(i) );
        i += 1;
        data[i] = newItem;

        // 找到indexes[j] = i, j表示data[i]在堆中的位置
        // 之后shiftUp(j), 再shiftDown(j)
//        for( int j = 1 ; j <= count ; j ++ )
//            if( indexes[j] == i ){
//                shiftUp(j);
//                shiftDown(j);
//                return;
//            }

        // 有了 reverse 之后,
        // 我们可以非常简单的通过reverse直接定位索引i在indexes中的位置
        shiftUp( reverse[i] );
        shiftDown( reverse[i] );
    }
};

堆排序

#include 
#include 

// 优化的shiftDown过程, 使用赋值的方式取代不断的swap,
// 该优化思想和我们之前对插入排序进行优化的思路是一致的
template<typename T>
void __shiftDown(T arr[], int n, int k){

    T e = arr[k];
    while( 2*k+1 < n ){
        int j = 2*k+1;
        if( j+1 < n && arr[j+1] > arr[j] )
            j += 1;

        if( e >= arr[j] ) break;

        arr[k] = arr[j];
        k = j;
    }

    arr[k] = e;
}

// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort(T arr[], int n){

    // 注意，此时我们的堆是从0开始索引的
    // 从(最后一个元素的索引-1)/2开始
    // 最后一个元素的索引 = n-1
    for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
        __shiftDown2(arr, n, i);

    for( int i = n-1; i > 0 ; i-- ){
        swap( arr[0] , arr[i] );
        __shiftDown(arr, i, 0);
    }
}

二分搜索树(Binary-Search-Tree)

---

什么是二分搜索树

二分搜索树具有以下特点

• 依然是一棵二叉树
• 每个结点大与左孩子
• 每个结点大于右孩子
• 以左右孩子为根的子树仍然是二分搜索树
• 不存在相同的结点
• 不一定是完全二叉树
• 用 Node 结点来表示

二分搜索树的一些基本操作

• 创建
• 删除
• 结点个数
• 插入
• 判断是否存在一个元素
• 前序遍历
• 中序遍历
• 后序遍历
• 删除最大值
• 删除最小值
• 删除指定值

#include 
#include 
#include 

using namespace std;

// 二分搜索树
template <typename Key, typename Value>
class BST{

private:
    // 树中的节点为私有的结构体, 外界不需要了解二分搜索树节点的具体实现
    struct Node{
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key key, Value value){
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }

        Node(Node *node){
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
        }
    };

    Node *root; // 根节点
    int count;  // 树中的节点个数

public:
    // 构造函数, 默认构造一棵空二分搜索树
    BST(){
        root = NULL;
        count = 0;
    }

    // 析构函数, 释放二分搜索树的所有空间
    ~BST(){
        destroy( root );
    }

    // 返回二分搜索树的节点个数
    int size(){
        return count;
    }

    // 返回二分搜索树是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    void insert(Key key, Value value){
        root = insert(root, key, value);
    }

    // 查看二分搜索树中是否存在键key
    bool contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL
    Value* search(Key key){
        return search( root , key );
    }

    // 二分搜索树的前序遍历
    void preOrder(){
        preOrder(root);
    }

    // 二分搜索树的中序遍历
    void inOrder(){
        inOrder(root);
    }

    // 二分搜索树的后序遍历
    void postOrder(){
        postOrder(root);
    }

    // 二分搜索树的层序遍历
    void levelOrder(){

        queue<Node*> q;
        q.push(root);
        while( !q.empty() ){

            Node *node = q.front();
            q.pop();

            cout<<node->key<<endl;

            if( node->left )
                q.push( node->left );
            if( node->right )
                q.push( node->right );
        }
    }

    // 寻找二分搜索树的最小的键值
    Key minimum(){
        assert( count != 0 );
        Node* minNode = minimum( root );
        return minNode->key;
    }

    // 寻找二分搜索树的最大的键值
    Key maximum(){
        assert( count != 0 );
        Node* maxNode = maximum(root);
        return maxNode->key;
    }

    // 从二分搜索树中删除最小值所在节点
    void removeMin(){
        if( root )
            root = removeMin( root );
    }

    // 从二分搜索树中删除最大值所在节点
    void removeMax(){
        if( root )
            root = removeMax( root );
    }

    // 从二分搜索树中删除键值为key的节点
    void remove(Key key){
        root = remove(root, key);
    }

private:
    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    Node* insert(Node *node, Key key, Value value){

        if( node == NULL ){
            count ++;
            return new Node(key, value);
        }

        if( key == node->key )
            node->value = value;
        else if( key < node->key )
            node->left = insert( node->left , key, value);
        else    // key > node->key
            node->right = insert( node->right, key, value);

        return node;
    }

    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    bool contain(Node* node, Key key){

        if( node == NULL )
            return false;

        if( key == node->key )
            return true;
        else if( key < node->key )
            return contain( node->left , key );
        else // key > node->key
            return contain( node->right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    Value* search(Node* node, Key key){

        if( node == NULL )
            return NULL;

        if( key == node->key )
            return &(node->value);
        else if( key < node->key )
            return search( node->left , key );
        else // key > node->key
            return search( node->right, key );
    }

    // 对以node为根的二分搜索树进行前序遍历, 递归算法
    void preOrder(Node* node){

        if( node != NULL ){
            cout<<node->key<<endl;
            preOrder(node->left);
            preOrder(node->right);
        }
    }

    // 对以node为根的二分搜索树进行中序遍历, 递归算法
    void inOrder(Node* node){

        if( node != NULL ){
            inOrder(node->left);
            cout<<node->key<<endl;
            inOrder(node->right);
        }
    }

    // 对以node为根的二分搜索树进行后序遍历, 递归算法
    void postOrder(Node* node){

        if( node != NULL ){
            postOrder(node->left);
            postOrder(node->right);
            cout<<node->key<<endl;
        }
    }

    // 释放以node为根的二分搜索树的所有节点
    // 采用后续遍历的递归算法
    void destroy(Node* node){

        if( node != NULL ){
            destroy( node->left );
            destroy( node->right );

            delete node;
            count --;
        }
    }

    // 返回以node为根的二分搜索树的最小键值所在的节点, 递归算法
    Node* minimum(Node* node){
        if( node->left == NULL )
            return node;

        return minimum(node->left);
    }

    // 返回以node为根的二分搜索树的最大键值所在的节点, 递归算法
    Node* maximum(Node* node){
        if( node->right == NULL )
            return node;

        return maximum(node->right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node* removeMin(Node* node){

        if( node->left == NULL ){

            Node* rightNode = node->right;
            delete node;
            count --;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node* removeMax(Node* node){

        if( node->right == NULL ){

            Node* leftNode = node->left;
            delete node;
            count --;
            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }

    // 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node* remove(Node* node, Key key){

        if( node == NULL )
            return NULL;

        if( key < node->key ){
            node->left = remove( node->left , key );
            return node;
        }
        else if( key > node->key ){
            node->right = remove( node->right, key );
            return node;
        }
        else{   // key == node->key

            if( node->left == NULL ){
                Node *rightNode = node->right;
                delete node;
                count --;
                return rightNode;
            }

            if( node->right == NULL ){
                Node *leftNode = node->left;
                delete node;
                count--;
                return leftNode;
            }

            // node->left != NULL && node->right != NULL
            Node *successor = new Node(minimum(node->right));
            count ++;

            successor->right = removeMin(node->right);
            successor->left = node->left;

            delete node;
            count --;

            return successor;
        }
    }
};

四叉树(Quad-Tree)

---

什么是四叉树

参考博客：四叉树空间索引原理及其实现

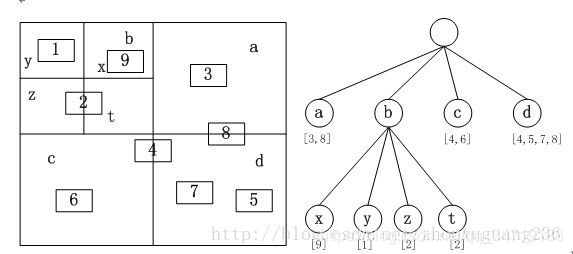
四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。它将已知范围的空间等分成四个相等的子空间，如此递归下去，直至树的层次达到一定深度或者满足某种要求后停止分割。

四叉树的结构比较简单，并且当空间数据对象分布比较均匀时，具有比较高的空间数据插入和查询效率，因此四叉树是GIS中常用的空间索引之一。

常规四叉树的结构如图所示，地理空间对象都存储在叶子节点上，中间节点以及根节点不存储地理空间对象。

四叉树的一些应用

参考博客：一个四叉树的简单实现

参考博客：四叉树Quadtrees在游戏领域应用

八叉树(Octree)

---

参考博客：八叉树（Octree）

参考博客：八叉树

参考博客：八叉树及K-D树的应用和实现

参考博客：图像量化法——八叉树算法

kd 树(Kd-Tree)

---

参考博客：Kd-Tree算法原理简析

参考博客：KDTree

参考博客：KD tree

参考博客：详解 KDTree

红黑树(Red-Black-Tree)

---

参考博客：红黑树(一)之 原理和算法详细介绍

参考博客：红黑树(二)之 C语言的实现

参考博客：红黑树(三)之 Linux内核中红黑树的经典实现

参考博客：红黑树(四)之 C++的实现

参考博客：红黑树(六)之 参考资料

哈夫曼树(Huffman-Tree)

---

定义

具有最小带权路径长度的二叉树称为哈夫曼树。

参考博客：哈夫曼树

参考博客：哈夫曼树与哈夫曼编码

参考博客：哈夫曼树

参考博客：哈夫曼树