初级排序算法(algs4)
1.规则
排序类算法模板API
| public class Example |
|
|
| public static void sort(Comparable[] a) (**)排序 private static boolean less(Comparable v,Comparable w) 比较 private static void exch(Comparable[] a,int i,int j) 交换 private static void show(Comparable[] a) 打印数组 private static boolean isSorted(Comparable[] a) 判断数组元素是否有序 public static void main(String[] args) 读取,排序,输出 |
排序算法模板适用于任何实现了 Comparable接口的数据类型。
很多数据类型都实现了 Comparable 接口。例如,Java 中封装数字的类型 Integer 和 Double,以及 String 和其他许多高级数据类型(如 File 和 URL)都实现了Comparable接口。
在创建自己的数据类型时,我们只要实现 Comparable 接口就能够保证用例代码可以将其排序。要做到这一点,只需要实现一个 compareTo() 方法来定义目标类型对象的自然次序。
package _2_Sorting;
import java.util.Scanner;
/*排序算法类的模板
*/
public class Example
{
public static void sort(Comparable[] a)
{
/*各种排序*/
}
private static boolean less(Comparable v,Comparable w)
{
return v.compareTo(w)<0;
}
private static void exch(Comparable[] a,int i,int j)
{
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a)
{
for(int i=0;i
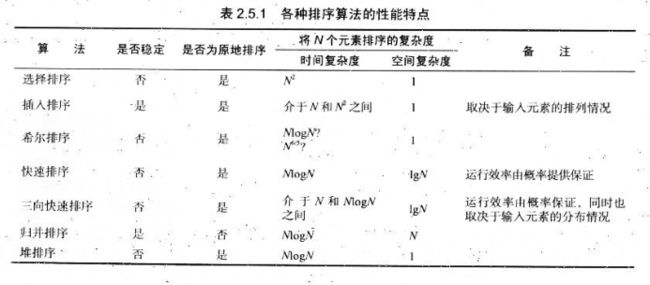
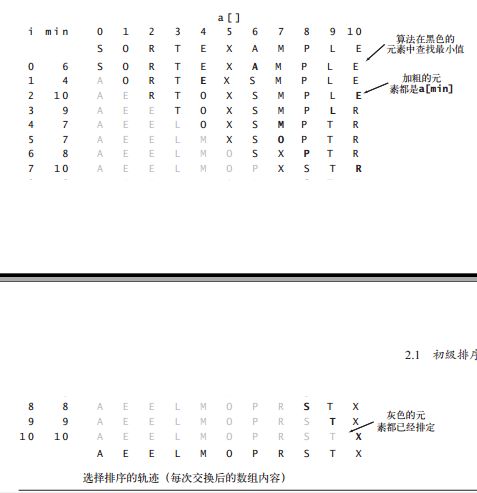
2.选择排序
首先,找到数组中最小的那个元素,
其次,将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。
再次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。
如此往复,直到将整个数组排序。
这种方法叫做选择排序,
因为它在不断地选择剩余元素之中的最小者。
/**算法2.1选择排序(Selection sort)
* 该算法将第 i 小的元素放到 a[i] 之中。数组的第 i 个位置的左边是 i 个最小的元素且它们不会再被访问。
* 特点:
* 1. 运行时间和输入无关
* 2. 数据移动是最少的
* 对于长度为 N 的数组,选择排序需要大约 N^2/2 次比较和 N 次交换。
* */
public static void sort(Comparable[] a)
{
for(int i=0;i/**
* 算法2.1选择排序(Selection sort)
* 改进版
* 用k来记录剩余元素中最小数的索引
* 只有找到剩下元素中最小的才进行交换
* 减少了交换次数
*/
public static void sort(Comparable[] a) {
int k = 0;
for (int i = 0; i < a.length; i++) {
k=i;
for (int j = k + 1; j < a.length; j++) {
if (less(a[j], a[k])) {
k=j; //确保k记录的是最小数的索引
}
}
if (k!=i) {
exch(a,i,k);
}
}
}另:
/**
* 冒泡排序
*/
public static void sort(Comparable[] a) {
for (int i = a.length - 1; i >= 1; i--) {
for (int j = 0; j <= i - 1; j++) {
if (less(a[j + 1], a[j])) {
exch(a[j + 1], a[j]);
}
}
}
}3.插入排序
选择排序一样,当前索引左边的所有元素都是有序的,但它们的最终位置还不确定,为了给更小的元素腾出空间,它们可能会被移动。但是当索引到达数组的右端时,数组排序就完成了
/**算法2.2插入排序(Insertion sort)
* 对于 0 到 N-1 之间的每一个 i,将 a[i] 与 a[0] 到 a[i-1] 中比它小的所有元素依次有序地交换。
* 在索引 i 由左向右变化的过程中,它左侧的元素总是有序的,所以当 i 到达数组的右端时排序就完成了。
* 插入排序需要的交换操作和数组中倒置的数量相同,
* 需要的比较次数大于等于倒置的数量,小于等于倒置的数量加上数组的大小再减一。
* 要大幅提高插入排序的速度并不难,
* 只需要在内循环中将较大的元素都向右移动而不总是交换两个元素(这样访问数组的次数就能减半)。
* */
public static void sort(Comparable[] a)
{
for(int i=1;i0&&less(a[j],a[j-1]);j--) /*将 a[i] 插入到 a[i-1]、a[i-2]、a[i-3]...之中*/
exch(a,j,j-1);
} 4.比较
插入排序不会访问索引右侧的元素,而选择排序不会访问索引左侧的元素。
另外,在这种可视化的轨迹图中可以看到,因为插入排序不会移动比被插入的元素更小的元素,它所需的比较次数平均只有选择排序的一半。
对于随机排序的无重复主键的数组,插入排序和选择排序的运行时间是平方级别的,两者之比应该是一个较小的常数。
5.希尔排序
希尔排序为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序,并最终用插入排序将局部有序的数组排序
希尔排序的思想是使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组。
换句话说,一个 h 有序数组就是 h 个互相独立的有序数组编织在一起组成的一个数组。
在进行排序时,如果 h 很大,我们就能将元素移动到很远的地方,为实现更小的 h 有序创造方便。用这种方式,对于任意以 1 结尾的 h 序列,我们都能够将数组排序。这就是希尔排序。
算法 2.3 的实现使用了序列 1/2(3^k-1),从 N/3 开始递减至 1。我们把这个序列称为递增序列。算法 2.3 实时计算了它的递增序列,另一种方式是将递增序列存储在一个数组中。
/**算法2.3希尔排序(Shellsort)
* 如果我们在插入排序中加入一个外循环来将 h 按照递增序列递减,我们就能得到这个简洁的希尔排序。
* 增幅 h 的初始值是数组长度乘以一个常数因子,最小为 1。
* 实际上,算法 2.3 是我们唯一无法准确描述其对于乱序的数组的性能特征的排序方法。
* */
private static void sort(Comparable[] a)
{
int N=a.length;
int h=1;
while(h=1)
{ /*将数组变为h有序*/
for(int i=h;i=h&&less(a[j],a[j-h]);j=j-h) /*j>=h!!!*/
exch(a,j,j-h);
h=h/3;
}
} 
希尔排序比插入排序和选择排序要快得多,并且数组越大,优势越大。
由插入排序到希尔排序,一个小小的改变就突破了平方级别的运行时间的屏障。
如果需要解决一个排序问题而又没有系统排序函数可用(例如直接接触硬件或是运行于嵌入式系统中的代码),可以先用希尔排序,然后再考虑是否值得将它替换为更加复杂的排序算法。
6.附录
package _2_Sorting;
import java.util.Scanner;
/*排序算法类的模板
* 升序
*/
public class Example
{
/**算法2.1 选择排序(Selection sort)
* 该算法将第 i 小的元素放到 a[i] 之中。数组的第 i 个位置的左边是 i 个最小的元素且它们不会再被访问。
* 特点:
* 1. 运行时间和输入无关
* 2. 数据移动是最少的
* 对于长度为 N 的数组,选择排序需要大约 N^2/2 次比较和 N 次交换。
* */
// public static void sort(Comparable[] a)
// {
// for(int i=0;i0&&less(a[j],a[j-1]);j--)
// exch(a,j,j-1);
// }
/**算法2.3希尔排序(Shellsort)
* 如果我们在插入排序中加入一个外循环来将 h 按照递增序列递减,我们就能得到这个简洁的希尔排序。
* 增幅 h 的初始值是数组长度乘以一个常数因子,最小为 1。
* 实际上,算法 2.3 是我们唯一无法准确描述其对于乱序的数组的性能特征的排序方法。
* */
private static void sort(Comparable[] a)
{
int N=a.length;
int h=1;
while(h=1)
{ /*将数组变为h有序*/
for(int i=h;i=h&&less(a[j],a[j-h]);j=j-h) /*j>=h!!!*/
exch(a,j,j-h);
h=h/3;
}
}
private static boolean less(Comparable v,Comparable w)
{
return v.compareTo(w)<0;
}
private static void exch(Comparable[] a,int i,int j)
{
Comparable t=a[i];
a[i]=a[j];
a[j]=t;
}
private static void show(Comparable[] a)
{
for(int i=0;i