Decision tree(决策树)
(注:本文并非原创,但修改了原文中几处代码错误以及部分概念描述的模糊之处,新加了一些算式证明等)
决策树是广泛用于分类和回归任务的模型。本质上,它从一层层if/else问题中进行学习,并得出结论
import mglearn
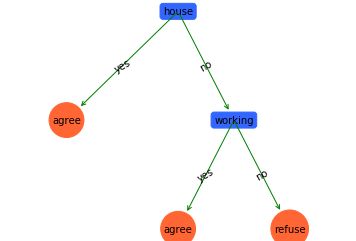
mglearn.plots.plot_animal_tree()
上图就是一颗决策树,树的每个结点代表一个问题或包含答案的终结点(也叫叶结点)
下面较为详细的解释下这个算法:首先,决策树是一种基本的分类与回归方法
在分类中,定义为:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型:内部结点和叶结点,内部结点表示一个特征或属性,叶结点表示一个类。
分类的时候,从根结点开始,对实例的某一个特征进行测试,根据测试结果,将实例分配到其子结点;此时,每一个子结点对应着该特征的一个取值。如此递归向下移动,直至达到叶结点,最后将实例分配到叶结点的类中。
决策树的学习
决策树学习算法包含特征选择、决策树的生成与剪枝过程。决策树的学习算法通常是递归地选择最优特征,并用最优特征对数据集进行分割。开始时,构建根结点,选择最优特征,该特征有几种值就分割为几个子集,每个子集分别递归调用此方法,返回结点,返回的结点就是上一层的子结点。直到所有特征都已经用完,或者数据集只有一维特征为止。
特征选择
特征选择问题希望选取对训练数据具有良好分类能力的特征,这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。为了更好的选择特征,使用了一些熵的概念(在另外的文章中已经详细推导过),这里用代码实现一下之前的结论
import numpy as np
def calcuInfoEnt(dataSet, i=-1):
'''
计算信息熵
dataSet:数据集
return:数据集的信息熵
'''
numElements = len(dataSet)
labelCounts = {}
infoEnt = 0.0
for elementVec in dataSet: #遍历数据集,统计元素向量中具有相同标签的频率
currLabel = elementVec[i]
if currLabel not in labelCounts.keys():
labelCounts[currLabel] = 0
labelCounts[currLabel] += 1
for key in labelCounts:
prob = float(labelCounts[key]) / numElements
infoEnt -= prob * np.log2(prob)
return infoEnt
def splitDataSet(dataSet, axis, featVal):
'''
按照给定特征值划分数据集
dataSet:待划分数据集
axis:划分数据集特征的维度
featVal:特征的值
return:划分的子数据集
'''
subDataSet = []
for elementVec in dataSet:
if elementVec[axis] == featVal:
reduceElemVec = elementVec[:axis] #提取特征前的vec
reduceElemVec.extend(elementVec[axis+1:]) #提取特征后的vec
subDataSet.append(reduceElemVec)
return subDataSet
def calcuConditionEnt(dataSet, i, featList, featSet):
'''
计算在指定特征i的条件下,Y的条件熵
dataSet:数据集
i:维度i
featList:数据集特征值列表
featSet:数据集特征值集合
'''
conditionEnt = 0.0
for featVal in featSet:
subDataSet = splitDataSet(dataSet, i, featVal)
prob = float(len(subDataSet))/len(dataSet) #指定特征的概率
conditionEnt += prob * calcuInfoEnt(subDataSet) #条件熵的定义计算
return conditionEnt
最一开始我们使用信息增益(Information gain)来构建决策树,被称为ID3,这种算法本身缺陷很大
Information gain(信息增益)
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。特征A对训练数据集D的信息增益 ,定义为集合D的经验熵 与特征A给定条件下D的经验条件熵H(D|A)之差,即
不难发现,信息增益大的特征具有更强的分类能力。那么,根据信息增益准则的特征选择方法就是:对训练数据集计算其每个特征的信息增益,选择信息增益最大的特征。
假设样本有k个类别, 表示类别k的样本个数, 表示样本总数,那么每个类别的概率就是
那么
特征A对数据集D的经验条件熵H(D|A):
根据特征A将D划分为n个子集 , 为 的样本个数, 之和为 ,记 中属于 的样本集合为 ,即交集, 为 的样本个数
def calcuInfoGain(dataSet, baseEnt, i):
'''
计算信息增益
dataSet:数据集
baseEnt:数据集的信息熵
i:特征维度
return:特征i对数据集的信息增益g(D|A)
'''
featList = [example[i] for example in dataSet] #第i维特征列表
featSet = set(featList) #转换为特征集合
conditionEnt = calcuConditionEnt(dataSet, i, featList, featSet)
infoGain = baseEnt - conditionEnt
return infoGain
后面改进为使用信息增益比(Information gain ratio)生成决策树,它对ID3算法进行了以下改进:
1)使用信息增益比选择特征,克服了用信息增益选择特征时偏向选择取值多的特征的不足
2)在树构造的过程中进行剪枝
3)能够完成对连续属性的离散化处理
4)能够对不完整数据进行处理
针对上面四点下面的介绍对后两点并未进行优化
Information gain ratio (信息增益比)
特征A对训练数据集D的信息增益比
公式为:
特别地,其中 为对于数据集D,将当前特征A作为随机变量(取值为特征A的各个特征值),求得的经验熵
惩罚参数(penalty parameter):数据集D以特征A作为随机变量的熵的倒数,即:将特征A取值相同的样本划分到同一个子集中
def calcuInfoGainRatio(dataSet, baseEnt, i):
'''
计算信息增益比
dataSet:数据集
baseEnt:数据集的信息熵
i:特征维度
return:特征i对数据集的信息增益比gR(D,A)
'''
return calcuInfoGain(dataSet, baseEnt, i) / calcuInfoEnt(dataSet, i)
决策树的生成
ID3
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(max_depth=3, random_state=0)
tree.fit(X_train, y_train)
export_graphviz(tree, out_file="tree.dot", class_names=["malignant", "benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
上面了生成了一棵树,对照着说一下算法
输入:训练数据集D, 特征A,阈值
输出:决策树T
(1)若D中所有实例属于同一类 ,则T单结点树,并将类 作为该结点的类标记,返回T;
(2)若A=,则T为单结点树,并将D中实例数最大的类 作为该结点的类标记,返回T;
(3)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征 ;
(4)如果 的信息增益小于阈值 ,则置T为单结点树,并将D中实例树最大的类 作为该结点的类标记,返回T;
(5)否则,对 的每一可能值 ,依 将D分割为若干非空子集 ,将 中实例数最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T;
(6)对第i个子结点,以 为训练集,以 为特征集,递归地调用(1)~(5),得到子树 ,返回 。
import operator
def chooseBestFeatSplitID3(dataSet):
'''
选择最好的数据集划分方式
dataSet:数据集
return:划分结果
'''
numFeatures = len(dataSet[0]) - 1
baseEnt = calcuInfoEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
infoGain = calcuInfoGain(dataSet, baseEnt, i) #计算信息增益
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature #返回最优特征维度
def majorityClassify(classList):
'''
采用多数表决的方法决定结点的分类
classList:所有的类标签列表
return:出现次数最多的类
'''
classCount = {}
for cla in classList:
if cla not in classCount.keys():
classCount[cla] = 0
classCount[cla] += 1
sortClassCount = sorted(classCount.items(), key=operator.itemgetter(1),
reverse=True)
return sortClassCount[0][0]
def crtDecisionTree(dataSet, featLabels):
'''
创建决策树
dataSet:训练数据集
featLabels:所有特征标签
return:返回决策树字典
'''
classList = [element[-1] for element in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0] #所有的类标签都相同
if len(dataSet[0]) == 1:
return majorityClassify(classList) #用完所有特征
bestFeat = chooseBestFeatSplitID3(dataSet)
bestFeatLabel = featLabels[bestFeat]
deTree = {bestFeatLabel:{}}
subFeatLabels = featLabels[:] #复制所有类标签,保证每次递归调用时不改变原来的
del(subFeatLabels[bestFeat])
featValues = [element[bestFeat] for element in dataSet]
featValSet = set(featValues)
#####
for value in featValSet:
#subFeatLabels = featLabels[:]
deTree[bestFeatLabel][value] = \
crtDecisionTree(splitDataSet(dataSet, bestFeat, value),subFeatLabels)
return deTree
# 导入数据
def createDataSet():
dataSet = [['youth', 'no', 'no', 1, 'refuse'],
['youth', 'no', 'no', '2', 'refuse'],
['youth', 'yes', 'no', '2', 'agree'],
['youth', 'yes', 'yes', 1, 'agree'],
['youth', 'no', 'no', 1, 'refuse'],
['mid', 'no', 'no', 1, 'refuse'],
['mid', 'no', 'no', '2', 'refuse'],
['mid', 'yes', 'yes', '2', 'agree'],
['mid', 'no', 'yes', '3', 'agree'],
['mid', 'no', 'yes', '3', 'agree'],
['elder', 'no', 'yes', '3', 'agree'],
['elder', 'no', 'yes', '2', 'agree'],
['elder', 'yes', 'no', '2', 'agree'],
['elder', 'yes', 'no', '3', 'agree'],
['elder', 'no', 'no', 1, 'refuse'],
]
#print(type(dataSet))
labels = ['age', 'working', 'house', 'credit_situation']
return dataSet, labels
下面我们来更直观的展示一下分类的结果
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="round", color='#3366FF') # 定义判断结点形态
leafNode = dict(boxstyle="circle", color='#FF6633') # 定义叶结点形态
arrow_args = dict(arrowstyle="<-", color='g') # 定义箭头
#计算叶子结点个数
def getNumLeafs(deTree):
numLeafs = 0
firstCondition = list(deTree.keys())[0]
secondDict = deTree[firstCondition]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':#测试结点的数据类型是否为字典
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs += 1
return numLeafs
#计算树的深度
def getTreeDepth(deTree):
maxDepth = 0
firstCondition = list(deTree.keys())[0]
secondDict = deTree[firstCondition]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth : maxDepth = thisDepth
return maxDepth
# 绘制带箭头的注释
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt,
xytext=centerPt, xycoords='axes fraction',
textcoords='axes fraction',va="center",
ha="center", bbox=nodeType, arrowprops=arrow_args )
# 在父子结点间填充文本信息
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center",
ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree) # 计算宽与高
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0]
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))
/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode) # 标记子结点属性值
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD # 减少y偏移
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key],
(plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree,
#and the first element will be another dict
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.show()
# 测试代码
if __name__ == "__main__":
dataSet, featLabels = createDataSet()
deTree = crtDecisionTree(dataSet, featLabels)
createPlot(deTree)
C4.5
C4.5算法使用信息增益比来选择属性,继承了ID3算法的优点,并在一下几个方面对ID3的算法进行改进:
克服了用信息增益选择属性时偏向选择取值多的属性的不足性;
在树构造过程中进行剪枝;
能够完成对连续属性的离散化处理;
能够对不完整数据进行处理。
在算法描述上,仅对上面ID3里的第三步中改为信息增益比即可
def chooseBestFeatSplitC45(dataSet):
'''
选择最好的数据集划分方式
dataSet:数据集
return:划分结果
'''
numFeatures = len(dataSet[0]) - 1
baseEnt = calcuInfoEnt(dataSet)
bestInfoGainRate = 0.0
bestFeature = -1
for i in range(numFeatures):
infoGainRate = calcuInfoGainRatio(dataSet, baseEnt, i) #计算信息增益比
if(infoGainRate > bestInfoGainRate):
bestInfoGainRate = infoGainRate
bestFeature = i
return bestFeature
然后我们考虑用分类好的决策树模型进行预测分类
def classify(inputTree, featLabels, testData):
'''
利用决策树进行分类
inputTree:构造好的决策树模型
featLabels:所有的特征标签
testData:测试数据
return:返回分类的决策结果
'''
firstCondition = list(inputTree.keys())[0]
secondDict = inputTree[firstCondition]
#拿到第一个分类条件在labels里面的索引
featIndex = featLabels.index(firstCondition)
featVal = testData[featIndex]
result = secondDict[featVal]
if isinstance(result, dict):
classLabel = classify(result, featLabels, testData)
else: classLabel = result
return classLabel
dataSet, featLabels = createDataSet()
deTree = crtDecisionTree(dataSet, featLabels)
print('预测结果是:' +
classify(deTree, featLabels, ['youth','no','yes',1]))
预测结果是:agree
CART(分类与回归树)
CART:分类与回归树,也是一种应用广泛的决策树学习方法。但是CART算法比较强大,既可以用来作分类树,也可以用来作回归树。在作为分类树的时候,与ID3,C4.5差别不是很大,只是选择特征的根据不同。在通常情况下,决策树是二叉树,也就是说它的特征值都是二分类的。当用CART作回归树时,以最小平方误差作为划分样本的依据。
在分类树中采用基尼指数用来选择最优特征。假设有 个类,样本点属于第 类的概率为 ,则概率的基尼指数定义为
对于给定样本集合 , 为样本个数, 是 中属于第 类的样本子集,则此时的基尼指数为
def calcuGini(dataSet):
'''
计算基尼指数
dataSet:数据集
return:基尼指数的计算结果
'''
numElements = len(dataSet)
Gini = 1.0
labelCounts = {}
for eleVec in dataSet: #遍历每个实例,统计标签的频数
curLabel = eleVec[-1]
if curLabel not in labelCounts.keys():
labelCounts[curLabel] = 0
labelCounts[curLabel] += 1
for key in labelCounts:
prob = float(labelCounts[key]) / numElements
Gini -= prob * prob
return Gini
那么在给定特征A的条件下,集合D的基尼指数定义为
因为特征的分类个数会决策树的分支个数,CART是二叉树,那么在给定特征A的时候,集合D就会被分为两类 和
基尼指数表示集合D的不确定性,和熵类似,当经过 的分类后, 的数值越大,样本集合的不确定性也就越大。
def calcuGiniBaseFeat(dataSet, featI, featVal):
'''
计算给定特征下的基尼指数
dataSet:数据集
featI:特征维度
featVal:特征维度下的特征值
return:计算结果
'''
D0 = []
D1 = []
for eleVec in dataSet:
if eleVec[featI] == featVal:
D0.append(eleVec)
else:
D1.append(eleVec)
Gini = float(len(D0)) / len(dataSet) * calcuGini(D0) + \
float(len(D1)) / len(dataSet) * calcuGini(D1)
return Gini
下面描述下CART分类树的算法步骤:
输入:训练数据集D,停止计算的条件
输出:CART决策树
根据训练数据集,从根结点开始,递归地对每个结点进行以下操作,构建二叉决策树
(1)设结点的训练数据集为 , 计算现有特征对该数据集的基尼指数。此时,对每一个特征 ,对其可能取的每个值 ,根据样本点对 的测试为“是”或“否”将 分割成 和 两部分,计算 时的基尼指数;
(2)在所哟可能的特征 以及它们所有可能的切分点 中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。依据最优特征和最优切分点,从现结点生成两个子结点,将训练集依特征分配到两个子结点中;
(3)对两个子结点递归地调用(1),(2),直至满足停止条件为止;
(4)生成CART决策树
算法停止计算的条件是结点中的样本个数小于预定阈值,或者样本集的基尼指数小于预定阈值(代表样本基本属于同一类),或者没有更多特征。
def chooseBestFeatSplitGini(dataSet):
bestGini = float("inf")
bestFeatI = 0
condiGini = 0.0
numFeatures = len(dataSet[0]) - 1
for i in range(numFeatures):
featList = [element[i] for element in dataSet]
featSet = set(featList)
for splitVal in featSet:
condiGini = calcuGiniBaseFeat(dataSet, i, splitVal)
if condiGini < bestGini:
bestFeatI = i
bestGini = condiGini
return bestFeatI
def crtDecisionTreeCART(dataSet, featLabels):
'''
创建决策树
dataSet:训练数据集
featLabels:所有特征标签
return:返回决策树字典
'''
classList = [element[-1] for element in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0] #所有的类标签都相同
if len(dataSet[0]) == 1:
return majorityClassify(classList) #用完所有特征
bestFeat = chooseBestFeatSplitGini(dataSet)
bestFeatLabel = featLabels[bestFeat]
deTree = {bestFeatLabel:{}}
subFeatLabels = featLabels[:] #复制所有类标签,保证每次递归调用时不改变原来的
del(subFeatLabels[bestFeat])
featValues = [element[bestFeat] for element in dataSet]
featValSet = set(featValues)
#####
for value in featValSet:
#subFeatLabels = featLabels[:]
deTree[bestFeatLabel][value] = \
crtDecisionTreeCART(splitDataSet(dataSet, bestFeat, value),
subFeatLabels)
return deTree
def createDataSetCART():
import numpy as np
dataSet = np.loadtxt("C:\\Users\\MAIBENBEN\\Desktop\\lenses.txt", dtype=str)
#print(type(dataSet))
labels = ['age', 'prescript', 'astigmatic', 'tearRate']
return dataSet.tolist(), labels
dataSet, featLabels = createDataSetCART()
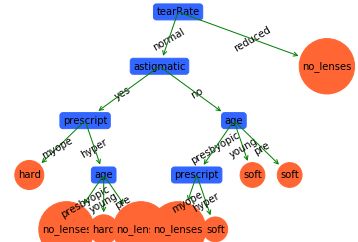
deTree = crtDecisionTreeCART(dataSet, featLabels)
createPlot(deTree)
这棵树看起来还是比较复杂的,我们可以测试一下它的泛化能力。
def calcuError(tree, testData, labels):
errCount = 0.0
for i in range(len(testData)):
if classify(tree, labels, testData[i]) != testData[i][-1]:
errCount += 1
return float(errCount)
testData = np.loadtxt("C:\\Users\\MAIBENBEN\\Desktop\\testData.txt", dtype=str)
dataSet, featLabels = createDataSetCART()
deTree = crtDecisionTreeCART(dataSet, featLabels)
testErr = calcuError(deTree, testData.tolist(), featLabels)
print(testErr)
0.0
通过上面的简单预测,我们的模型没有预测误差(谢天谢地,这是件好事)。不过当在更大的数据集训练得出的决策树中,树将会变得非常复杂,这大概率会造成过拟合的现象,即泛化能力就会差些。
所以我们有必要了解下决策树的剪枝。
pruning(剪枝)
在决策树学习中将已经生成的树进行简化的过程称为剪枝。决策树的剪枝往往通过极小化决策树的损失函数或代价函数来实现。实际上剪枝的过程就是一个动态规划的过程:从叶结点开始,自底向上的对内部结点计算预测误差以及剪枝后的预测误差,如果两者的预测误差是相等或剪枝后预测误差更小,那么就是剪掉的好。但如果剪枝后的预测误差更大,就不要剪了。剪枝后,原内部结点会变成新的叶结点,其决策类别由多数表决决定。不断重复上述的过程,直到预测误差最小为止。
实现代码如下:
import copy
def isTree(obj):
return (type(obj).__name__=='dict')
#计算剪枝后的预测误差
def calcuPruErr(major, testData):
errCount = 0.0
for i in range(len(testData)):
if major != testData[i][-1]:
errCount += 1
return float(errCount)
#对决策树进行剪枝
def pruningTree(inputTree, dataSet, testData, featLabels):
labels = featLabels[:]
firstFeat = list(inputTree.keys())[0]
secondDict = inputTree[firstFeat]
classList = [element[-1] for element in dataSet]
featIndex = labels.index(firstFeat)
subLabels = copy.deepcopy(labels)
del(labels[featIndex])
for key in list(secondDict.keys()):
if isTree(secondDict[key]):
#深度优先搜索,递归剪枝
#key是特征值
subDataSet = splitDataSet(dataSet, featIndex, key)
subTestSet = splitDataSet(testData, featIndex, key)
if len(subDataSet) > 0 and len(subTestSet) > 0:
inputTree[firstFeat][key] = \
pruningTree(secondDict[key],subDataSet,
subTestSet,copy.deepcopy(labels))
if calcuError(inputTree, testData, subLabels) < \
calcuPruErr(majorityClassify(classList), testData):
#剪枝后的误差反而变大,不做处理,直接返回
return inputTree
else:
#剪枝,原父结点变成子结点,其类别由多数表决决定
print(majorityClassify(classList))
return majorityClassify(classList)
newTree = pruningTree(deTree, dataSet, testData.tolist(), featLabels)
createPlot(newTree)
让我们来看下剪枝好的树的泛化能力
tErr = calcuError(newTree, testData.tolist(), featLabels)
print(tErr)
0.0
当然CART决策树还可以用来做回归任务,这里就不进行详细说明了。。。