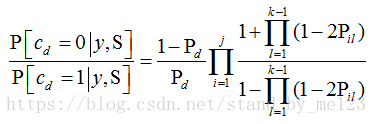LDPC码译码原理——概率公式推导
怎么说呢,一直以来都想写一下博客。近半年多来我一直在学习LDPC码译码上的东西,主要是在FPGA实现上的,所以这次想写一些关于这方面的内容,包括译码的原理、仿真以及实现。(当然是基于准循环LDPC码上实现的)
不过呢,我写这个的初衷是为了让初学者理解入门用的,而不是在大牛面前班门弄斧,有错误之处欢迎大家批评指正。
不知道会不会有人一开始像我一样,为了学好LDPC码,先去好好了解其它的诸如RS码或者是卷积码,把它们学到从入门到精通最后放弃。长些以往,坚持下来,再来看LDPC码你就会惊喜地发现之前学的其它码型的内容恰到好处地完美避开了你将所学的内容。是的,学习LDPC码,你并不需要其它类型码的先验知识,所以放心大胆地去学吧!
在我当下认知中,LDPC码译码的核心就是一切围绕着那个稀疏校验矩阵做周而复始、循环往复的打转。而该码型为啥倍受人们喜爱呢,原因就在于它是一个稀疏矩阵。这就好比当你拖着无比沉重的身躯行走在即将过零点的地铁中时,这时你突然发现整节车厢都是空的!随心所欲地躺在一排位置上,舒服!一个稀疏矩阵中的那些0值就好比车厢中的空位置,你可以跑到任意位置对它进行操作,也可以理都不理它,当然我们通常选择的是后者。下面先给大家附上我所用的校验矩阵,该矩阵是CCSDS提供的(8176,7154)码,行重32,列重4。
这里面,每一行数值为1的校验节点和所要判断的码字d组成一个校验方程,对于每一列亦是如此。
以下是分割线
=================================================================
=================================================================
好了,下面才是我今天主要想讲的内容——关于LDPC码译码的概率公式和公式中每个符号的含义。
所谓的译码过程,实则是一个概率计算的过程,好比说当下式的值大于1时那我们就会将输出值判决为1,and vice versa. 此公式就是我们整个LDPC译码的核心,下面我就先讲一讲每个符号的含义以及此公式的证明方法。
假设我们考虑接收到的码字为y,发送码字为c,S表示所发送的码字符合这j个校验方程的集合(我的理解是加上了这个约束条件相当于考虑了不同发送码字之间的相关性)。上式中![]() 表示在收到的数据为y时且满足校验方程约束条件下,码字被判断为0的概率。
表示在收到的数据为y时且满足校验方程约束条件下,码字被判断为0的概率。![]() 表示若每个发送码字独立不相关时收到的信息被判决为1的概率。
表示若每个发送码字独立不相关时收到的信息被判决为1的概率。![]() 表示对于包含判决码字d的第i个校验方程其第L个比特为1的概率。可以看出上式的主要作用就是将原本看似独立不相关的
表示对于包含判决码字d的第i个校验方程其第L个比特为1的概率。可以看出上式的主要作用就是将原本看似独立不相关的![]() 通过j个校验方程的修正,修正为
通过j个校验方程的修正,修正为![]() 这类具有相关性的概率,以此来降低误码率。
这类具有相关性的概率,以此来降低误码率。
看到这样一个复杂而又庞大的公式,不要怕,要像剥洋葱一样对待它~
我们先来证明以下引理:一个长为m的相互独立的二进制序列,其中第L个比特是1的概率为![]() ,那么整个序列中包含偶数个1的概率为
,那么整个序列中包含偶数个1的概率为
利用构造函数的方法,对于t的m次多项式 ,通过数学归纳法可证
,通过数学归纳法可证![]() 的系数为其序列中包含i个1的概率。
的系数为其序列中包含i个1的概率。
数学归纳法证明如下:
- 当m=1时,
 ,t的一次幂及零次幂显然即为包含1个1或0个1的概率。
,t的一次幂及零次幂显然即为包含1个1或0个1的概率。 - 假设当m=k时,
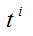 的系数
的系数 为k次多项式
为k次多项式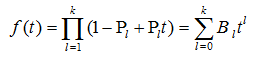 中包含i个1的概率。
中包含i个1的概率。 - 当m=k+1时,
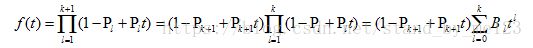 ,由上式可以求得
,由上式可以求得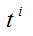 的系数为
的系数为 ,即为k+1次多项式中包含i个1的概率。(两边极端情况显然成立,此次不再累述)
,即为k+1次多项式中包含i个1的概率。(两边极端情况显然成立,此次不再累述)
综上,对于t的m次多项式 ,
,![]() 的系数为其序列中包含i个1的概率。
的系数为其序列中包含i个1的概率。
同理,对于多项式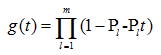 ,它与f(t)的差异仅仅在于奇次幂系数为负值。因此,我们可以通过f(t)和g(t)的相加来消去奇次项, 并令t=1。从而得到
,它与f(t)的差异仅仅在于奇次幂系数为负值。因此,我们可以通过f(t)和g(t)的相加来消去奇次项, 并令t=1。从而得到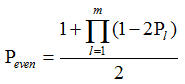 ,
, 。
。
由此根据引理以及条件概率公式,我们可以得到
在上式![]() 中,当
中,当![]() 时,只有当剩余的k-1个比特含有偶数个1才能使得相应的校验方程成立。即
时,只有当剩余的k-1个比特含有偶数个1才能使得相应的校验方程成立。即
同理,可得
由此,我们可以得到最初的公式
关于LDPC码译码的概率公式就先推导到这啦,下次再和大家讲如何从上述公式推演出BP算法以及在工程中如何 希进行初始化的。另外希望大家看了后能留下宝贵的建议,我也好努力往更好的方向发展。