有时候,我们解决一个很庞大的问题的时候,不知道该如何下手。其实往往很庞大的问题,都会有一些规律可循,我们可以将这个庞大的问题分解分解再分解,降维降维再降维,最终大事化小,(小事我们知道该怎么解决)于是乎小事化了,最终的结果是,解决了一件小事,就解决了整件大事。
快速排序就是利用这种“大事化小,小事化了”的思想来解决排序问题的。
欧几里得算法(辗转相除法)
我们在小学数学的时候,遇到过一个问题:求两个数的最大公约数。求最大公约数就是求同时都能被两个数整除的最大的一个数。比如 12 和 6 的最大公约数就是 6。
按照欧几里得算法,我们可以怎么样求得两个数的最大公约数呢?
举个栗子(来源于百度百科):求 123456 和 7890 的最大公约数。
- (1)两个数中 最小 的数是 7890,我们记录下来,然后用大的数除以小的数:
123456 ÷ 7890 = 15 ······ (余数) 5106 - (2)此时我们拿到上个式子中的被除数(小的那个数) 7890 以及余数 5106,我们用大的这个数 7890 除以小的数 5106 (余数肯定要比被除数大):
7890 ÷ 5106 = 1 ······ (余数) 2784 - (3) 重复上面的过程:
5106 ÷ 2784 = 1 ······ (余数) 2322
2784 ÷ 2322 = 1 ······ (余数) 462
2322 ÷ 462 = 5 ······ (余数) 12
462 ÷ 12 = 38 ······ (余数) 6
12 ÷ 6 = 2 ······(余数) 0
好,此时通过反复(辗转)的被除数变为除数,余数变为被除数,我们已经把此时的余数变为了 0,0 是辗转相除的终点站,一旦余数为 0 我们就结束计算,此时,最后一个式子中的被除数 6 就是我们要求解的 最大公约数 !
我们来看这个计算最大公约数的过程,其实它所干的一件事情就是把大事化小,小事化了。
最开始,我们计算 123456 和 7890 的最大公约数,发现,并不能直接的看出来;
于是乎我们进行了一步除法,把问题的 规模缩小 ,转变成了求 7890 和 5160 的最大公约数的问题(为什么呢?来自 欧几里得算法的证明))。发现还是不能直接看出来;
于是我们再次进行除法,再次把问题 规模缩小 ,把问题转换成了求 5160 和 2784 的最大公约数的问题;
··· ···
最终我们把问题转换成了求 12 和 6 的最大公约数的问题,显然,最大公约数是 6。
当然,欧几里得算法的证明过程我们有兴趣可以看,没有兴趣就可以不看,但是它用的这个思想,却是解决问题的核心——大事化小,小事化了,大事小事之间有所关联,知道小事怎么解决,就解决了大事 。
快速排序
算法过程
快速排序的过程,也是这样一个化繁为简,化不知为已知的过程。什么样的队列是绝对有序的呢?答案是空队列,或者只有一个元素的队列。
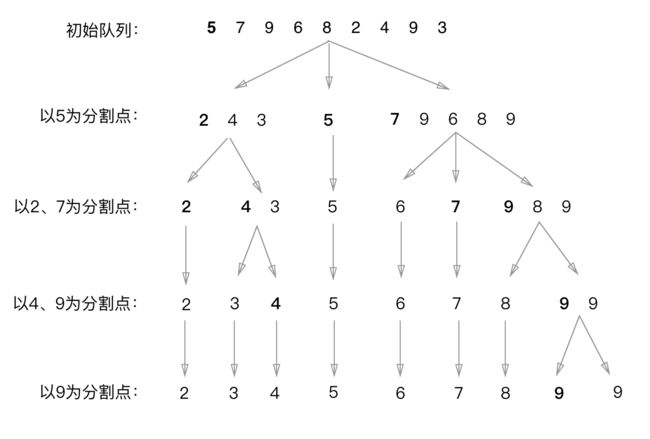
快速排序的核心是,找一个队列中的值作为分割值,用这个值把整个队列分成左右两部分,左边的部分都比这个分割值小,右边的部分都比这个分割值大,如果我们可以让左边的部分全部有序,让右边的部分也全部有序,那么最终我们的序列就是 【左边的队列】 + 【分割值】+ 【右边的队列】,那么我们整个队列就都有序了。这个过程就是把最初始的大的队列排序问题变成了左右两个小队列的排序问题,问题规模相应的减小了,最多甚至会减小一半!如果我们再次分割呢?左边的部分再找到一个分割值,把左边的部分分成两部分,右边的部分也找到一个分割值,把右边的部分也分成了两部分,那么问题的规模是不是又减小成了四个小队列的排序问题呢?我们继续分下去,直到分割成了队列元素是1个的时候,这个时候所有组成最终队列的小队列们都是有序的,那么依次合并,最终的队列就是有序的!
当我们每次都把队列的第一个元素当做分割值的时候,过程就如图中,每一步的结果都是以子队列的第一个元素为分割点进行分割,把队列分割成左边比分割点小,右边比分割点大的队列们的整体情况:
这样我们得到的所有子队列的加和,最终就是个有序的队列。
算法实现
- 不考虑空间占用的情况(开辟临时空间存储)
#coding:utf-8
import numpy as np
def quick_sort(data):
if len(data) < 2:
return data
copy_data = list(data)
# 分割点最简单的就是取第一个数
break_point = copy_data[0]
# 比分割点小的数,都放在一起
# 注意:这里会额外占用内存空间
smaller_data = [i for i in copy_data[1:] if i < break_point]
# 比分割点大的数,都放在一起
# 注意:这里会额外占用内存空间
bigger_data = [i for i in copy_data[1:] if i > break_point]
# 此时break_point本身是有序的,因为只有它自己一个元素
# 我们只要让比break_point小的所有数都有序,让比break_point大的所有数也有序(递归调用)
# 最终的结果就是由三部分组成:
# [小于break_point的所有数的有序序列] [break_point] [大于break_point的所有数的有序序列]
return quick_sort(smaller_data) + [break_point] + quick_sort(bigger_data)
array = np.arange(20)
np.random.shuffle(array)
print('输入的数据: {}'.format(list(array)))
sorted_array = quick_sort(array)
print('排序之后的数据:{}'.format(sorted_array))
结果是:
- 不产生额外空间占用(就地排序)
#coding:utf-8
import numpy as np
# 就地快速排序
def quick_sort_inplace(data):
if len(data) < 2:
return
quick_sort_content(data, 0, len(data)-1)
# 获取中间的break_point所在位置,并且根据这个位置分割数组递归分别进行排序
def quick_sort_content(data, f, t):
if f >= t:
return
break_point = get_break_point(data, f, t)
quick_sort_content(data, f, break_point)
quick_sort_content(data, break_point+1, t)
# 获取中间break_point的位置
def get_break_point(data, f, t):
value = data[f]
i = t
for j in range(t, f, -1):
if data[j] > value:
data[i], data[j] = data[j], data[i]
i -= 1
data[f], data[i] = data[i], data[f]
return i
array = np.arange(20)
np.random.shuffle(array)
array = list(array)
print('输入的数据: {}'.format(array)) # 排序后原数组内容顺序变了,但是内存空间没有变化
quick_sort_no_other_space(array)
print('排序之后的数据:{}'.format(array)) # 排序后原数组内容顺序变了,但是内存空间没有变化
结果是:
上一篇:写给媳妇儿的算法(五)——插入排序
下一篇:写给媳妇儿的算法(七)——归并排序