技术交流QQ群:1027579432,欢迎你的加入!
使用Apriori算法进行关联分析(层次聚类)
一、基础知识
- 1.关联分析定义及存在的问题
- 定义:从大规模的数据集中寻找物品间的隐含关系,被称为关联分析或关联规则学习。
- 关联分析存在的主要问题:主要问题在于寻找不同物品的组合是一项很耗时的任务,所需要的计算代价很高,暴力方法无法解决这个问题,所以使用更加合理的方法在合理的时间范围内找到频繁项集。
- 2.Apriori算法的优缺点及适用场合
- 优点:容易编码实现
- 缺点:在大数据集上可能较慢
- 适用场合:数值型或标称型数据
- 3.关联分析中的基本概念
- 关联分析是一种在大规模数据集上寻找有趣关系的任务。这些关系可以有两种形式来表示,频繁项集和关联规则。
- 频繁项集:经常出现在一块的物品的集合。
- 关联规则:暗示两种物品之间可能存在很强的关系。
- 4.频繁项集和关联规则的解释
- 5.频繁的定义
- 何谓有趣关系?有什么来定义有趣?当寻找频繁项集时,频繁的定义是什么?可以使用支持度和可信度来描述频繁。
- 一个项集的支持度:数据集中包含该项集的记录所占有的比例。例如,上例中{豆奶}的支持度是4/5,{豆奶,尿布}的支持度是3/5。支持度是针对项集来说的,因此可以定义一个最小支持度,而只保留满足最小支持度的项集。
- 一条关联规则的可信度/置信度:是针对某条关联规则来定义的。例如,上例中像关联规则{尿布}->{葡萄酒}这条关联规则的可信度被定义为支持度({尿布,葡萄酒}})=3/5 / 支持度({尿布})=4/5,可知尿布->葡萄酒的可信度是0.75,这意味着,对于包含所有尿布的记录,我们的规则对其中的75%都是适用的。
二、Apriori算法原理
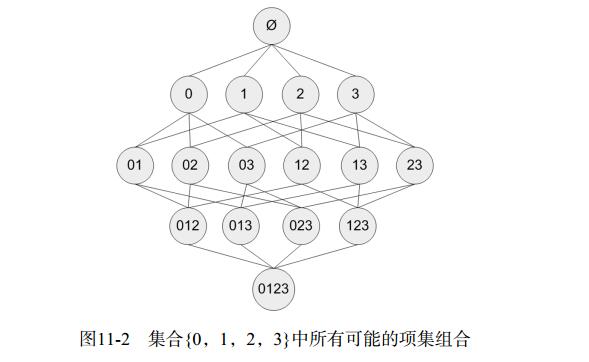
- 假设经营一家商店,商品的种类并不多。我们的目标是找出顾客经常一起购买的商品集合,目前只有四种商品,即0,1,2,3。?表示空集集不包括任何商品的集合。商品集合之间的连线表示两个或更多集合可以组合成一个更大的集合。
- 上面我们说过,使用支持度来表示频繁的定义。因此,一个集合的支持度表示为有多少比例的记录包含该集合。例如,给定集合{0,3},如何计算其支持度?我们首先遍历,每条记录并检查此记录是否同时包含0和3,如果同时包含了这两个商品,则就增加计数值。在扫描完所有的数据后,使用统计得到的总数除以总的记录数目,就可以得到支持度。
- 存在的问题:上面只是针对单个集合{0,3},要获得每种可能集合的支持度就需要多次重复上述过程。根据下图,可以发现,仅有4种商品的集合,也需要遍历数据15次。随着商品种类的增加,遍历次数就会剧烈增加。对于包含N种商品的数据集,一共有2^N-1种项集的组合。需要很长的时间才能计算完。
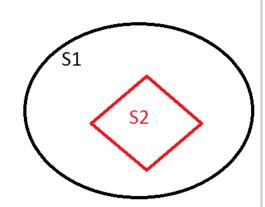
- 超集:如果集合S2中每个元素都在集合S1中,而且集合S1中可能包含集合S2中没有的元素,则集合S1是S2的一个超集,集合S2是S1的子集。
- 为了降低所需的计算时间,使用Apriori算法可以减少感兴趣的项集。Apriori原理:如果某个项集是频繁的,那么它的所有子集也是频繁的。例如,集合{0,1}是频繁的,那么{0}、{1}也一定是频繁的。即如果一个项集的非频繁集,它的所有超集也是非频繁的。例如下图中已知集合{2,3}是非频繁的,则它的超集{0, 2, 3}、{1, 2, 3}、{0, 1, 2, 3}也是非频繁的。也就是说,一旦计算出了{2, 3}的支持度,知道它是非频繁的,就不需要计算集合{0, 2, 3}、{1, 2, 3}、{0, 1, 2, 3}的支持度。使用Apriori原理就可以避免项集数目的指数增长,从而在合理的时间内计算出频繁集。
三、使用Apriori算法来发现频繁集
- 1.关联分析的目标是两个:发现频繁集和发现关联规则。首先需要找到频繁项集,然后才能获得关联规则。
- 2.Apriori算法发现频繁集的步骤:Apriori算法的两个输入参数分别是最小支持度、数据集。首先会生成所有单个物品的项集列表;接着扫描记录来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉。然后,对剩下的集合进行组合来生成包含两个元素的项集。接着,在重新扫描记录,去掉不满足最小支持度的项集。该过程重复进行,直到所有项集都被去掉。具体代码如下:
- 加载数据集
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
- 构建集合C1,C1是大小为1的所有候选项集的集合,如{{1},{2},{3},{4},{5}}
def createC1(dataSet):
C1 = []
for record in dataSet:
for item in record:
if not [item] in C1:
C1.append([item])
C1.sort()
return list(map(frozenset, C1)) # frozenset是对C1进行冰冻,使C1不能进行修改
- 从C1中生成L1(L1是满足最小支持度的要求的项集构成的集合)
def scanD(D, Ck, minSupport):
"""
D:数据集
Ck:候选项集列表
minSupport:感兴趣项集的最小支持度
返回值:retList---L1;supportData---包含支持度值的字典
"""
ssCnt = {} # 创建一个空字典,字典的key就是C1中的集合,value是C1中的集合在所有记录中出现的次数
for record in D: # 遍历数据集中的每条记录
for can in Ck: # 遍历C1中的所有候选项集
if can.issubset(record): # 如果C1中的集合是记录中的一部分,则增加字典中对应的计数值;
if not can in ssCnt:
ssCnt[can] = 1 # 字典的key就是集合
else:
ssCnt[can] += 1
numItems = float(len(D)) # 总的样本数
print("总的记录数:", numItems)
retList = [] # 创建一个空列表,此列表包含满足最小支持度的集合
supportData = {} # 最频繁项集的支持度
for key in ssCnt: # 遍历字典中的每个元素,并计算其最小支持度
support = ssCnt[key] / numItems # 计算支持度
if support >= minSupport: # 如果C1中的支持度满足最小支持度的要求,就将字典中的元素加入retList中
retList.insert(0, key) # 在列表的首部插入新的集合
supportData[key] = support # 最频繁项集的支持度
return retList, supportData
- 进行合并操作,创建候选项集Ck
def aprioriGen(Lk, k): # 创建候选项集Ck,对L1中的元素两两组合,得出候选项集C2
"""
频繁项集列表LK,项集元素个数K
"""
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i + 1, lenLk):
L1 = list(Lk[i])[:k - 2]
L2 = list(Lk[j])[:k - 2]
L1.sort()
L2.sort()
if L1 == L2:
retList.append(Lk[i] | Lk[j]) # 集合的并操作
return retList
- Apriori核心程序
def apriori(dataSet, minSupport=0.5):
C1 = createC1(dataSet)
D = list(map(set, dataSet))
L1, supportData0 = scanD(D, C1, minSupport)
L = [L1]
k = 2
while(len(L[k - 2]) > 0):
Ck = aprioriGen(L[k - 2], k)
Lk, supportDatak = scanD(D, Ck, minSupport)
supportData0.update(supportDatak)
L.append(Lk)
k += 1
return L, supportData0
- 3.从频繁项集中挖掘关联规则
- 从频繁项集中挖掘关联规则的步骤:首先从一个频繁项集开始,创建一个关联规则表,每条关联规则的右部只含有一个元素。然后,对这些关联规则进行测试,如果每条关联规则的可信度不满足最小的可信度minConf要求,就去掉此条关联规则。最后,合并剩余的关联规则,创建一个新的关联规则表,其中关联规则的右部包含两个元素。重复上面的步骤,直到关联规则表为空时停止。具体代码如下:
- 关联规则表的生成
def generateRules(L, supportData, minConf=0.7):
"""
L:频繁项集
supportData:包含那些频繁项集支持数据的字典
minConf:最小的可信度
返回:一个包含可信度的规则列表bigRuleList
"""
bigRuleList = [] # 初始化存放所有关联规则的列表
for i in range(1, len(L)):
for freqSet in L[i]: # 最开始的关联规则表中,每条关联规则freqSet的右部H1只有一个元素
H1 = [frozenset([item]) for item in freqSet]
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
- 可信度的计算,例如存在一条关联规则{0,1,2}-->{3, 5},则可信度的计算为:{0,1,2,3,5}的支持度 / {0,1,2}的支持度。其中下面程序中freqSet就是集合{0,1,2,3,5};H就是集合{3, 5};conseq就是{3}、{5}
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
prunedH = []
for conseq in H:
conf = supportData[freqSet] / supportData[freqSet - conseq] # 计算每条关联规则的可信度
print(freqSet - conseq, '--->', conseq, '可信度conf:', conf)
brl.append((freqSet - conseq, conseq, conf))
prunedH.append(conseq)
return prunedH # 返回一个满足最小可信度要求的关联规则表
- 合并上一次生成的关联规则,生成新的候选关联规则列表
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
m = len(H[0])
if (len(freqSet) > (m + 1)): # 合并关联规则
Hmp1 = aprioriGen(H, m + 1) # 创建新的频繁项集
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
if (len(Hmp1) > 1): # 新的关联规则表中,每条关联规则中的右边Hmp1必须包含两个元素
rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
- 打印关联规则
# 打印关联规则
def pntRules(ruleList, itemMeaning):
for ruleTup in ruleList:
for item in ruleTup[0]:
print(itemMeaning[item])
print(" -------->")
for item in ruleTup[1]:
print(itemMeaning[item])
print("可信度: %f" % ruleTup[2])
四.所有代码如下:
```
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2019-05-18 11:30:01
# @Author : cdl ([email protected])
# @Link : https://github.com/cdlwhm1217096231/python3_spider
# @Version : $Id$
from numpy import *
# 层次聚类,基于查找关联规则Apriori算法
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
# 构建集合C1,C1是大小为1的所有候选项集的集合,如{{1},{2},{3},{4},{5}}
def createC1(dataSet):
C1 = []
for record in dataSet:
for item in record:
if not [item] in C1:
C1.append([item])
C1.sort()
return list(map(frozenset, C1)) # frozenset是对C1进行冰冻,使C1不能进行修改
# 从C1中生成L1(L1是满足最小支持度的要求的项集构成的集合)
def scanD(D, Ck, minSupport):
"""
D:数据集
Ck:候选项集列表
minSupport:感兴趣项集的最小支持度
返回值:retList---L1;supportData---包含支持度值的字典
"""
ssCnt = {} # 创建一个空字典,字典的key就是C1中的集合,value是C1中的集合在所有记录中出现的次数
for record in D: # 遍历数据集中的每条记录
for can in Ck: # 遍历C1中的所有候选项集
if can.issubset(record): # 如果C1中的集合是记录中的一部分,则增加字典中对应的计数值;
if not can in ssCnt:
ssCnt[can] = 1 # 字典的key就是集合
else:
ssCnt[can] += 1
numItems = float(len(D)) # 总的样本数
print("总的记录数:", numItems)
retList = [] # 创建一个空列表,此列表包含满足最小支持度的集合
supportData = {} # 最频繁项集的支持度
for key in ssCnt: # 遍历字典中的每个元素,并计算其最小支持度
support = ssCnt[key] / numItems # 计算支持度
if support >= minSupport: # 如果C1中的支持度满足最小支持度的要求,就将字典中的元素加入retList中
retList.insert(0, key) # 在列表的首部插入新的集合
supportData[key] = support # 最频繁项集的支持度
return retList, supportData
#
def aprioriGen(Lk, k): # 创建候选项集Ck,对L1中的元素两两组合,得出候选项集C2
"""
频繁项集列表LK,项集元素个数K
"""
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i + 1, lenLk):
L1 = list(Lk[i])[:k - 2]
L2 = list(Lk[j])[:k - 2]
L1.sort()
L2.sort()
if L1 == L2:
retList.append(Lk[i] | Lk[j]) # 集合的并操作
return retList
# Apriori核心程序
def apriori(dataSet, minSupport=0.5):
C1 = createC1(dataSet)
D = list(map(set, dataSet))
L1, supportData0 = scanD(D, C1, minSupport)
L = [L1]
k = 2
while(len(L[k - 2]) > 0):
Ck = aprioriGen(L[k - 2], k)
Lk, supportDatak = scanD(D, Ck, minSupport)
supportData0.update(supportDatak)
L.append(Lk)
k += 1
return L, supportData0
# 关联规则表的生成
def generateRules(L, supportData, minConf=0.7):
"""
L:频繁项集
supportData:包含那些频繁项集支持数据的字典
minConf:最小的可信度
返回:一个包含可信度的规则列表bigRuleList
"""
bigRuleList = [] # 初始化存放所有关联规则的列表
for i in range(1, len(L)):
for freqSet in L[i]: # 最开始的关联规则表中,每条关联规则freqSet的右部H1只有一个元素
H1 = [frozenset([item]) for item in freqSet]
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
# 计算可信度
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
prunedH = []
for conseq in H:
conf = supportData[freqSet] / supportData[freqSet - conseq] # 计算每条关联规则的可信度
print(freqSet - conseq, '--->', conseq, '可信度conf:', conf)
brl.append((freqSet - conseq, conseq, conf))
prunedH.append(conseq)
return prunedH # 返回一个满足最小可信度要求的关联规则表
# 合并上一次生成的关联规则,生成新的候选关联规则列表
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
m = len(H[0])
if (len(freqSet) > (m + 1)): # 合并关联规则
Hmp1 = aprioriGen(H, m + 1) # 创建新的频繁项集
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
if (len(Hmp1) > 1): # 新的关联规则表中,每条关联规则中的右边Hmp1必须包含两个元素
rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
# 打印关联规则
def pntRules(ruleList, itemMeaning):
for ruleTup in ruleList:
for item in ruleTup[0]:
print(itemMeaning[item])
print(" -------->")
for item in ruleTup[1]:
print(itemMeaning[item])
print("可信度: %f" % ruleTup[2])
if __name__ == "__main__":
dataSet = loadDataSet()
C1 = createC1(dataSet) # 原始集合C1
print("原始集合C1:", C1)
D = list(map(set, dataSet))
print("数据集D:", D)
L1, supportData0 = scanD(D, C1, minSupport=0.5)
print("频繁项集L1:", L1, "\n支持度:", supportData0)
print("---------------完整测试-----------------")
dataSet = loadDataSet()
L, supportData = apriori(dataSet)
print("频繁项集L:", L, "\n支持度: ", supportData)
print('--------------关联规则的生成-------------')
rules = generateRules(L, supportData, minConf=0.5)
print("关联规则为:", rules)
```