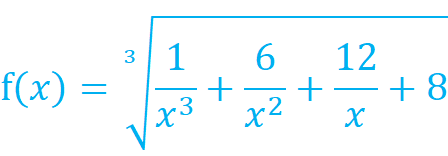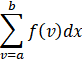数模中常用到的Matlab符号运算
一、 符号运算
符号对象的建立：sym 和 syms
sym 函数用来建立单个符号变量，一般调用格式为：符号变量 = sym(A) 参数 A 可以是一个数或数值矩阵，也可以是字符串
例如：
a=sym('a') a 是符号变量
b=sym(1/3） b 是符号常量
C=sym('[1 ab; c d]') C 是符号矩阵syms 命令用来建立多个符号变量，一般调用格式为：
syms 符号变量1 符号变量2 ... 符号变量n
syms a b c； 等价
>> a=sym('a');
>> b=sym('b');
>> c=sym('c');建立符号表达式通常有以下2种方法：
(1) 用 sym 函数直接建立符号表达式。
(2) 使用已经定义的符号变量组成符号表达式。
例如：
y=sym('sin(x)+cos(x)')
>> x=sym('x');
>> y=sin(x)+cos(x)
>> syms x;
>> y=sin(x)+cos(x)符号表达式的替换
用给定的数据替换符号表达式中的指定的符号变量
subs(f,x,a)
用 a 替换字符函数 f 中的字符变量 x
a 是可以是 数/数值变量/表达式 或 字符变量/表达式
若 x 是一个由多个字符变量组成的数组或矩阵，
则 a 应该具有与 x 相同的形状的数组或矩阵。
>> f=sym('2*u');
>> subs(f,'u',2)
>> f2=subs(f,'u','u+2')
>> a=3;
>> subs(f2,'u',a+2)
>> subs(f2,'u','a+2')
>> syms x y
>> f3=subs(f,'u',x+y)
>> subs(f3,[x,y],[1,2])符号矩阵
使用 sym 函数直接生成
>> A=sym('[1+x, sin(x); 5, exp(x)]')将数值矩阵转化成符号矩阵
>> B=[2/3, sqrt(2); 5.2, log(3)];
>> C=sym(B)符号矩阵中元素的引用和修改
>> A=sym('[1+x, sin(x); 5, exp(x)]');
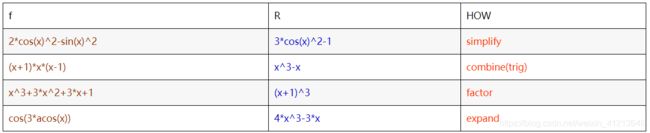
>> A(1,2) % 引用因式分解
factor（） 也可用于正整数的分解
>> factor(sym('12345678901234567890')) %大整数的分解要转化成符号常量函数展开
expand(f) %多项式展开
>> syms x; f=(x+1)^6;
>> expand(f)三角函数展开
>> syms x y; f=sin(x+y);
>> expand(f)合并同类项
collect(f,v): 按指定变量 v 进行合并
collect(f): 按默认变量进行合并
syms x y;
>> f= x^2*y + y*x - x^2 + 2*x ;
>> collect(f)
>> collect(f,y)函数简化
y=simple(f): 对 f 尝试多种不同的算法进行简化，返回其中最简短的形式
[How,y]=simple(f): y 为 f 的最简短形式，How 中记录的为简化过程中使用的方法。
y=simplify(f): 对 f 进行简化
>> syms x; f=sin(x)^2 + cos(x)^2 ;
>> simplify(f)
>> syms c alpha beta;
>> f=exp(c*log(sqrt(alpha+beta)));
>> simplify(f)此公式可如下处理
例：简化
>> syms x;
>> f=(1/x^3+6/x^2+12/x+8)^(1/3);
>> y1=simplify(f)
g1=simple(f)
>> g2=simple(g1) % 多次使用 simple 可以达到最简表达。分式通分
[N,D]=numden(f):
N 为通分后的分子，D 为通分后的分母
>> syms x y;
>> f=x/y+y/x;
>> [N,D]=numden(f)
>> [n,d]=numden(sym(112/1024))horner 多项式
horner 多项式：嵌套形式的多项式
列：
>> syms x;
>> f=x^4+2*x^3+4*x^2+x+1;
>> g=horner(f)计算导数
g=diff(f,v)：求符号表达式 f 关于 v 的导数
g=diff(f)：求符号表达式 f 关于默认变量的导数
g=diff(f,v,n)：求 f 关于 v 的 n 阶导数
>> syms x;
>> f=sin(x)+3*x^2;
>> g=diff(f,x)计算积分
int(f,v,a,b): 计算定积分 
int(f,a,b): 计算关于默认变量的定积分
int(f,v): 计算不定积分
int(f): 计算关于默认变量的不定积分
例：计算
和
>> syms x; f=(x^2+1)/(x^2-2*x+2)^2;
>> I=int(f,x)
>> K=int(exp(-x^2),x,0,inf)符号求和
symsum(f,v,a,b): 求和 
symsum(f,a,b): 关于默认变量求和
例：计算级数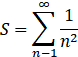
及其前100项的部分和
>> syms n; f=1/n^2;
>> S=symsum(f,n,1,inf)
>> S100=symsum(f,n,1,100)微分方程求解
dsolve
y=dsolve('eq1','eq2', ... ,'cond1','cond2', ... ,'v')
其中 y 为输出的解， eq1、eq2、. . . 为微分方程，
cond1、cond2、...为初值条件， v 为自变量
例 1：求微分方程
的通解，并验证。
>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x')
>> y= C2*exp(-x^2) + (x^2*exp(-x^2))/2例2：求微分方程
满足初值条件
的特解，并画出解函数的图形
>> y=dsolve('x*Dy+y-exp(x)=0', ...
'y(1)=2*exp(1)', 'x')
>> ezplot(y);
例3：求微分方程组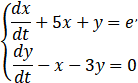
在初值条件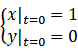 
下的特解，并画出解函数的图形。
[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0', ...
'x(0)=1', 'y(0)=0', 't')
ezplot(x,y,[0,1.3]);另外本人还开设了个人公众号：JiandaoStudio ，会在公众号内定期发布行业信息，以及各类免费代码、书籍、大师课程资源。
扫码关注本人微信公众号，有惊喜奥！公众号每天定时发送精致文章！回复关键词可获得海量各类编程开发学习资料！
例如：想获得Python入门至精通学习资料，请回复关键词Python即可。