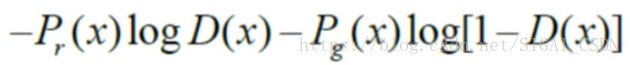生成式对抗网络模型综述

其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》，清华大学出版社，雷明著，由SIGAI公众号作者倾力打造。

• 书的购买链接
• 书的勘误，优化，源代码资源

引言

近年来，人工智能与深度学习已经成为耳熟能详的名词。一般而言，深度学习模型可以分为判别式模型与生成式模型。由于反向传播（Back propagation, BP）、Dropout等算法的发明，判别式模型得到了迅速发展。然而，由于生成式模型建模较为困难，因此发展缓慢，直到近年来最成功的生成模型——生成式对抗网络的发明，这一领域才焕发新的生机。

生成式对抗网络（Generative adversarial network, GAN）自Ian Goodfellow[1]等人提出后，就越来越受到学术界和工业界的重视。而随着GAN在理论与模型上的高速发展，它在计算机视觉、自然语言处理、人机交互等领域有着越来越深入的应用，并不断向着其它领域继续延伸。因此，本文将对GAN的理论与其应用做一个总结与介绍。

 

GAN的基本思想

GAN受博弈论中的零和博弈启发，将生成问题视作判别器和生成器这两个网络的对抗和博弈：生成器从给定噪声中（一般是指均匀分布或者正态分布）产生合成数据，判别器分辨生成器的的输出和真实数据。前者试图产生更接近真实的数据，相应地，后者试图更完美地分辨真实数据与生成数据。由此，两个网络在对抗中进步，在进步后继续对抗，由生成式网络得的数据也就越来越完美，逼近真实数据，从而可以生成想要得到的数据（图片、序列、视频等）。

如果将真实数据和生成数据服从两个分布，那么如图所示

蓝色分布为生成分布，绿色分布为真实分布，D为判别器，GAN从概率分布的角度来看，就是通过D来将生成分布推向真实分布，紧接着再优化D，直至到达图1(d)所示，到达Nash均衡点，从而生成分布与真实分布重叠，生成极为接近真实分布的数据。

 

GAN的基本模型

设z为随机噪声，x为真实数据，生成式网络和判别式网络可以分别用G和D表示，其中D可以看作一个二分类器，那么采用交叉熵表示，可以写作:

其中第一项的logD(x)表示判别器对真实数据的判断，第二项log(1 − D(G(z)))表示则对数据的合成与判断。通过这样一个极大极小(Max-min)博弈，循环交替地分别优化G和D来训练所需要的生成式网络与判别式网络，直到到达Nash均衡点。

 

GAN与Jensen-Shannon散度

对于原目标函数，在生成器G固定参数时，可以得到最优的判别器D。对于一个具体的样本，它可能来自真实分布也可能来自生成分布，因此它对判别器损失函数的贡献是：

其中  为真实分布，  为生成分布。令上式关于D(x)的导数为0，可以得到D(x)的全局最优解为：

对于gan 的生成器的优化函数可以写成：

将最优判别器代入，可以得到生成器的优化函数为：

此处简单回顾一下JS散度与KL散度：

显然，(1)式与JS散度形式相似，可以转换成：

综上，可以认为，当判别器过优时，生成器的loss可以近似等价于优化真实分布与生成器产生数据分布的JS散度。

 

生成器与判别器的网络

Ian在2014年提出的朴素GAN在生成器和判别器在结构上是通过以多层全连接网络为主体的多层感知机(Multi-layer Perceptron, MLP) 实现的，然而其调参难度较大，训练失败相当常见，生成图片质量也相当不佳，尤其是对较复杂的数据集而言。

由于卷积神经网络(Convolutional neural network, CNN)比MLP有更强的拟合与表达能力，并在判别式模型中取得了很大的成果。因此，Alec等人[2]将CNN引入生成器和判别器，称作深度卷积对抗神经网络（Deep Convolutional GAN, DCGAN）。图2为DCGAN生成器结构图。本质上，DCGAN是在GAN的基础上提出了一种训练架构，并对其做了训练指导，比如几乎完全用卷积层取代了全连接层，去掉池化层，采用批标准化(Batch Normalization, BN)等技术，将判别模型的发展成果引入到了生成模型中。此外，[2]还并强调了隐藏层分析和可视化计数对GAN训练的重要性和指导作用。

DCGAN虽然没有带来理论上以及GAN上的解释性，但是其强大的图片生成效果吸引了更多的研究者关注GAN，证明了其可行性并提供了经验，给后来的研究者提供了神经网络结构的参考。此外，DCGAN的网络结构也可以作为基础架构，用以评价不同目标函数的GAN，让不同的GAN得以进行优劣比较。DCGAN的出现极大增强了GAN的数据生成质量。而如何提高生成数据的质量（如生成图片的质量）也是如今GAN研究的热门话题。

GAN的模型改进

然而，GAN自从2014年提出以来，就存在着训练困难、不易收敛、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题。从那时起，很多研究人员就在尝试解决，并提出了改进方案，切实解决了部分问题，如生成器梯度消失导致的训练困难。当然也还有很多问题亟待解决，如生成样本的评价指标问题。本文将简单阐述几个较为突出的的改进措施。

 

WGAN

与前文的DCGAN不同，WGAN(Wasserstein GAN)并不是从判别器与生成器的网络构架上去进行改进，而是从目标函数的角度出发来提高模型的表现[3]。Martin Arjovsky等人先阐述了朴素GAN因生成器梯度消失而训练失败的原因[4]：他们认为，朴素GAN的目标函数在本质上可以等价于优化真实分布与生成分布的Jensen-Shannon散度。而根据Jensen-Shannon散度的特性，当两个分布间互不重叠时，其值会趋向于一个常数，这也就是梯度消失的原因。此外，Martin Arjovsky等人认为，当真实分布与生成分布是高维空间上的低维流形时，两者重叠部分的测度为0的概率为1，这也就是朴素GAN调参困难且训练容易失败的原因之一。

针对这种现象，Martin Arjovsky等人利用Wasserstein-1距离（又称Earth Mover距离）来替代朴素GAN所代表的Jensen-Shannon散度[3]。Wasserstein距离是从最优运输理论中的Kantorovich问题衍生而来的，可以如下定义真实分布与生成分布的Wasserstein-1距离：

其中,分别为真实分布与生成分布，  为,分的联合分布。相较于Jensen-Shannon散度，Wasserstein-1距离的优点在于，即使,互不重叠，Wasserstein距离依旧可以清楚地反应出两个分布的距离。为了与GAN相结合，将其转换成对偶形式:

从表示GAN的角度理解，fw表示判别器，与之前的D不同的是，WGAN不再需要将判别器当作0-1分类将其值限定在[0,1]之间，fw越大，表示其越接近真实分布；反之，就越接近生成分布。此外，  表示其Lipschitz常数为1。显然，Lipschitz连续在判别器上是难以约束的，为了更好地表达Lipschitz转化成权重剪枝，即要求参数w ∈ [−c, c]，其中为常数。因而判别器的目标函数为：

其中w ∈ [−c, c],生成器的损失函数为：

WGAN的贡献在于，从理论上阐述了因生成器梯度消失而导致训练不稳定的原因，并用Wasserstein距离替代了Jensen-Shannon散度，在理论上解决了梯度消失问题。此外，WGAN还从理论上给出了朴素GAN发生模式坍塌(mode collapse)的原因，并从实验角度说明了WGAN在这一点上的优越性。最后，针对生成分布与真实分布的距离和相关理论以及从Wasserstein距离推导而出的Lipschitz约束，也给了后来者更深层次的启发，如基于Lipschitz密度的 损失敏感GAN(loss sensitive GAN, LS-GAN)。

WGAN—GP

虽然WGAN在理论上解决了训练困难的问题，但它也有各种各样的缺点。在理论上，由于对函数（即判别器）存在Lipschitz-1约束，这个条件难以在神经网络模型中直接体现，所以作者使用了权重剪枝(clip) 来近似替代Lipschitz-1约束。显然在理论上，这两个条件并不等价，而且满足Lipschitz-1约束的情况多数不满足权重剪枝约束。而在实验上，很多人认为训练失败是由权重剪枝引起的，如图3。对此Ishaan Gulrajani提出了梯度带梯度惩罚的WGAN（WGAN with gradient penalty, WGAN-GP）[5]，将Lipschitz-1约束正则化，通过把约束写成目标函数的惩罚项，以近似Lipschitz-1约束条件。

因而，WGAN的目标函数可以写作

其中  是与之间的线性采样，即满足

此外，生成器的目标函数与WGAN相同，取第二项进行优化即可。

WGAN-GP的贡献在于，它用正则化的形式表达了对判别器的约束，也为后来GAN的正则化模型做了启示。此外WGAN-GP基本从理论和实验上解决了梯度消失的问题，并且具有强大的稳定性，几乎不需要调参，即在大多数网络框架下训练成功率极高。

 

LSGAN

虽然WGAN和WGAN-GP已经基本解决了训练失败的问题，但是无论是训练过程还是是收敛速度都要比常规 GAN 更慢。受WGAN理论的启发，Mao 等人提出了最小二乘GAN (least square GAN, LSGAN)[6]。LSGAN的一个出发点是提高图片质量。它的主要想法是为判别器D提供平滑且非饱和梯度的损失函数。这里的非饱和梯度针对的是朴素GAN的对数损失函数。显然，x越大，对数损失函数越平滑，即梯度越小，这就导致对判别为真实数据的生成数据几乎不会有任何提高。针对于此，LSGAN的判别器目标函数如下：

生成器的目标函数如下：

这里a, b, c满足b − c = 1和b − a = 2。根据[6]，它等价于f散度中的散度  ，也即是说，LSGAN用散度取代了朴素GAN的Jensen-Shannon散度。

最后，LSGAN的优越性在于，它缓解了GAN训练时的不稳定，提高了生成数据的质量和多样性，也为后面的泛化模型f-GAN提供了思路。

 

f-GAN

由于朴素GAN所代表的Jensen-Shannon散度和前文提到的LSGAN所代表的散度都属于散度的特例，那么自然而然地想到，其它f散度所代表的GAN是否能取得更好的效果。实际上，这些工作早已完成[7]，时间更是早过WGAN与LSGAN。甚至可以认为，是f-GAN开始了借由不同散度来代替Jensen-Shannon散度，从而启示了研究者借由不同的距离或散度来衡量真实分布与生成分布。首先衡量p(x), q(x)的f散度可以表示成如下形式：

其中下半连续映射