【统计学习课程】2 线性分类
总结自刘东老师《统计学习》课程,教材选用周志华老师《机器学习》西瓜书
每节都给了小结,可以快速了解每节内容
线性分类
- 分类问题
- 基本知识
- 分类 vs 回归
- 从回归到分类
- 小结
- Logistic回归
- 什么是Logistic回归
- 为什么用交叉熵作为优化目标
- 概率解释Logistic回归
- 推广的Logistic回归
- 小结
- 指数族分布和最大熵
- Logistic回归的解
- 没有闭式解
- Newton-Raphson法
- 梯度下降法
- Frank-Wolfe法
- 小结
- Logistic回归的概率解释——贝叶斯Logistic回归
- LDA
- 分类问题的几何解释
- LDA
- LDA和高斯Logistic回归
- 小结
- 感知机
- 感知机的优化目标与计算
- 感知机的对偶形式
- 小结
- 多分类与多标签
- 多分类
- 多标签
- 小结
- 总结
分类问题
基本知识
分类问题主要分为:二分类问题,多分类问题,多标签分类问题
二分类问题:每个数据只有一个标签,标签只有2种可能取值
多分类问题:每个数据只有一个标签,标签有多种可能取值
多标签问题:每个数据有多个标签,每个标签有多个可能取值
分类 vs 回归
回归问题:输出是连续的 vs 分类问题:输出是离散的
因此,
分类问题即经过量化的回归问题
所以分类问题其实比回归问题更复杂,难度更大
从回归到分类
线性回归的典型优化目标为
min w , b ∑ i = 0 N ( y i − ( w T x i + b ) ) 2 \min_{w,b}\sum_{i=0}^{N}(y_i-(w^Tx_i+b))^2 w,bmini=0∑N(yi−(wTxi+b))2
类似的,推广到二分类问题为,用回归的方法得到的结果就是
t = w T x + b t=w^Tx+b t=wTx+b
经过量化,结果变为
t = s i g n ( w T x + b ) t=sign(w^Tx+b) t=sign(wTx+b)
二分类问题的分类面为
w T x + b = 0 w^Tx+b=0 wTx+b=0
二分类的优化目标就变为
min w , b ∑ i = 0 N ( t i − s i g n ( w T x i + b ) ) 2 \min_{w,b}\sum_{i=0}^{N}(t_i-sign(w^Tx_i+b))^2 w,bmini=0∑N(ti−sign(wTxi+b))2
其中, t i t_i ti为每个样本的标签,对于二分类问题, t i ∈ { − 1 , + 1 } t_i\in\{-1,+1\} ti∈{−1,+1}
小结
1 分类是回归的量化,比回归更复杂
2 优化目标的改变与分类面的定义
Logistic回归
什么是Logistic回归
Logistic回归(对数似然回归),虽然叫回归,但实际是一个线性分类方法。
对于优化问题
min w , b ∑ i = 0 N ( t i − s i g n ( w T x i + b ) ) 2 \min_{w,b}\sum_{i=0}^{N}(t_i-sign(w^Tx_i+b))^2 w,bmini=0∑N(ti−sign(wTxi+b))2
Logistic回归的第一个修改:将符号函数sign改为sigmoid函数
s ( x ) = 1 1 + e − x s(x)=\frac{1}{1+e^{-x}} s(x)=1+e−x1
目的:符号函数在0点不可导(导数无穷大),而其他位置导数为0,是很难优化的;而sigmoid函数处处可导,同时sigmoid的输出在0到1之间,可以用于量化与分类
Logistic回归的第二个修改:将类别标签重映射
y i = t i + 1 2 y_i=\frac{t_i+1}{2} yi=2ti+1
目的:便于计算
Logistic回归的第三个修改:用交叉熵代替平方误差作为优化目标,待优化的函数为
min ∑ − y i log ( y i ^ ) − ( 1 − y i ) log ( 1 − y i ^ ) \min\sum-y_i\log(\hat{y_i})-(1-y_i)\log(1-\hat{y_i}) min∑−yilog(yi^)−(1−yi)log(1−yi^)
为什么用交叉熵作为优化目标
理解一
从概率的角度看,二分类问题可以被看作,估计一个输入属于类别+1的概率 P ( t i = + 1 ∣ x i ) P(t_i=+1|x_i) P(ti=+1∣xi)问题, P ( t i = + 1 ∣ x i ) > 0.5 P(t_i=+1|x_i)>0.5 P(ti=+1∣xi)>0.5就认为输入属于+1类。
对于一个输入 x i x_i xi,其通过sigmoid函数得到一个0~1的输出,这个输出值就可以看作它属于+1类的概率,即
P ( t i ∣ x , w , b ) = { y i ^ t i = + 1 1 − y i ^ t i = − 1 P(t_i|x,w,b)=\{\begin{matrix} \hat{y_i} \quad t_i=+1\\1-\hat{y_i}\quad t_i=-1\end{matrix} P(ti∣x,w,b)={yi^ti=+11−yi^ti=−1
由于标签经过了重映射,概率函数可以改写为
P ( t i ∣ x , w , b ) = ( y i ^ ) y i ( 1 − y i ^ ) 1 − y i P(t_i|x,w,b)=(\hat{y_i})^{y_i}(1-\hat{y_i})^{1-y_i} P(ti∣x,w,b)=(yi^)yi(1−yi^)1−yi
有了概率密度函数,那么即可用极大似然法对参数进行估计
max ∏ P ( t i ∣ x , w , b ) \max\prod P(t_i|x,w,b) max∏P(ti∣x,w,b)
也即
max ∑ log P ( t i ∣ x , w , b ) = max ∑ ( y i log ( y i ^ ) + ( 1 − y i ) log ( 1 − y i ^ ) ) \max\sum \log P(t_i|x,w,b)=\max\sum (y_i\log(\hat{y_i}) +(1-y_i)\log(1-\hat{y_i})) max∑logP(ti∣x,w,b)=max∑(yilog(yi^)+(1−yi)log(1−yi^))
两边添加负号,改写为最小化问题,即有优化最大熵的形式
理解二:
利用重映射的标签,真值的分布满足
P ( t i ∣ x , w , b ) = { y i t i = + 1 1 − y i t i = − 1 P(t_i|x,w,b)=\{\begin{matrix}{y_i} \quad t_i=+1\\1-{y_i}\quad t_i=-1\end{matrix} P(ti∣x,w,b)={yiti=+11−yiti=−1
y i = t i + 1 2 ∈ { 0 , 1 } y_i=\frac{t_i+1}{2}\in\{0,1\} yi=2ti+1∈{0,1}
估计的结果满足
Q ( t i ∣ x , w , b ) = { y i ^ t i = + 1 1 − y i ^ t i = − 1 Q(t_i|x,w,b)=\{\begin{matrix} \hat{y_i} \quad t_i=+1\\1-\hat{y_i}\quad t_i=-1\end{matrix} Q(ti∣x,w,b)={yi^ti=+11−yi^ti=−1
对于训练集,需要让估计的分布尽量与真值分布接近。
度量两个分布的距离,通常用K-L散度
D K − L ( P ∣ ∣ Q ) = C ( P , Q ) − H ( P ) D_{K-L}(P||Q)=C(P,Q)-H(P) DK−L(P∣∣Q)=C(P,Q)−H(P)
其中, C ( P , Q ) C(P,Q) C(P,Q)是交叉熵, H ( P ) H(P) H(P)是真值分布的熵
K-L散度越小,两个概率密度分布越接近。而其中,真值分布的熵不变且与优化参数无关,只有交叉熵与优化参数有关。因此,最小化K-L散度,即最小化交叉熵。
概率解释Logistic回归
假设已知类别的情况下,输入x的分布是高斯分布
p ( x ∣ t i = k ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) ) p(x|t_i=k)=\frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp{(-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k))} p(x∣ti=k)=(2π)D/2∣Σ∣1/21exp(−21(x−μk)TΣ−1(x−μk))
根据全概率公式
y i ^ = P ( t i = + 1 ∣ x i ) = p ( x i ∣ t i = + 1 ) P ( t i = + 1 ) p ( x i ∣ t i = + 1 ) P ( t i = + 1 ) + p ( x i ∣ t i = − 1 ) P ( t i = − 1 ) = 1 1 + e − ( w T x i + b ) \hat{y_i}=P(t_i=+1|x_i)=\frac{p(x_i|t_i=+1)P(t_i=+1)}{p(x_i|t_i=+1)P(t_i=+1)+p(x_i|t_i=-1)P(t_i=-1)}\\ =\frac{1}{1+e^{-(w^Tx_i+b)}} yi^=P(ti=+1∣xi)=p(xi∣ti=+1)P(ti=+1)+p(xi∣ti=−1)P(ti=−1)p(xi∣ti=+1)P(ti=+1)=1+e−(wTxi+b)1
可以用概率密度函数的参数,表示待估参数
推广的Logistic回归
Logistic回归也可以用基函数
将 w T x + b w^Tx+b wTx+b改用为 w T ϕ ( x ) w^T\phi(x) wTϕ(x),可以应对更复杂的情况时获得更高的分类准确率
小结
1 Logistic回归:用sigmoid函数代替符号函数;将标签-1、+1重映射到0和1;用交叉熵作为损失函数进行优化
2 交叉熵的理解:极大似然估计;概率密度的逼近
3 概率解释
4 推广:用基函数
指数族分布和最大熵
有如下形式的概率密度函数
p ( x ∣ ϑ ) = h ( x ) g ( ϑ ) exp ( ϑ T ϕ ( x ) ) p(x|\vartheta)=h(x)g(\vartheta)\exp(\vartheta^T\phi(x)) p(x∣ϑ)=h(x)g(ϑ)exp(ϑTϕ(x))
定义为指数族分布
伯努利分布,泊松分布,高斯分布等重要分布都可以写成指数族的形式
可以证明,指数族分布具有最大熵
Logistic回归的解
没有闭式解
考虑优化损失
min E ( w ) = ∑ − y i log ( y i ^ ) − ( 1 − y i ) log ( 1 − y i ^ ) \min E(w)=\sum-y_i\log(\hat{y_i})-(1-y_i)\log(1-\hat{y_i}) minE(w)=∑−yilog(yi^)−(1−yi)log(1−yi^)
直接求其关于参数的梯度为
∇ E ( w ) = ∑ i ( y i ^ − y i ) ϕ ( x i ) \nabla E(w)=\sum_i (\hat{y_i}-y_i)\phi(x_i) ∇E(w)=i∑(yi^−yi)ϕ(xi)
这一方程是非线性的( y i ^ \hat{y_i} yi^是sigmoid函数的结果),无法求得闭式解。但可以证明优化的损失函数是凸函数,即整个问题是凸优化问题,找到函数的局部最小值即求到了全局最小值。
凸优化的求解可以通过数值方法实现,基于二阶导的数值优化方法通常用Newton-Raphson法,基于一阶导的数值优化方法通常用梯度下降法和Frank-Wolfe法
Newton-Raphson法
基于二阶导的方法利用了函数极值点一阶导为0的性质,对参数直接进行更新。
函数 f ( x ) f(x) f(x)的Taylor展开到二阶为
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 0.5 f ′ ′ ( x 0 ) ( x − x 0 ) 2 f(x)=f(x_0)+f'(x_0)(x-x_0)+0.5f''(x_0)(x-x_0)^2 f(x)=f(x0)+f′(x0)(x−x0)+0.5f′′(x0)(x−x0)2
对于局部极值点,满足
f ′ ( x ∗ ) = 0 → x ∗ = x 0 − f ′ ( x 0 ) f ′ ′ ( x 0 ) f'(x^*)=0\to x^*=x_0-\frac{f'(x_0)}{f''(x_0)} f′(x∗)=0→x∗=x0−f′′(x0)f′(x0)
对于Logistic回归优化的损失函数,二阶导
H = ∇ ∇ E ( w ) = ∑ i y i ^ ( 1 − y i ^ ) ϕ ( x i ) ϕ T ( x i ) = Φ T R Φ H=\nabla\nabla E(w)=\sum_i \hat{y_i}(1-\hat{y_i})\phi(x_i)\phi^T(x_i)=\Phi^TR\Phi H=∇∇E(w)=i∑yi^(1−yi^)ϕ(xi)ϕT(xi)=ΦTRΦ
则系数更新方程为
w ( n e w ) = w ( o l d ) − ( Φ T R Φ ) − 1 Φ T ( y ^ − y ) w^{(new)}=w^{(old)}-(\Phi^TR\Phi)^{-1}\Phi^T(\hat{y}-y) w(new)=w(old)−(ΦTRΦ)−1ΦT(y^−y)
特点:基于二阶导的方法,损失函数下降很快,但接近极小值的时候振荡很明显(方差大),一次运算不一定能收敛到最优解
梯度下降法
梯度下降法相比Newton-Raphson法更直接,因为任意函数在足够小的区间内都可以看作是局部线性的,那么一个点的一阶导就是这个区间内的斜率,沿着斜率方向向极小值点走一小步,就可以保证每迭代一次函数值都减小一点。
函数 f ( x ) f(x) f(x)的Taylor展开到一阶为
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 0.5 f ′ ′ ( x 0 ) ( x − x 0 ) 2 f(x)=f(x_0)+f'(x_0)(x-x_0)+0.5f''(x_0)(x-x_0)^2 f(x)=f(x0)+f′(x0)(x−x0)+0.5f′′(x0)(x−x0)2
为了找到局部极小值,就要保证
f ( x ( n e w ) ) < f ( x ( o l d ) ) f(x^{(new)})
则 x x x的更新就是
x ( n e w ) = x ( o l d ) − η f ′ ( x ( o l d ) ) x^{(new)}=x^{(old)}-\eta f'(x^{(old)}) x(new)=x(old)−ηf′(x(old))
其中, η \eta η是一个很小的正数,被称为学习率
对于求解的参数是向量的情况,只需要将上式的导数推广为梯度即可。
特点:一阶导的方法更易收敛到最优解,因为选取合适的学习率就可以保证每一步迭代都在减小损失函数。但是,学习率是一个超参,需要人为确定,如果过大会导致在极小值附近振荡;如果过小收敛又会很慢。一般常用的做法是取 1 / ( n + 1 ) 1/(n+1) 1/(n+1), n n n是迭代步数,这样可以保证前期的收敛速度,并且逐渐减小步长以保证收敛。
Frank-Wolfe法
Frank-Wolfe法针对的问题是有约束的优化问题
min f ( x ) , s u b j e c t t o x ∈ X \min{f(x)}, subject\; to\; x\in {\Bbb X} minf(x),subjecttox∈X
对于以一个点 x 0 x_0 x0的导数 f ′ ( x 0 ) f'(x_0) f′(x0)为斜率的线性函数,在约束范围内有最小值
s = min x f ′ ( x 0 ) , s u b j e c t t o x ∈ X s=\min{xf'(x_0)},subject \; to \; x\in {\Bbb X} s=minxf′(x0),subjecttox∈X
则从 x 0 x_0 x0到 s s s沿着线找到函数取极小值的点 x 1 x_1 x1
x 1 = γ s + ( 1 − γ ) x 0 , 0 < γ < 1 x_1=\gamma s +(1-\gamma)x_0, 0<\gamma<1 x1=γs+(1−γ)x0,0<γ<1
Frank-Wolfe法可以理解为,在凸函数上任意取约束范围内一个点,过这个点有一个切面,根据局部线性的性质可以确定,原本的凸函数的极小值一定要沿着切面下降的方向找。
特点:Frank-Wolfe法是针对有约束问题的,因此显得不那么通用,而有约束问题又可以转换为无约束问题和正则化,所以Frank-Wolfe法就不那么常用了。
小结
1 Logistic回归没有闭式解(解析解),但损失函数是凸函数,可以数值优化求解
2 Newton-Raphson法:基于二阶导,损失函数下降快,但容易振荡
3 梯度下降法:基于一阶导,需要合适的学习率保证收敛足够快且不容易振荡
4 Frank-Wolfe法:只适用于有约束问题
Logistic回归的概率解释——贝叶斯Logistic回归
和所有的贝叶斯方法类似,都需要确定系数的先验概率,设为
p ( w ) = N ( w ∣ m 0 , S 0 ) p(w)=N(w|m_0,S_0) p(w)=N(w∣m0,S0)
又因为样本的概率函数为
P ( t i ∣ x , w , b ) = ( y i ^ ) y i ( 1 − y i ^ ) 1 − y i P(t_i|x,w,b)=(\hat{y_i})^{y_i}(1-\hat{y_i})^{1-y_i} P(ti∣x,w,b)=(yi^)yi(1−yi^)1−yi
那么对数后验概率就有
ln p ( w ∣ x i , t i ) = ∑ i − y i ln y i ^ − ( 1 − y i ) ln ( 1 − y i ^ ) + 1 2 ( w − m 0 ) T S 0 − 1 ( w − m 0 ) + c o n s t \ln{p(w|x_i,t_i)}=\sum_{i}{-y_i\ln \hat{y_i} -(1-y_i)\ln (1-\hat{y_i})+\frac{1}{2}(w-m_0)^TS_0^{-1}(w-m_0) +const} lnp(w∣xi,ti)=i∑−yilnyi^−(1−yi)ln(1−yi^)+21(w−m0)TS0−1(w−m0)+const
对上式优化时,寻找令概率函数取最大值的 w w w即可
LDA
分类问题的几何解释
Logistic回归中,我们预测的结果是
y ^ = s i g m o i d ( w T x + b ) \hat{y}=sigmoid(w^Tx+b) y^=sigmoid(wTx+b)
w T x w^Tx wTx可以看作是两个向量的点乘,即 x x x向 w w w的投影,再设定一个阈值进行分类。
线性判别式分析(Linear Discriminant Analysis, LDA)基于的就是这个思想,直接找出合适的投影方法确定分类面。
最合适的投影方向,就是投影后能保证不同类间区分度最大的方向,但如何数学描述?
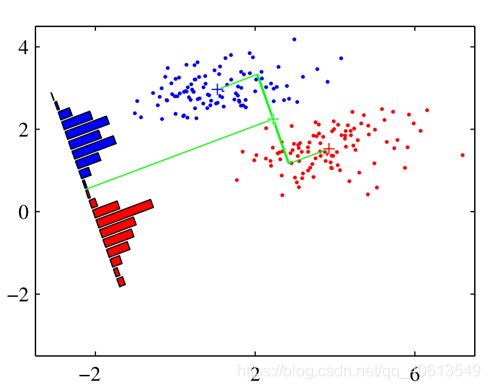
LDA
Fisher给出的最大类间区分与最小类内方差的公式
J ( w ) = ( ( m + 1 − m − 1 ) ) 2 S + 1 + S − 1 J(w)=\frac{((m_{+1}-m_{-1}))^2}{S_{+1}+S_{-1}} J(w)=S+1+S−1((m+1−m−1))2
其中, m m m是一个类内 w T x w^Tx wTx的均值, S S S是对应的方差
由此可以得到 w w w的解为
w ∝ S − 1 ( v + 1 − v − 1 ) S = v a r i a n c e { x ∣ t i = + 1 } + v a r i a n c e { x ∣ t i = − 1 } v ± 1 = m e a n { x ∣ t i = ± 1 } w\propto S^{-1}(v_{+1}-v_{-1})\\S=variance\{ x|t_i=+1\}+variance\{ x|t_i=-1\}\\v_{\pm1}=mean\{x|t_i=\pm1\} w∝S−1(v+1−v−1)S=variance{x∣ti=+1}+variance{x∣ti=−1}v±1=mean{x∣ti=±1}
得到的分类面的方程为
w T x = b , b = m + 1 − m − 1 2 w^Tx=b,b=\frac{m_{+1}-m_{-1}}{2} wTx=b,b=2m+1−m−1
LDA和高斯Logistic回归
如果每个类别 t i t_i ti中的变量 x x x满足高斯概率密度函数
p ( x ∣ t i = k ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ k ) T Σ − 1 ( x − μ k ) ) p(x|t_i=k)=\frac {1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp{(-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k))} p(x∣ti=k)=(2π)D/2∣Σ∣1/21exp(−21(x−μk)TΣ−1(x−μk))
那么其对数形式为
l o g o d d s = Σ − 1 ( μ + 1 − μ − 1 ) x i + b log\;odds=\Sigma^{-1}(\mu_{+1}-\mu_{-1})x_i+b logodds=Σ−1(μ+1−μ−1)xi+b
而LDA的系数满足
w ∝ S − 1 ( v + 1 − v − 1 ) w\propto S^{-1}(v_{+1}-v_{-1}) w∝S−1(v+1−v−1)
也就是说类内变量满足高斯分布时,Logistic回归和LDA等价
小结
1 LDA思想:最大化类间差异,最小化类内方差
2 w ∝ S − 1 ( v + 1 − v − 1 ) w\propto S^{-1}(v_{+1}-v_{-1}) w∝S−1(v+1−v−1)
3 LDA和高斯Logistic回归等价
感知机
感知机的优化目标与计算
起初分类问题的优化目标都是
min w , b ∑ i = 0 N ( t i − s i g n ( w T x i + b ) ) 2 \min_{w,b}\sum_{i=0}^{N}(t_i-sign(w^Tx_i+b))^2 w,bmini=0∑N(ti−sign(wTxi+b))2
也就是从回归推广而来的损失函数。由于其不可导,引出了Logistic回归,但求解依然困难,只能进行数值优化。
Rosenblatt提出将优化目标修改为
min w ∑ t i ≠ s i g n ( w T x i ) − t i w T x i \min_{w}\sum_{t_i\neq sign(w^Tx_i)}{-t_iw^Tx_i} wminti=sign(wTxi)∑−tiwTxi
即,将所有误分类的估计结果的绝对值累加,优化使其最小。显然,最小化要保证①误分类的点尽可能少,②误分类的点尽可能靠近分类面(也就是只希望一些比较难的点分类错误)
那么,利用传统的梯度下降方法,可以优化系数
w ( n e w ) = w ( o l d ) − η ∑ m i s − p o i n t s t i x i w^{(new)}=w^{(old)}-\eta \sum_{mis-points} {t_ix_i} w(new)=w(old)−ηmis−points∑tixi
如果用随机学习(stochastic learning)的方法优化则是
w ( n e w ) = w ( o l d ) − η t i x i , i f t i w ( o l d ) ⋅ x i < 0 w^{(new)}=w^{(old)}-\eta {t_ix_i},if\;t_iw^{(old)} \cdot x_i<0 w(new)=w(old)−ηtixi,iftiw(old)⋅xi<0
梯度下降方法也可以动态的看作:
(1)随机初始化系数后,得到初始的分类面,所有误分类的点都会产生对分类面的拉力;
(2)误分类点拉力的合力会扯动分类面,得到新的分类面;
(3)新的分类面再进行分类,得到新的误分类点与对应的拉力;
(4)反复扯动分类面,直至没有误分类点,或误分类点合力为0(收敛)
而随机学习/增量学习,就是每有一个误分类样本点就扯动一下分类面。
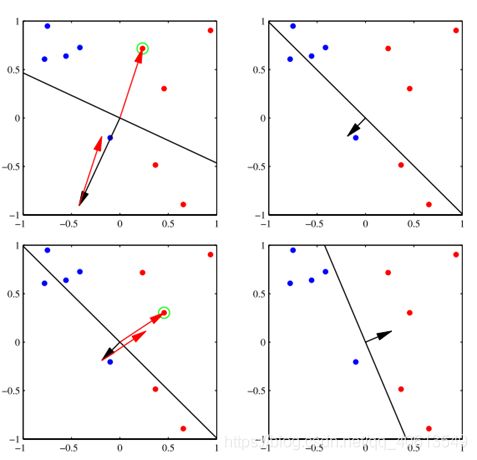
感知机的对偶形式
如果我们初始化系数为0,那么用梯度下降迭代后得到的系数结果就是
w = ∑ α i t i x i w=\sum{\alpha_it_ix_i} w=∑αitixi
即所有样本点都有对应的系数 α i \alpha_i αi
对于每个误分类的点,更新其自身的系数,直至收敛。那么,对一个新的点,分类结果就是
t ^ = s i g n ( ∑ α i t i x i ⋅ x ) \hat t=sign(\sum{\alpha_it_ix_i} \cdot x) t^=sign(∑αitixi⋅x)
小结
1 感知机:改变了优化目标,尽可能减少误分类点的个数和误分类点与分类面的距离
2 误分类点扯动分类面,逐渐优化系数
3 对偶形式:每个样本点优化各自的系数
多分类与多标签
多分类
将二分类推广到多分类有两种方法:
(1)1类 vs 其他类
(2)1类 vs 1类
两者都存在局限性

左图用1类 vs 其他类,绿色区域则既是1类又是2类;右图用1类 vs 1类,绿色区域则不属于任何一类。
之前在Logistic回归二分类问题中,我们用全概率公式可以计算一个样本属于+1类的概率
y i ^ = P ( t i = + 1 ∣ x i ) = p ( x i ∣ t i = + 1 ) P ( t i = + 1 ) p ( x i ∣ t i = + 1 ) P ( t i = + 1 ) + p ( x i ∣ t i = − 1 ) P ( t i = − 1 ) = 1 1 + e − ( w T x i + b ) \hat{y_i}=P(t_i=+1|x_i)=\frac{p(x_i|t_i=+1)P(t_i=+1)}{p(x_i|t_i=+1)P(t_i=+1)+p(x_i|t_i=-1)P(t_i=-1)}\\ =\frac{1}{1+e^{-(w^Tx_i+b)}} yi^=P(ti=+1∣xi)=p(xi∣ti=+1)P(ti=+1)+p(xi∣ti=−1)P(ti=−1)p(xi∣ti=+1)P(ti=+1)=1+e−(wTxi+b)1
那么把这个式子推广到多类别就有
y i ^ = P ( t i = k ∣ x i ) = p ( x i ∣ t i = k ) P ( t i = k ) ∑ j p ( x i ∣ t i = j ) P ( t i = j ) \hat{y_i}=P(t_i=k|x_i)=\frac{p(x_i|t_i=k)P(t_i=k)}{\sum _{j}{p(x_i|t_i=j)P(t_i=j)}} yi^=P(ti=k∣xi)=∑jp(xi∣ti=j)P(ti=j)p(xi∣ti=k)P(ti=k)
这样就不再会出现刚才的一个样本分到多个类或者不属于任一类的情况,这也就是softmax激活的基础(softmax需要满足 ln p ( x i ∣ t i = k ) P ( t i = k ) = w k T x i + b k \ln p(x_i|t_i=k)P(t_i=k)=w_k^Tx_i+b_k lnp(xi∣ti=k)P(ti=k)=wkTxi+bk)
多标签
一个样本如果可以有多个标签,则称为多标签问题,比如一首歌的分类。
将二分类应用于多标签问题时,由于标签通常不是互斥的,所以一个样本要对每个可能的标签进行判断,属于/不属于。如果最终只需要一个标签,则挑出属于概率最高的标签。
小结
二分类方法不能直接用于多分类/多标签问题,需要合适的推广。
总结
1 分类vs回归:分类存在量化,分类更难解决
2 Logistic回归:估计样本属于+1类的概率,没有闭式解但可以数值求解(3种常见数值解方式)
3 LDA:最大化类间区分,最小化类内方差
4 感知机:修改损失函数,利用误分类点调整分类面
5 多分类与多标签的推广