【百科】逻辑代数
http://baike.baidu.com/view/812755.htm?fr=ala0_1
逻辑代数是分析和设计逻辑电路的数学基础。逻辑代数是由英国科学家乔治·布尔(George·Boole)创立的，故又称布尔代数。
编辑本段
简介
逻辑代数是分析和设计逻辑电路的数学基础。逻辑代数是由英国科学家乔治·布尔(George·Boole)创立的，故又称 布尔代数。
布尔
编辑本段
逻辑代数中的几个概念 参与逻辑运算的变量叫逻辑变量，用字母A，B……表示。每个变量的取值非0 即1。 0、1不表示数的大小，而是代表两种不同的逻辑状态。
逻辑代数
编辑本段
逻辑代数的基本规则
代入规则
任何一个含有变量 X 的等式，如果将所有出现 X 的位置，都代之以一个逻辑函数 F，此等式仍然成立。对偶规则
设 F 是一个逻辑函数式，如果将 F 中的所有的 * 变成 +，+ 变成 *，0 变成 1，1 变成 0，而变量保持不变。那么就的得到了一个逻辑函数式 F'，这个 F' 就称为 F 的对偶式。如果两个逻辑函数 F 和 G 相等，则它们各自的对偶式 F' 和 G' 也相等。
逻辑代数
反演规则
当已知一个逻辑函数 F，要求 ¬F 时，只要把 F 中的所有 * 变成 +，+ 变成 *，0 变成 1，1 变成 0，原变量变成反变量，反变量变成原变量，即得 ¬F。
编辑本段
逻辑函数的标准形式 逻辑变量的逻辑与运算叫做与项，与项的逻辑或运算构成了逻辑函数的与或式，也叫做积之和式(SP form)。 逻辑变量的逻辑或运算叫做或项，或项的逻辑与运算构成了逻辑函数的或与式，也叫做和之积式(PS form)。
逻辑代数
最小项
对于 n 个变量的逻辑函数而言，它的与项如果包含 n 个文字，即每个变量以原变量或反变量的形式出现一次且只出现一次，那么这个与项就称为该逻辑函数的最小项。最大项
对于 n 个变量的逻辑函数而言，它的或项如果包含 n 个文字，即每个变量以原变量或反变量的形式出现一次且只出现一次，那么这个或项就称为该逻辑函数的最大项。
编辑本段
逻辑函数的化简 运用逻辑代数的基本公式及规则可以对逻辑函数进行变换，从而得到表达式的最简形式。这里所谓的最简形式是指最简与或式或者是最简或与式，它们的判别标准有两条：(1)项数最少；(2)在项数最少的条件下，项内的文字最少。
逻辑代数
编辑本段
其他
逻辑代数是按一定的逻辑关系进行运算的代数，是分析和设计 数字电路的数学工具。在逻辑代数，只有０和１两种逻辑值， 有与、或、非三种基本 逻辑运算，还有与或、与非、与或非、异或几种导出逻辑运算。
逻辑是指事物的因果关系，或者说条件和结果的关系，这些因果关系可以用逻辑运算来表示，也就是用逻辑代数来描述。事物往往存在两种对立的状态，在逻辑代数中可以抽象地表示为 0 和 1 ，称为逻辑0状态和逻辑1状态。 逻辑代数中的变量称为
逻辑变量，用大写字母表示。逻辑变量的取值只有两种，即逻辑0和逻辑1，0 和 1 称为逻辑常量，并不表示数量的大小，而是表示两种对立的逻辑状态。 逻辑代数是分析和设计逻辑电路的数学基础。逻辑代数是由英国科学家乔治·布尔(George·Boole)创立的，故又称布尔代数。 当逻辑代数的逻辑状态多于2种时（如0、1、2或更多状态时），其通用模型的基本逻辑有2个。 一个是从一种状态变为另一种状态的逻辑，是一个一元逻辑； 另外一种是两种状态中按照某种规则（比如比较大小）有倾向性的选择出其中一种状态的逻辑，这是一个二元逻辑。 依据这两种逻辑，可以表达任意多状态的任意逻辑关系，即最小表达式。 即任意多状态的逻辑是完备的。 当逻辑状态数扩展有理数量级甚至更多。任意数学运算都可以用两个运算关系来联合表达：加减法和比较大小。 逻辑代数，亦称布尔代数，是英国数学家乔治 布尔（George Boole）于1849年创立的。在当时，这种代数纯粹是一种数学游戏，自然没有物理意义，也没有现实意义。在其诞生100多年后才发现其应用和价值。 其规定： 1．所有可能出现的数只有0和1两个。 2．基本运算只有“与”、“或”、“非”三种。 与运算（逻辑与、逻辑乘）定义为： 0·0＝0 0·1＝0 1·0＝0 1·1＝1 或运算（逻辑或、逻辑加）定义为： 0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝1 至此布尔代数宣告诞生。 二、基本公式 如果用字母来代替数（字母的取值非0即1），根据布尔定义的三种基本运算，我们马上可推出下列基本公式： A·A＝A A＋A=A A·0＝0 A＋0=A A·1＝A A＋1=1 上述公式的证明可用穷举法。如果对字母变量所有可能的取值，等式两边始终相等，该公式即告成立。
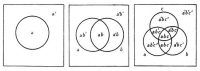
类代数 类代数是类逻辑的代数化。所谓类逻辑是从外延上理解的一阶一元谓词的逻辑。一元谓词的外延指称该谓词所适用的个体的类。由论域中所有个体组成的类叫全类，记作 1。不含有任何事物的类叫空类，记作0。考虑全类的所有子类，即包含于其中的类（包括1和0），令ａ,ｂ,с,…为这样的类变元。由论域中不属于ａ类的个体组成的类叫做ａ的补，记作ａ'。由或属于ａ类或属于ｂ类的个体组成的类叫做ａ与ｂ的逻辑和（并类）,记作ａ∪ｂ。由既属于 a类又属于 b类的个体组成的类叫做ａ与ｂ的逻辑积（交类），记作ａ∩ｂ，简记作ａｂ。如果ａ类与ｂ类所含的个体相同,则称ａ与ｂ等同,记作ａ=ｂ。ａ与ｂ不等同记作ａ≠ｂ。1和0是两个特定的类常元。',∪和∩是三种逻辑运算，分别叫类的取补、求和（加法）和求积（乘法）。此外，还可以通过定义引入包含于关系吇，例如把ａ吇ｂ定义为ａ∩ｂ' =0。于是自然有:对于任何类ａ,0吇ａ吇1。 在类代数中，不带有主词存在断定的直言命题ａAｂ、ａEｂ、ａIｂ和ａOｂ，可表示为ａ∩ｂ'=0、ａ∩ｂ=0、ａ∩ｂ≠0和ａ∩ｂ' ≠0。传统逻辑中三段论第1格 AAA式可表示为： 如果с∩ｂ' =0且ａ∩с' =0，则ａ∩ｂ' =0。第3格EIO式可表示为： 如果с∩ｂ=0且с∩ａ≠0，则ａ∩ｂ' ≠0。类代数的运算满足下表中列出的基本定律。 类代数的基本定律 幂等律 ａ∪ａ=ａ ａ∩ａ=ａ 交换律 ａ∪ｂ=ｂ∪ａ ａ∩ｂ=ｂ∩ａ 结合律 ａ∪(ｂ∪с)=(ａ∪ｂ)∪с ａ∩(ｂ∩с)=(ａ∩ｂ)∩с 吸收律 ａ∪(ａ∩ｂ)=ａ ａ∩(ａ∪ｂ)=ａ 分配律 ａ∪(ｂ∩с)=(ａ∪ｂ)∩(ａ∪с) ａ∩(ｂ∪с)=(ａ∩ｂ)∪(ａ∩с) 幺元律 0∪ａ =ａ 0∩ａ =ａ 1∪ａ =1 0∩ａ =0 补余律 ａ∪ａ' =1 ａ∩ａ' =0 从这些定律出发，特别是只需以其中的交换律、分配律、前两个幺元律和补余律作为初始定律即公理，就可以推导出类逻辑的所有定律（定理）。类逻辑的内容比传统的三段论理论要丰富得多，大致相当于只包含一元谓词的一阶谓词逻辑（见谓词逻辑）。一般的谓词逻辑也可以用更进一步的代数方法处理，但已超出通常所谓的逻辑代数的范围。
命题代数 命题代数在结构上与类代数完全相同。只要对类代数中的符号另作命题逻辑的解释，或者干脆改为相应的命题逻辑符号，就得到命题代数。即把类变元改为命题变元p,q,ｒ,…；改为否定词塡（“并非”）；∪改为析取词∨（“或者”）；∩改为合取词∨（“并且”）。1和0分别解释为特定的逻辑上真的命题和逻辑上假的命题,或称有效命题和矛盾命题;＝表示两命题逻辑上等值。这时，塡、∨和∧作为命题运算正好满足形式上与类代数的基本定律相对应的定律，而整个命题代数可包括命题逻辑的全部内容。命题代数和类代数可以有各种形式的公理系统，尤其是都可以有关于布尔展开式的定理，它相当于命题逻辑中的优析取范式和优合取范式的定理。 逻辑代数与命题代数有所不同。它还可以把1和0分别解释为命题的真和假,令变元只取1和0为值,即令其为二值的真值变元,并把塡、∨和∧解释为真值运算,从而得到一种提供命题真值运算定律的真值代数。而且，在二值的真值代数中特别可以有定理“p=1或p=0”，但在一般的命题代数和类代数中却没有与此相应的定理。