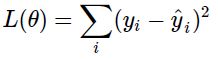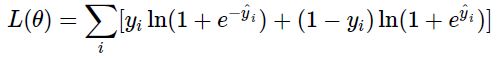算法(XGBoost)
目录
- 一、Get Started with XGBoost
- 二、XGBoost算法介绍
- 2.1 Objective Function:
- 2.1.1 Training Loss Function
- 2.1.2 Regularization Term
- 2.2 Decision tree ensemble model
- 2.3 Tree Boosting
- 2.4 Model Complexity(优化正则化项)
- 2.5 The Structure Score
- 2.6 Learn the tree structure
- 三、XGBoost算法应用
一、Get Started with XGBoost
https://xgboost.readthedocs.io/en/latest/get_started.html
import xgboost as xgb
# read in data
dtrain = xgb.DMatrix('demo/data/agaricus.txt.train')
dtest = xgb.DMatrix('demo/data/agaricus.txt.test')
# specify parameters via map
param = {'max_depth':2, 'eta':1, 'objective':'binary:logistic' }
num_round = 2
bst = xgb.train(param, dtrain, num_round)
# make prediction
preds = bst.predict(dtest)二、XGBoost算法介绍
XGBoost stands for “Extreme Gradient Boosting”
2.1 Objective Function:
Objective Function = Training Loss + Regularization (目标函数 = 损失 + 正则)
目标函数的作用:机器学习的终极目标是训练模型,通过寻找最优的参数θ,θ可以最好地fit数据X和y。为了找寻这最好的模型,就要定义目标函数来衡量how well the model fit the training data
目标函数包含了两部分:Training Loss 和 regularization term
![]()
2.1.1 Training Loss Function
损失函数:衡量模型对training data的预测能力
常用的L(θ) 有:
2.1.2 Regularization Term
正则化项控制模型的复杂度,可以帮助避免overfitting(我们想要的是一个既简单又预测能力强的模型)
2.2 Decision tree ensemble model
1.单个CART树
集成树模型有一系列的CART树组成。 (Classification and Regression Tree)
每个生成的CART树会给树的每个叶子节点打分:
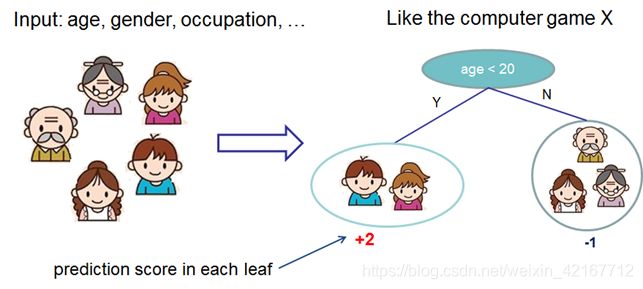
例如:预测一个人是否喜欢玩游戏,数据样本的属性有年龄、性别、职业、是否经常使用电脑。。。
一个最简单的CART树以age为分类节点,分成两个叶子节点,并给相应的叶子打上分数
2.集成所有生成的CART树
集成方法:要预测一个样本时,将所有CART树的预测分数加起来
例如:要预测一个小男孩是否喜欢打游戏:小男孩样本的属性为年龄<20,每日使用电脑
那么将所有包含小男孩样本的叶子结点得分数相加,就是对小男孩样本的预测值
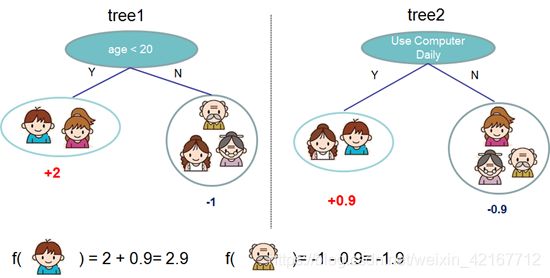
可以发现这两棵树互相补足,用数学公式表示如下:
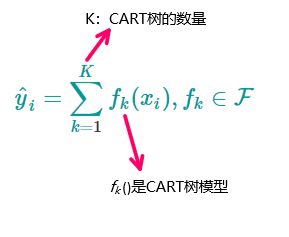
一个样本x的预测 = K个CART决策树对样本x的预测值之和
2.3 Tree Boosting
1.如何构造CART树
首先,我们想知道:what are the parameters of trees? 机器学习中所要“学习”到的东西就是 fk
fk :就是一个一个的CART树模型,包含了树的结构和叶子节点上的分数(structure
of the tree and the leaf scores)
然而learning tree structure 比传统的优化问题更难 ( traditional optimization problem where you can simply take the gradient)难在:很难一次性学完所有的CART树。
所以使用additive strategy: 改进我们所学到的,并一次添加一棵树(fix what we have learned, and add one new tree at a time)每轮迭代添加1棵树,此轮所有树的预测结果合并要比上次更好
2.Additive strategy数学模型
将additive strategy思想写成数学模型:

3.which tree do we want at each step?
每轮迭代中,什么样的树是我们想要的?当然是可以优化目标函数(objective function)的那种树

3.1 用MSE(Mean squared error )作为损失函数套进上面的式子
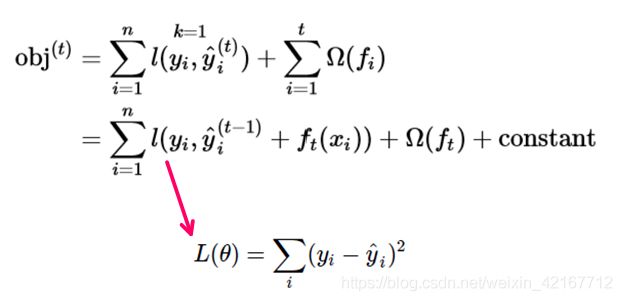 会得到objective function 变为:
会得到objective function 变为:

要优化目标函数,转而变为减少残差
用MSE作为损失函数是友好的,因为会化简成 一个 带有一次项和二次项的方程,再加上正则化项和一些常数
然而对于其他的loss function就不能得到如此漂亮的形式了,所以就要有一个一般形式公式,来构造一次项,二次项。
3.2 泰勒展开式得到目标函数的一般形式

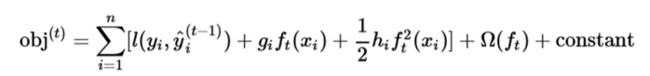
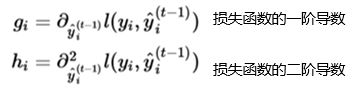
又因为,第t轮的目标函数是由上一轮的预测+这一轮的预测综合起来而得到的
那么前一轮得到的模型,对于第t棵树来说是固定值,所以可以将之前的模型当作常数值,移到constant常数项中,然后删去
得到第t轮的目标函数如下:
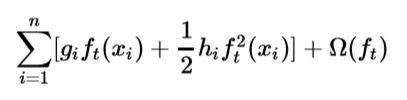
这个方程就变成了新CART树的优化目标,这样定义新的化简后的目标方程的好处是,这个目标函数的值只由两个变量决定,g和h(一阶导数,二阶导数),这样有利于更换损失方程loss function
2.4 Model Complexity(优化正则化项)
以上介绍了如何训练的步骤,优化损失函数。接下来要介绍如何优化正则化项
我们首先要定义树的复杂程度 the complexity of the tree: Ω(f)
1.重新定义tree f(x) :CART树的结构,叶子结点上的打分
新定义的f(x) :
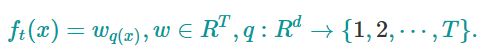
w : vector of scores on leaves(叶子节点上的分数所组成的向量)
q : is a function assigning each data point to the corresponding leaf (方程:将各个样本分配到相应的叶子节点上)
T : is the number of leaves
2.重新定义完f(x), 在XGBoost中,将如下方程定义为模型复杂度方程(也就是正则化项)
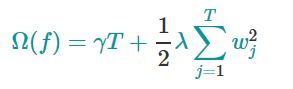
γ 是 惩 罚 系 数 γ是惩罚系数 γ是惩罚系数
当然不止一种方式定义模型的复杂度(complexity),但这一种在实际中表现不错,
(正则化项通常在普通的树模型包中没有被认真对待,因为tree learning通常强调的是改善不纯度,往往忽视了模型复杂度的控制,通过正式定义复杂度公式,我们能更好的了解和获得泛化性能好的模型)
2.5 The Structure Score
结合之前得到的经过泰勒展开的目标函数 和 复杂度方程,
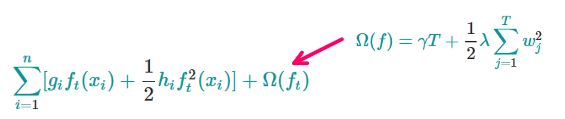
我们得到第 t 棵树的目标方程如下
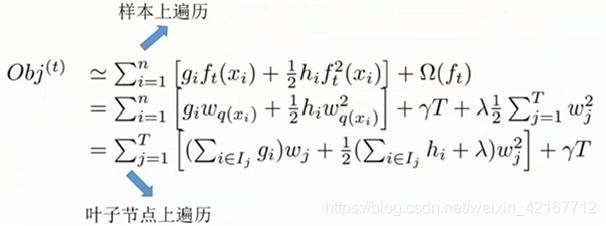
j指的是是第 j 个叶子节点![]()
再进一步,压缩表达式:
![]()
得到如下目标函数

求导,得到最优的wj ,能使得总体目标函数(综合了损失函数和正则化项)最优
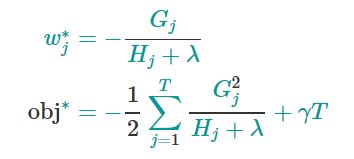
总结:本节介绍了如何计算CART树结构的分数(如何评估一个树的好坏)
The equation measures how good a tree structure q ( x ) q(x) q(x) is
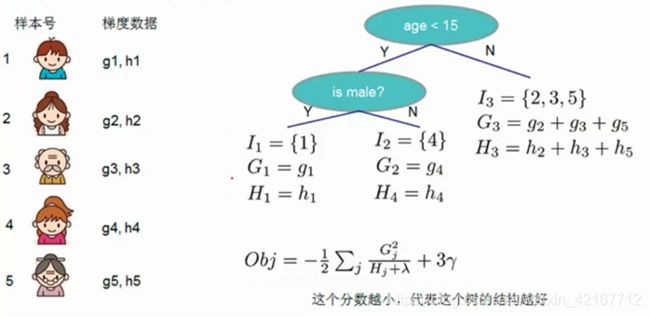
2.6 Learn the tree structure
现在我们有了如何衡量一个树的好坏的目标方程。理想的做法是,枚举所有可能的CART树并找到最好的,这实际上是很难的,所以我们试着一次迭代就改进树一点
我们试着将一个叶子节点分裂成两个,分裂节点所得到的score如下
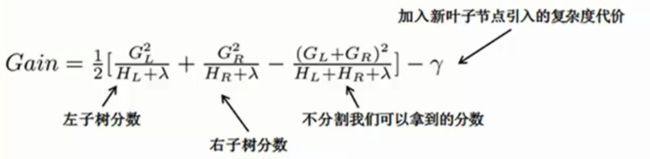
如果分裂后的Gain小于小于 γ γ γ(复杂度代价)我们就不会去添加分支
为了search optimal split,为了有效率的寻找,我们将样本按照顺序排列,然后计算所有的possible split solution
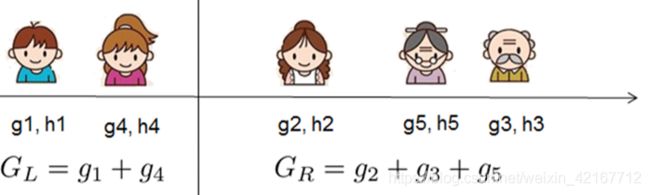
总结:本节主要介绍如何根据Gain来决定是否分裂,分裂后的左子树score,右子树score