2.4评价指标
2.4.1AUC
ROC曲线下的面积。信号探测理论中,ROC曲线用来评价某种分类器的分类效果。这种评价指标可以用来衡量链路预测算法的精确度
事实上,AUC可以理解为在测试集中随机选择一条边的分数值比随机选择一条不存在的边的分数值大的概率
独立比较n次,大于+1(设有n'次),等于+0.5(设有n''次),小于不加,AUC定义为(n'+0.5n'')/n
如果所有分数都是随机产生,AUC≈0.5,所以AUC大于0.5的程度衡量了算法在多大程度上比随机选择的方法精确
2.4.2精确度Precision
只关心前面几条边预测是否准确
假设m个预测准确,排在前L的边中有m个在测试集中,精确度定义为m/L,对于给定的L,精确度越大预测越准确
比如两个算法AUC一致,而某个的Precision大于另外的,就说明这个算法更好
2.4.3排序分
考虑了测试集中的边在最终排序中的位置
排序分值越小算法预测效果越好
三、基于相似性的链路预测
最简单的一种框架
3.1基于局部信息的相似
3.1.1 基于共同邻居的相似性指标
1.CN指标:又称结构等价,相似性定义为共同邻居数,等于两节点之间长度为二的路径数目,注意前7种指标(1+6):
2.AA指标,思想是度小得共同邻居节点的贡献度大于度大的共同邻居节点,上图第9
3.RA(resource allocation)指标【周涛】,上图第10。当网络的平均度较小时 RA 和 AA 差别不大,但是当平均度较大时,就有很大的区别了。
3.1.2 偏好相似连接性
应用优先连接的方法可以产生无标度网络,在该网络中,一条即将加入的新边连接到节点 x 的概率正比于节点 x 的度k(x) ,因此新边连接节点 x 和 y 的概率正比于两节点度的乘积。该算法的复杂度较其他算法低,因为需要的信息量最少,上图优先连接指标(PA)
3.1.3 局部朴素贝叶斯模型
引入一个角色函数,用于揭示不同共同邻居的不同作用。在食物链网络、蛋白质相互作用网络、科学家合作网络等具有优点
3.2基于路径的相似性指标
3.2.1 局部路径指标
局部路径指标 (local path) , LP 是在共同邻居指标的基础上考虑三阶邻居的贡献,
其中 α 为可调节参数,用于控制三阶路径的作用,当 α = 0时, LP 指标就等于 CN扩展到n阶:
3.2.2 Katz 指标
考虑的是所有的路径数,且对于短路径赋予较大的权重,而长路径赋予较小的权重
3.2.3 LHN-II指标
基本思想时一般等价,与结构等价不同,定义如果两个节点所连接的节点之间相似,那么这两个节点也相似,即使没有共同邻居节点。
3.3基于随机游走的相似性指标
3.3.1 全局随机游走
有一类相似性算法是基于随机游走定义的,包括平均通勤时间、Cos+指标 、有重启的随机游走 、SimRank指标,以及新提出的两种基于局部随机游走的指标。
1.平均通勤时间(average commute time)简称ACT。其数值解可通过求该网络拉普拉斯矩阵的伪逆 获得
伪逆矩阵:伪逆矩阵是逆矩阵的广义形式。matlab里可以用函数pinv(A)求其伪逆矩阵。函数返回一个与A的转置矩阵A' 同型的矩阵X,并且满足:AXA=A,XAX=X.也称为广义逆矩阵。pinv(A)具有inv(A)的部分特性
2.基于随机游走的余弦相似性
3.重启的随机游走(random walk with restart)简称RWR 。该指标可以看成是网页排序算法(PageRank)的拓展应用,设随机游走粒子每走一步时都以一定概率返回初始位置。设粒子返回概率为1−c
4. SimRank指标简称SimR。它的基本假设是,如果两节点所连接的节点相似,则该两节点相似,同时考虑了结构等价和一般等价。描述了两个分别从节点和出发的粒子平均过多久会相遇。
3.3.2 局部随机游走
基于全局的随机游走指标往往随机复杂度很高,因此很难在大规模网络上实际应用,局部只考虑有限步数的游走过程。
1.局部随机游走指标
2.叠加的局部随机游走指标目的就是给邻近目标节点的点更多的机会与目标节点相连,充分考虑了很多真是网络连接上的局域性特点。
3.6预测效果比较
3.6.1 实验数据
1.美国航空网络USAir(无向无权,322/2126) 2.科学家合作网络NS(含权,1589/268/379) 3.政治博客网络PB (1224/19022,1222/19021) 4.蛋白质相互作用网络Yeast (2617/11855,2375,90.75%) 5.线虫神经网络C.elegans(297/2148) 6.食物链网络FWFB (128/2106) 7.电力网络Power(4941/6594) 8.路由器网络Router(该网络非常稀疏,5022/6258)
P76表2给出了算法在8个真实网络中的预测,精确性用AUC衡量,网络测试集与训练集的划分比例为1:9, 即测试集包含10牦的边。从表2可以看出,全局指标普遍表现比只利用最近邻信息的局部指标好一些,但是利用了最近邻和次近邻的局部路径指标LP表现已经和全局指标不相上下。全局指标中RWR、Cos+和Katz表现特别突出。 只利用最近邻的指标中,RA表现最为抢眼,AA次之,说明惩罚大度的共同邻居确实可以起到作用,这一思想在局部朴素贝叶斯方法中得到了淋漓尽致的展 现,此方法的确能够将精确性再推进一步。对比网络结构特征参考附录B, 我们还可以发现网络结构对于指标的选择有重要影响,譬如说只考虑最近邻的局部指标往往只在网络簇系数很大的时候才会有良好表现,又譬如基于共同邻居的转移相似性指标TSCN对于Router网络和Power网络有非常好的表现,是因为这些网络连接密度低,而在其他情况则可能表现平平。
四、基于似然分析的链路预测
最复杂的一种框架,远远复杂于基于节点相似性,而且框架中每一个组成成分都非常复杂,不是一个应用性很强的方法,但是给出了我们对于网络结构的深刻洞见。
4.1层次结构模型HSM
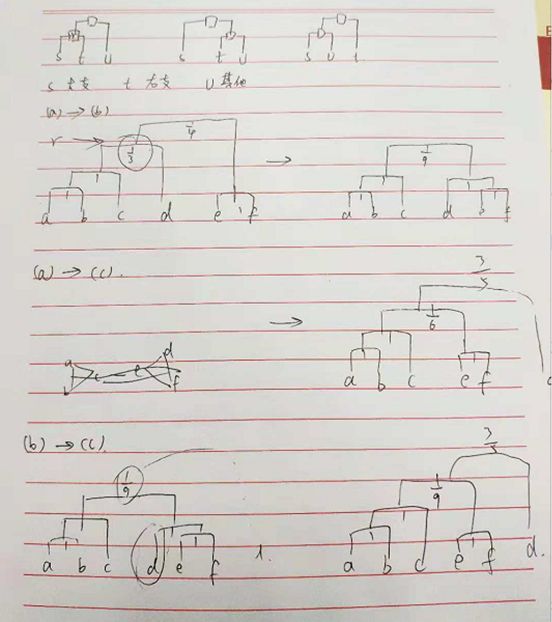
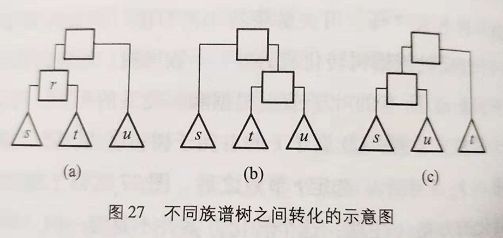
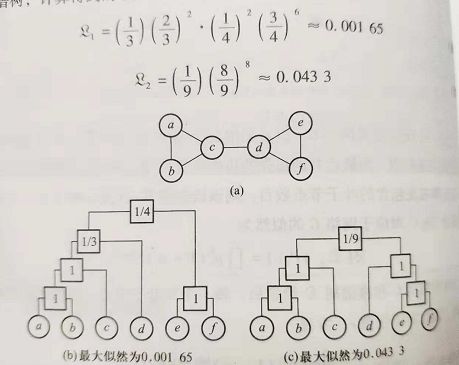
含有 N 个节点的网络可以由一个含有 N 个叶子节点和 N−1 个内部节点的树状图表示
对于有明显层次结构的网络表现尚好,如恐怖袭击网络和草原食物链网络,而对于层次结构不明显的网络,如科学家合作网和线虫神经网络,表现还不如最简单的共同邻居算法
不同族谱树之间转化
4.2随机分块模型
网络中的节点分成若干个群,两个节点是否连接的概率只取决于节点所在的群,同一个群中所有结点的地位是相同的
适合刻画节点所属群的成员身份对于连接行为有关键影响的情况
由两部分信息决定,一是网络被分成若干群的方案,二是分属于两个群的两点之间产生连边的概率矩阵
该方法在精确性的表现上,要略好与层次结构模型
4.3闭路模型
先根据网络结构形成的某项或某些驱动因素定义网络的,哈密顿量,一条未被观察到的边存在的可能性可以用添加这条边后网络的似然来衡量
网络结构形成种特别重要的一个驱动,因素是局部性原则,该原则认为有很多共同邻居或者至少在网络中距离很近的节点之间更容易产生新的连边
符合局部性原则的网络会有很高密度的低阶环,其中三阶环的多少,直接决定了网络簇系数的大小,共同邻居相似性良好的表现背后是因为网络形成的时候,更青睐三阶环
小结
从表三和表四可以看出随机分块模型的效果,要好与层次结构模型,而与相似性指标的结果在不同网络和不同精确性测度的表现各有千秋但是这些方法的精确性不论用AUC,还是precision度量都不如闭路模型精确
似然分析的思路在数学上非常优雅,预测结果也相当不错,还可以通过参数的拟合和构型的抽样结果,得到一些关于网络结构的额外信息,共同缺点是计算量大,往往几千上万的节点就会带来很大的负担,目前尚无法用来处理大规模网络
五.加权网络的链路预测
首先介绍刻画加权网络的一般方法和指标,讨论加权网络上的动力学,然后给出若干有代表性的加权网络链路预测的方法
5.1加权网络
5.1.1图表示
可以用一个邻接矩阵表示,矩阵中的元素表示的是权重,无向加权网络的邻接矩阵是对称的,这和无向无权网络的邻接矩阵是一致的,注意节点标号的顺序并不会改变邻接矩阵的性质,参见矩阵的正交相似变换
5.1.2刻画加权网络
1.边的长度,与权重相关
①相异权:权重越大,两个接点越远离越不亲密
②相似权:权重越大两个节点越亲近越亲密
⒉路径长度:m-1条边长度之和
⒊平均距离,网络平均距离定义为网络中所有节点队之间距离的平均值。所有路径中长度最短的路径称为两节点之间的测地线
⒋度分布和强度分布:节点的强度定义为与该节点连接的所有边的权重之和。真实加权网络的,节点度分布节点强度分布边权分布往往都是胖尾的,可以用幂率函数近似刻画
⒌簇系数:
⒍模体:网络重要的局部结构,指网络中出现频率特别高的连通子图
⒎群落结构:群落结构划分的效果可以用模块度来衡量。在无权网络中,只需要把优化的目标函数改成含权形势,即可应用于加权网络的群落划分。
5.1.3加权网络上的动力学
权重对于网络的功能有很大影响,有目的的加权可以干预甚至优化网络中的动力学
对SI、SIS传播模型研究显示,权重分布越均匀传播速度越快;
对SIR研究显示,一条边的权重与这条边两个端点度乘积的关联方式对于传播的阈值和波及范围都有重大影响
常见的是将一条边的权重定义为两端点度乘积的某个幂次
5.2加权网络的相似性与链路预测
5.2.1加权相似性指标
含权的CN指标、AA、RA、PA、基于路径的含权相似性、随机游走的相似性
5.2.2预测效果
含权指标的预测效果要好于无权的预测方法,实验中看到,权重在链路预测中起到了正面的作用
*一些研究人员也发现了不用结果,联想到弱连接效应
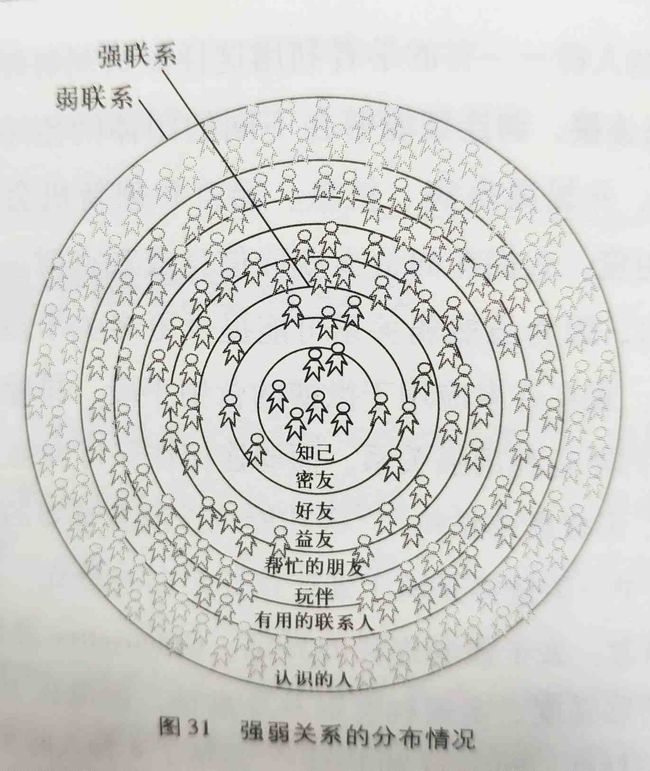
5.3链路预测中的弱连接效应
越是亲密的朋友越是帮不上太大的忙
强连接关系通常代表着行动者彼此之间具有高度的互动,因此通过强连接产生的信息通常是重复的,容易自成一个封闭的系统,因此在组织中并不是一个可以提供创新机会的优良通道
弱连接能够在不同的团体间传递非重复的信息,给团体带来新的机会
弱连接虽然不如强连接那样坚固,却有着极快的、可能具有低成本和高效能的传播特点
强弱的界定:互动时间、情感强度、亲密程度、互惠性
测量方面可以按照边的权重从小到大进行排序,前p比例的为弱连接,后1-p为强连接
强连接更优先产生于拥有重叠邻居的节点之间,产生于社群内部。
为了进一步研究网络中强弱链接对于链路预测的作用,原有指标引入参数α来调节权重作用,得到含参的含权CN,AA和RA相似指标
六.有向网络的链路预测
存在不对称关联或单向连接的网络就是有向网络。注意无向网络中最大边数M是N(N-1)/2,而有向网络中M为N(N-1)。
图表示:节点集合和有向边集合表示;(三个条件:连边有方向,不存在某点同时为始点终点,两点间最多一条连边。)
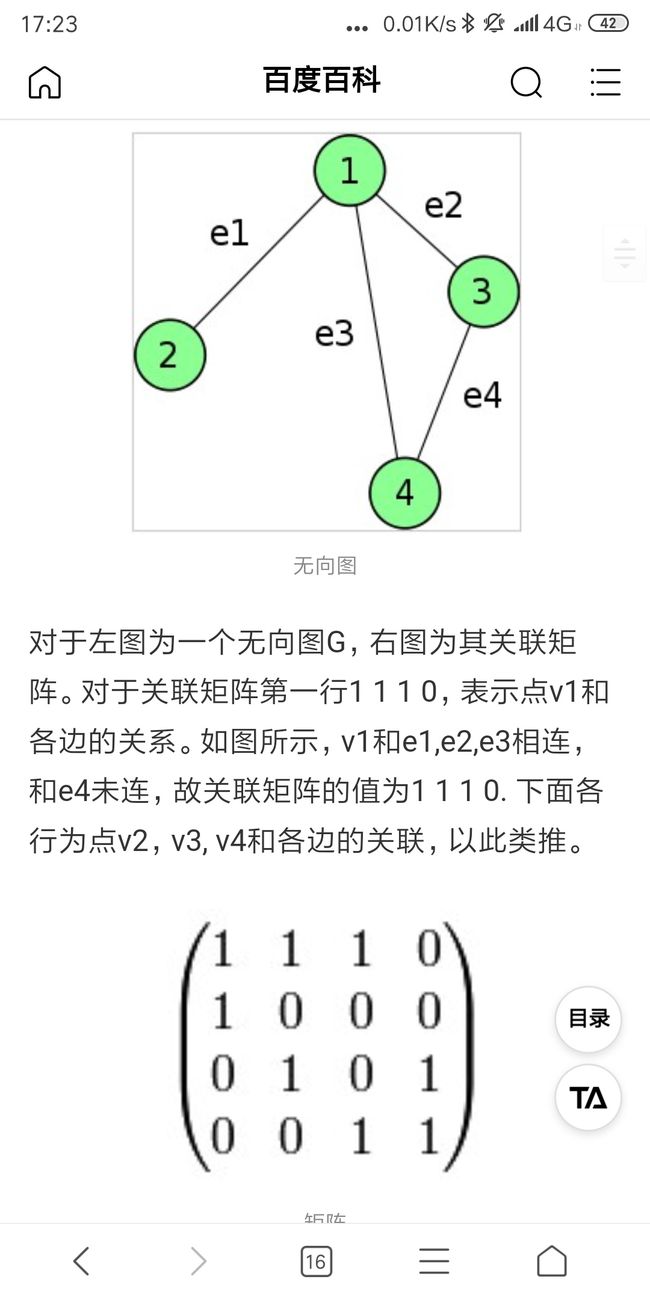
这时网络的邻接矩阵是不对称的啊,另外还可用关联矩阵来刻画网络。邻接矩阵表示的是节点节点之间的关系,关联矩阵表示的是节点连边之间的关系
关联矩阵
需要注意的一点,每一行值的总和为该点的度。
对于有向图,若bij = 1,表示边j离开点i。 若bij = -1, 表示边j进入点i。 若bij = 0,表示边j和点i不相关联。或者说第i行中“-1”的数目为节点i的入度,“1”的数目为节点i的出度。